M$^3$-Impute: Mask-guided Representation Learning for Missing Value Imputation

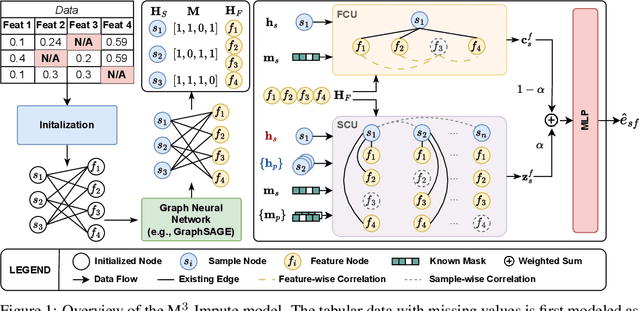
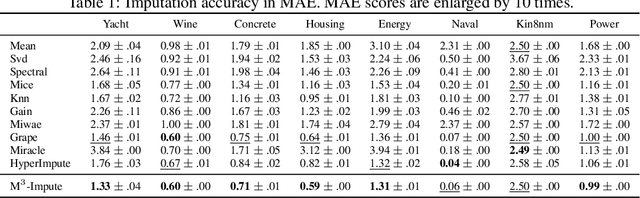
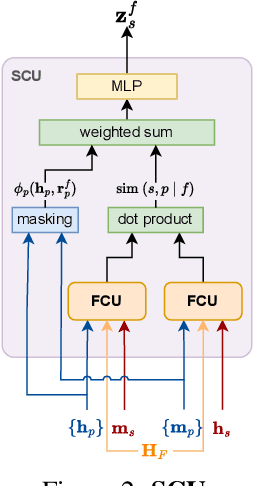
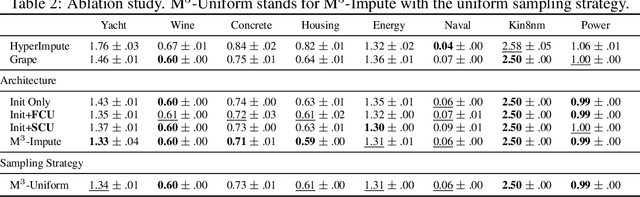
Missing values are a common problem that poses significant challenges to data analysis and machine learning. This problem necessitates the development of an effective imputation method to fill in the missing values accurately, thereby enhancing the overall quality and utility of the datasets. Existing imputation methods, however, fall short of explicitly considering the `missingness' information in the data during the embedding initialization stage and modeling the entangled feature and sample correlations during the learning process, thus leading to inferior performance. We propose M$^3$-Impute, which aims to explicitly leverage the missingness information and such correlations with novel masking schemes. M$^3$-Impute first models the data as a bipartite graph and uses a graph neural network to learn node embeddings, where the refined embedding initialization process directly incorporates the missingness information. They are then optimized through M$^3$-Impute's novel feature correlation unit (FRU) and sample correlation unit (SRU) that effectively captures feature and sample correlations for imputation. Experiment results on 25 benchmark datasets under three different missingness settings show the effectiveness of M$^3$-Impute by achieving 20 best and 4 second-best MAE scores on average.

A Multi-Scale Decomposition MLP-Mixer for Time Series Analysis

Time series data, often characterized by unique composition and complex multi-scale temporal variations, requires special consideration of decomposition and multi-scale modeling in its analysis. Existing deep learning methods on this best fit to only univariate time series, and have not sufficiently accounted for sub-series level modeling and decomposition completeness. To address this, we propose MSD-Mixer, a Multi-Scale Decomposition MLP-Mixer which learns to explicitly decompose the input time series into different components, and represents the components in different layers. To handle multi-scale temporal patterns and inter-channel dependencies, we propose a novel temporal patching approach to model the time series as multi-scale sub-series, i.e., patches, and employ MLPs to mix intra- and inter-patch variations and channel-wise correlations. In addition, we propose a loss function to constrain both the magnitude and autocorrelation of the decomposition residual for decomposition completeness. Through extensive experiments on various real-world datasets for five common time series analysis tasks (long- and short-term forecasting, imputation, anomaly detection, and classification), we demonstrate that MSD-Mixer consistently achieves significantly better performance in comparison with other state-of-the-art task-general and task-specific approaches.

A Lightweight and Accurate Spatial-Temporal Transformer for Traffic Forecasting

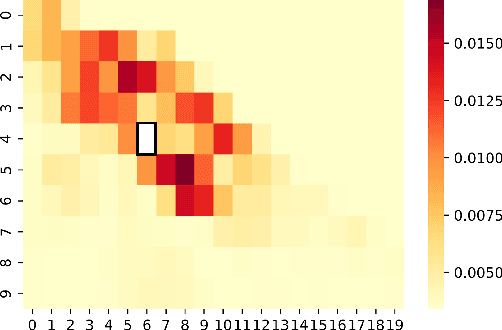
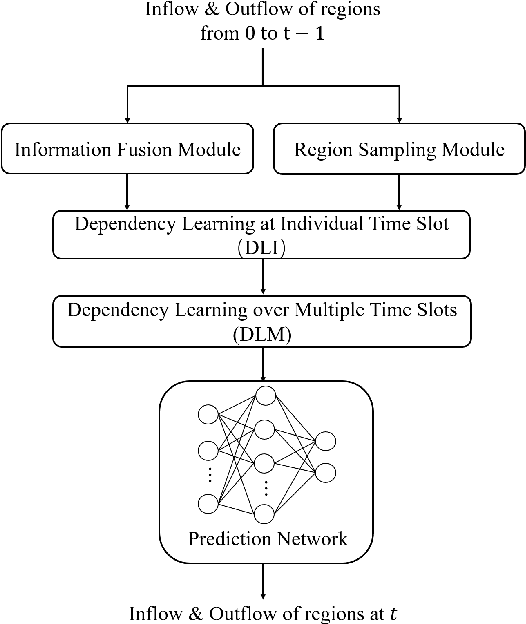
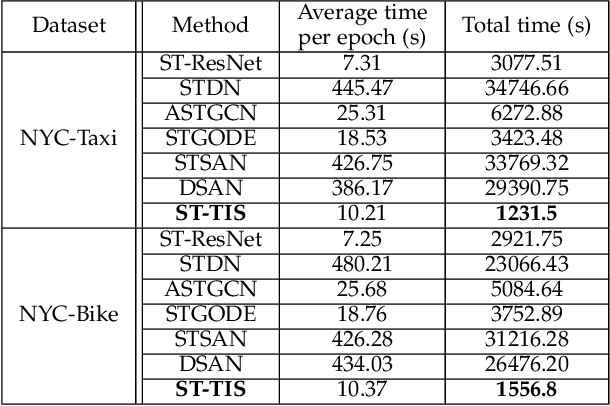
We study the forecasting problem for traffic with dynamic, possibly periodical, and joint spatial-temporal dependency between regions. Given the aggregated inflow and outflow traffic of regions in a city from time slots 0 to t-1, we predict the traffic at time t at any region. Prior arts in the area often consider the spatial and temporal dependencies in a decoupled manner or are rather computationally intensive in training with a large number of hyper-parameters to tune. We propose ST-TIS, a novel, lightweight, and accurate Spatial-Temporal Transformer with information fusion and region sampling for traffic forecasting. ST-TIS extends the canonical Transformer with information fusion and region sampling. The information fusion module captures the complex spatial-temporal dependency between regions. The region sampling module is to improve the efficiency and prediction accuracy, cutting the computation complexity for dependency learning from $O(n^2)$ to $O(n\sqrt{n})$, where n is the number of regions. With far fewer parameters than state-of-the-art models, the offline training of our model is significantly faster in terms of tuning and computation (with a reduction of up to $90\%$ on training time and network parameters). Notwithstanding such training efficiency, extensive experiments show that ST-TIS is substantially more accurate in online prediction than state-of-the-art approaches (with an average improvement of up to $9.5\%$ on RMSE, and $12.4\%$ on MAPE).