M$^3$-Impute: Mask-guided Representation Learning for Missing Value Imputation
Paper and Code
Oct 11, 2024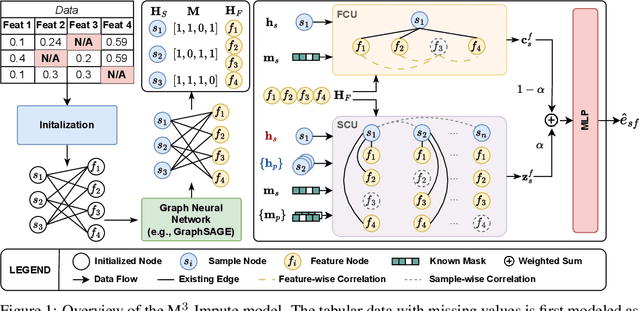
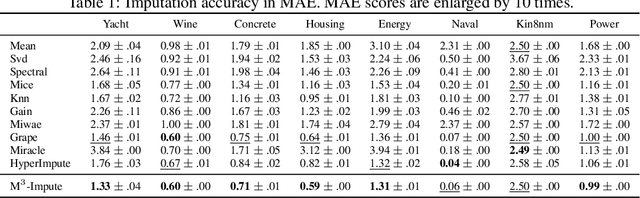
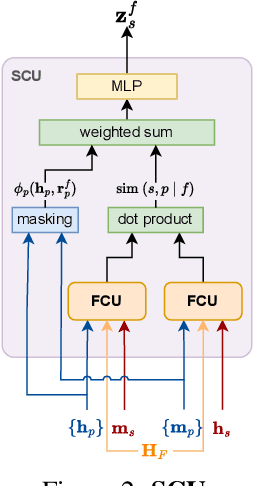
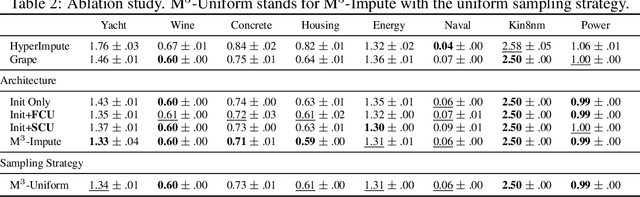
Missing values are a common problem that poses significant challenges to data analysis and machine learning. This problem necessitates the development of an effective imputation method to fill in the missing values accurately, thereby enhancing the overall quality and utility of the datasets. Existing imputation methods, however, fall short of explicitly considering the `missingness' information in the data during the embedding initialization stage and modeling the entangled feature and sample correlations during the learning process, thus leading to inferior performance. We propose M$^3$-Impute, which aims to explicitly leverage the missingness information and such correlations with novel masking schemes. M$^3$-Impute first models the data as a bipartite graph and uses a graph neural network to learn node embeddings, where the refined embedding initialization process directly incorporates the missingness information. They are then optimized through M$^3$-Impute's novel feature correlation unit (FRU) and sample correlation unit (SRU) that effectively captures feature and sample correlations for imputation. Experiment results on 25 benchmark datasets under three different missingness settings show the effectiveness of M$^3$-Impute by achieving 20 best and 4 second-best MAE scores on average.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge