A State Transition Model for Mobile Notifications via Survival Analysis

Mobile notifications have become a major communication channel for social networking services to keep users informed and engaged. As more mobile applications push notifications to users, they constantly face decisions on what to send, when and how. A lack of research and methodology commonly leads to heuristic decision making. Many notifications arrive at an inappropriate moment or introduce too many interruptions, failing to provide value to users and spurring users' complaints. In this paper we explore unique features of interactions between mobile notifications and user engagement. We propose a state transition framework to quantitatively evaluate the effectiveness of notifications. Within this framework, we develop a survival model for badging notifications assuming a log-linear structure and a Weibull distribution. Our results show that this model achieves more flexibility for applications and superior prediction accuracy than a logistic regression model. In particular, we provide an online use case on notification delivery time optimization to show how we make better decisions, drive more user engagement, and provide more value to users.

On Multiplicative Multitask Feature Learning

We investigate a general framework of multiplicative multitask feature learning which decomposes each task's model parameters into a multiplication of two components. One of the components is used across all tasks and the other component is task-specific. Several previous methods have been proposed as special cases of our framework. We study the theoretical properties of this framework when different regularization conditions are applied to the two decomposed components. We prove that this framework is mathematically equivalent to the widely used multitask feature learning methods that are based on a joint regularization of all model parameters, but with a more general form of regularizers. Further, an analytical formula is derived for the across-task component as related to the task-specific component for all these regularizers, leading to a better understanding of the shrinkage effect. Study of this framework motivates new multitask learning algorithms. We propose two new learning formulations by varying the parameters in the proposed framework. Empirical studies have revealed the relative advantages of the two new formulations by comparing with the state of the art, which provides instructive insights into the feature learning problem with multiple tasks.

Coarse-to-Fine Classification via Parametric and Nonparametric Models for Computer-Aided Diagnosis

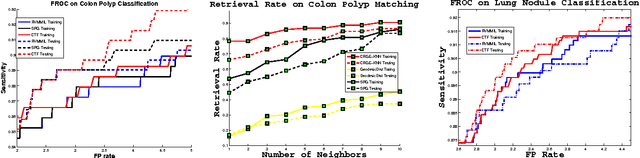
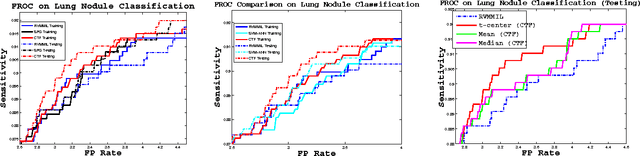
Classification is one of the core problems in Computer-Aided Diagnosis (CAD), targeting for early cancer detection using 3D medical imaging interpretation. High detection sensitivity with desirably low false positive (FP) rate is critical for a CAD system to be accepted as a valuable or even indispensable tool in radiologists' workflow. Given various spurious imagery noises which cause observation uncertainties, this remains a very challenging task. In this paper, we propose a novel, two-tiered coarse-to-fine (CTF) classification cascade framework to tackle this problem. We first obtain classification-critical data samples (e.g., samples on the decision boundary) extracted from the holistic data distributions using a robust parametric model (e.g., \cite{Raykar08}); then we build a graph-embedding based nonparametric classifier on sampled data, which can more accurately preserve or formulate the complex classification boundary. These two steps can also be considered as effective "sample pruning" and "feature pursuing + $k$NN/template matching", respectively. Our approach is validated comprehensively in colorectal polyp detection and lung nodule detection CAD systems, as the top two deadly cancers, using hospital scale, multi-site clinical datasets. The results show that our method achieves overall better classification/detection performance than existing state-of-the-art algorithms using single-layer classifiers, such as the support vector machine variants \cite{Wang08}, boosting \cite{Slabaugh10}, logistic regression \cite{Ravesteijn10}, relevance vector machine \cite{Raykar08}, $k$-nearest neighbor \cite{Murphy09} or spectral projections on graph \cite{Cai08}.