On Multi-Fidelity Impedance Tuning for Human-Robot Cooperative Manipulation

We examine how a human-robot interaction (HRI) system may be designed when input-output data from previous experiments are available. In particular, we consider how to select an optimal impedance in the assistance design for a cooperative manipulation task with a new operator. Due to the variability between individuals, the design parameters that best suit one operator of the robot may not be the best parameters for another one. However, by incorporating historical data using a linear auto-regressive (AR-1) Gaussian process, the search for a new operator's optimal parameters can be accelerated. We lay out a framework for optimizing the human-robot cooperative manipulation that only requires input-output data. We establish how the AR-1 model improves the bound on the regret and numerically simulate a human-robot cooperative manipulation task to show the regret improvement. Further, we show how our approach's input-output nature provides robustness against modeling error through an additional numerical study.

Automated Adversary Emulation for Cyber-Physical Systems via Reinforcement Learning

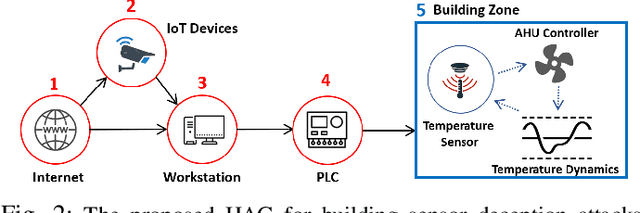
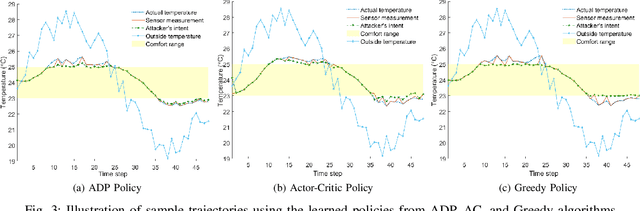
Adversary emulation is an offensive exercise that provides a comprehensive assessment of a system's resilience against cyber attacks. However, adversary emulation is typically a manual process, making it costly and hard to deploy in cyber-physical systems (CPS) with complex dynamics, vulnerabilities, and operational uncertainties. In this paper, we develop an automated, domain-aware approach to adversary emulation for CPS. We formulate a Markov Decision Process (MDP) model to determine an optimal attack sequence over a hybrid attack graph with cyber (discrete) and physical (continuous) components and related physical dynamics. We apply model-based and model-free reinforcement learning (RL) methods to solve the discrete-continuous MDP in a tractable fashion. As a baseline, we also develop a greedy attack algorithm and compare it with the RL procedures. We summarize our findings through a numerical study on sensor deception attacks in buildings to compare the performance and solution quality of the proposed algorithms.

Secure Route Planning Using Dynamic Games with Stopping States

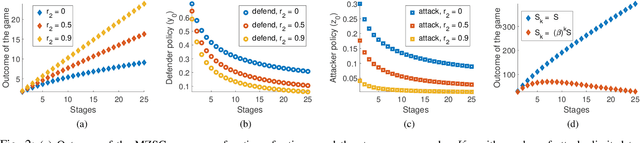
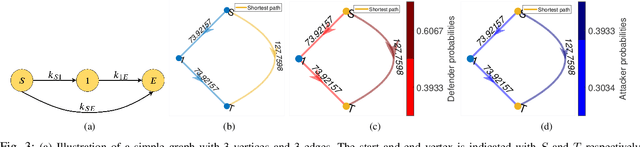
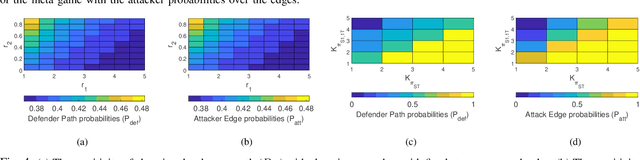
We consider the classic motion planning problem defined over a roadmap in which a vehicle seeks to find an optimal path to a given destination from a given starting location in presence of an attacker who can launch attacks on the vehicle over any edge of the roadmap. The vehicle (defender) has the capability to switch on/off a countermeasure that can detect and permanently disable the attack if it occurs concurrently. We model this problem using the framework of a zero-sum dynamic game with a stopping state being played simultaneously by the two players. We characterize the Nash equilibria of this game and provide closed form expressions for the case of two actions per player. We further provide an analytic lower bound on the value of the game and characterize conditions under which it grows sub-linearly with the number of stages. We then study the sensitivity of the Nash equilibrium to (i) the cost of using the countermeasure, (ii) the cost of motion and (iii) the benefit of disabling the attack. We then apply these results to solve the motion planning problem and compare the benefit of our approach over a competing approach based on converting the problem to a shortest path problem using the expected cost of playing the game over each edge.

Sequential Randomized Matrix Factorization for Gaussian Processes: Efficient Predictions and Hyper-parameter Optimization

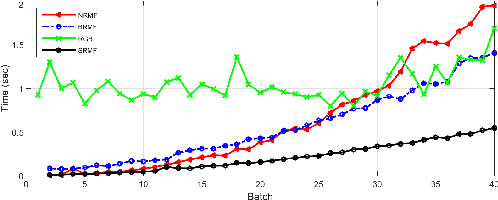
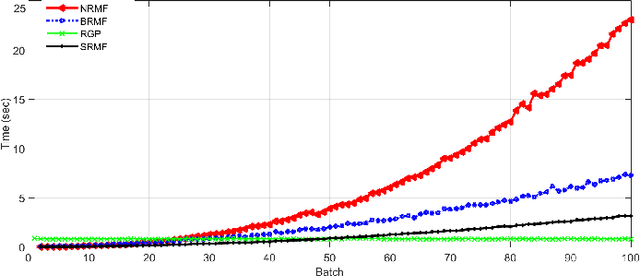
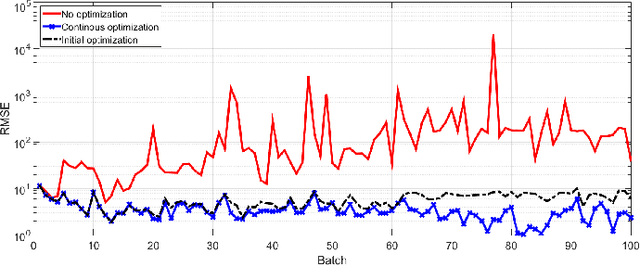
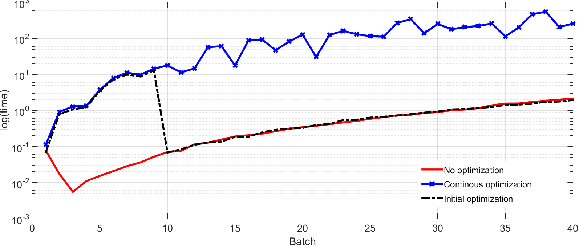
This paper presents a sequential randomized lowrank matrix factorization approach for incrementally predicting values of an unknown function at test points using the Gaussian Processes framework. It is well-known that in the Gaussian processes framework, the computational bottlenecks are the inversion of the (regularized) kernel matrix and the computation of the hyper-parameters defining the kernel. The main contributions of this paper are two-fold. First, we formalize an approach to compute the inverse of the kernel matrix using randomized matrix factorization algorithms in a streaming scenario, i.e., data is generated incrementally over time. The metrics of accuracy and computational efficiency of the proposed method are compared against a batch approach based on use of randomized matrix factorization and an existing streaming approach based on approximating the Gaussian process by a finite set of basis vectors. Second, we extend the sequential factorization approach to a class of kernel functions for which the hyperparameters can be efficiently optimized. All results are demonstrated on two publicly available datasets.

Robust Belief Roadmap: Planning Under Intermittent Sensing

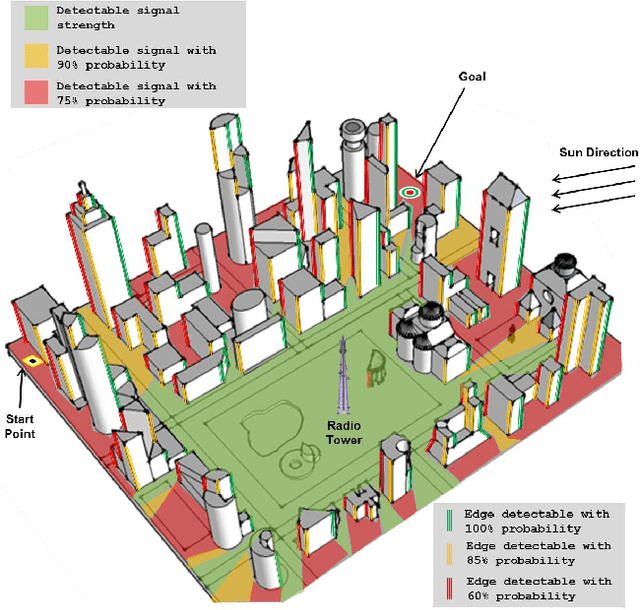
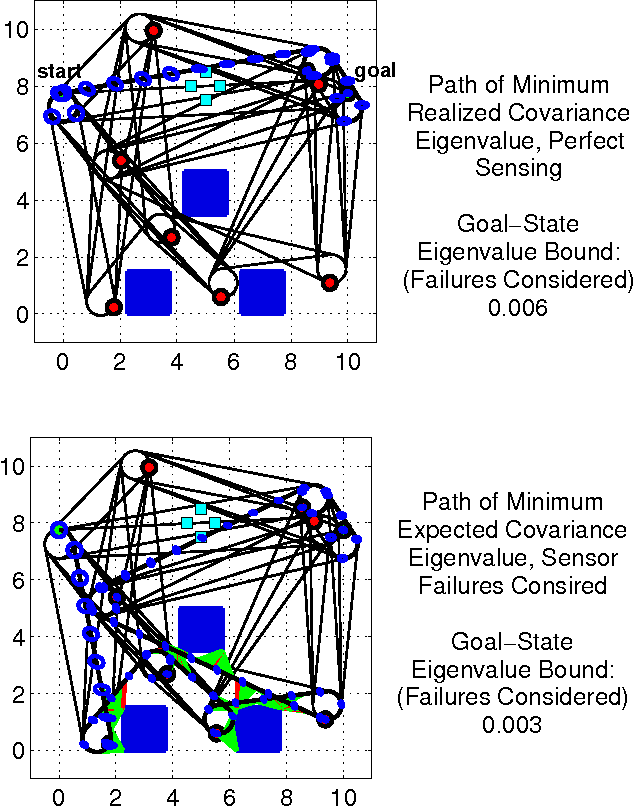
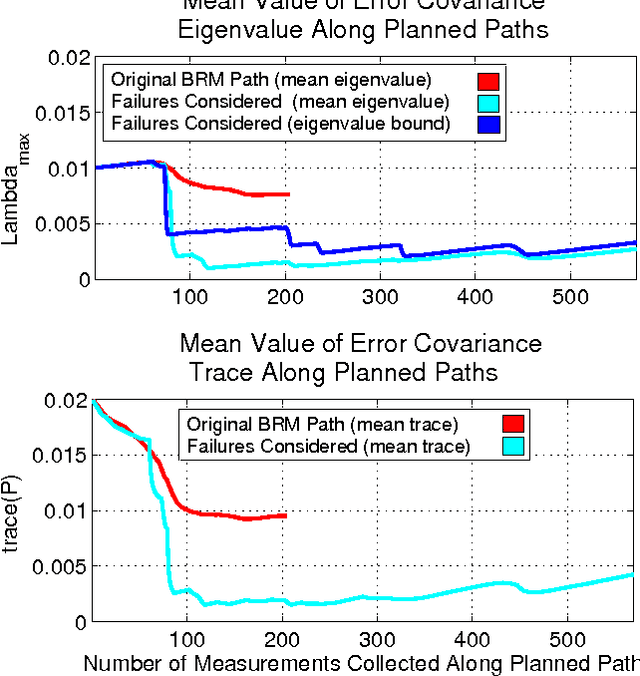
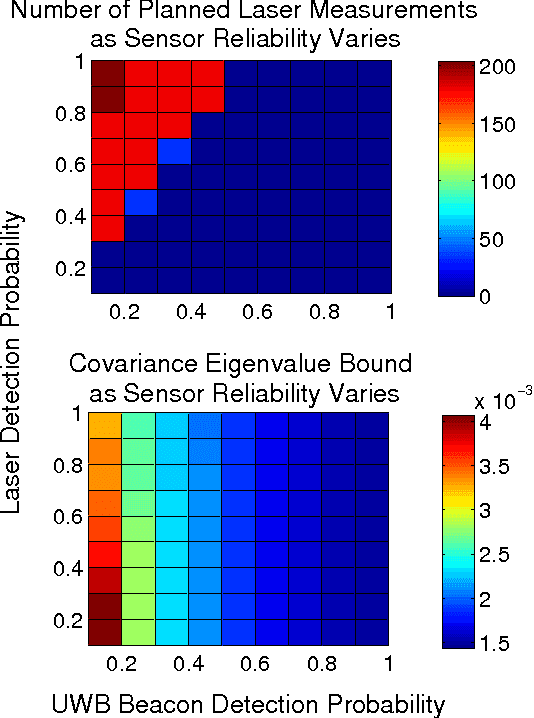
In this paper, we extend the recent body of work on planning under uncertainty to include the fact that sensors may not provide any measurement owing to misdetection. This is caused either by adverse environmental conditions that prevent the sensors from making measurements or by the fundamental limitations of the sensors. Examples include RF-based ranging devices that intermittently do not receive the signal from beacons because of obstacles; the misdetection of features by a camera system in detrimental lighting conditions; a LIDAR sensor that is pointed at a glass-based material such as a window, etc. The main contribution of this paper is twofold. We first show that it is possible to obtain an analytical bound on the performance of a state estimator under sensor misdetection occurring stochastically over time in the environment. We then show how this bound can be used in a sample-based path planning algorithm to produce a path that trades off accuracy and robustness. Computational results demonstrate the benefit of the approach and comparisons are made with the state of the art in path planning under state uncertainty.

A Dynamic Boundary Guarding Problem with Translating Targets

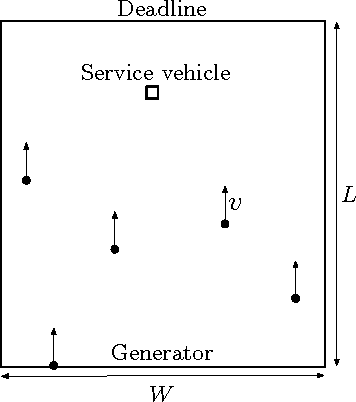
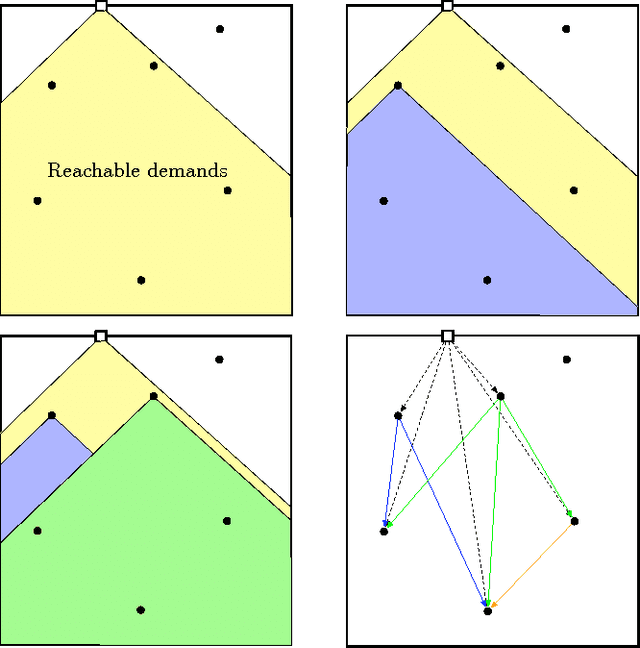
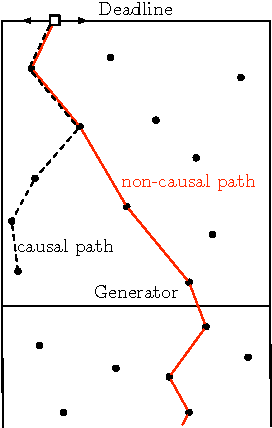
We introduce a problem in which a service vehicle seeks to guard a deadline (boundary) from dynamically arriving mobile targets. The environment is a rectangle and the deadline is one of its edges. Targets arrive continuously over time on the edge opposite the deadline, and move towards the deadline at a fixed speed. The goal for the vehicle is to maximize the fraction of targets that are captured before reaching the deadline. We consider two cases; when the service vehicle is faster than the targets, and; when the service vehicle is slower than the targets. In the first case we develop a novel vehicle policy based on computing longest paths in a directed acyclic graph. We give a lower bound on the capture fraction of the policy and show that the policy is optimal when the distance between the target arrival edge and deadline becomes very large. We present numerical results which suggest near optimal performance away from this limiting regime. In the second case, when the targets are slower than the vehicle, we propose a policy based on servicing fractions of the translational minimum Hamiltonian path. In the limit of low target speed and high arrival rate, the capture fraction of this policy is within a small constant factor of the optimal.