Distributionally Robust Imitation Learning: Layered Control Architecture for Certifiable Autonomy

Imitation learning (IL) enables autonomous behavior by learning from expert demonstrations. While more sample-efficient than comparative alternatives like reinforcement learning, IL is sensitive to compounding errors induced by distribution shifts. There are two significant sources of distribution shifts when using IL-based feedback laws on systems: distribution shifts caused by policy error and distribution shifts due to exogenous disturbances and endogenous model errors due to lack of learning. Our previously developed approaches, Taylor Series Imitation Learning (TaSIL) and $\mathcal{L}_1$ -Distributionally Robust Adaptive Control (\ellonedrac), address the challenge of distribution shifts in complementary ways. While TaSIL offers robustness against policy error-induced distribution shifts, \ellonedrac offers robustness against distribution shifts due to aleatoric and epistemic uncertainties. To enable certifiable IL for learned and/or uncertain dynamical systems, we formulate \textit{Distributionally Robust Imitation Policy (DRIP)} architecture, a Layered Control Architecture (LCA) that integrates TaSIL and~\ellonedrac. By judiciously designing individual layer-centric input and output requirements, we show how we can guarantee certificates for the entire control pipeline. Our solution paves the path for designing fully certifiable autonomy pipelines, by integrating learning-based components, such as perception, with certifiable model-based decision-making through the proposed LCA approach.

A Robust Task-Level Control Architecture for Learned Dynamical Systems

Dynamical system (DS)-based learning from demonstration (LfD) is a powerful tool for generating motion plans in the operation (`task') space of robotic systems. However, the realization of the generated motion plans is often compromised by a ''task-execution mismatch'', where unmodeled dynamics, persistent disturbances, and system latency cause the robot's actual task-space state to diverge from the desired motion trajectory. We propose a novel task-level robust control architecture, L1-augmented Dynamical Systems (L1-DS), that explicitly handles the task-execution mismatch in tracking a nominal motion plan generated by any DS-based LfD scheme. Our framework augments any DS-based LfD model with a nominal stabilizing controller and an L1 adaptive controller. Furthermore, we introduce a windowed Dynamic Time Warping (DTW)-based target selector, which enables the nominal stabilizing controller to handle temporal misalignment for improved phase-consistent tracking. We demonstrate the efficacy of our architecture on the LASA and IROS handwriting datasets.

Integrating Vision Systems and STPA for Robust Landing and Take-Off in VTOL Aircraft

Vertical take-off and landing (VTOL) unmanned aerial vehicles (UAVs) are versatile platforms widely used in applications such as surveillance, search and rescue, and urban air mobility. Despite their potential, the critical phases of take-off and landing in uncertain and dynamic environments pose significant safety challenges due to environmental uncertainties, sensor noise, and system-level interactions. This paper presents an integrated approach combining vision-based sensor fusion with System-Theoretic Process Analysis (STPA) to enhance the safety and robustness of VTOL UAV operations during take-off and landing. By incorporating fiducial markers, such as AprilTags, into the control architecture, and performing comprehensive hazard analysis, we identify unsafe control actions and propose mitigation strategies. Key contributions include developing the control structure with vision system capable of identifying a fiducial marker, multirotor controller and corresponding unsafe control actions and mitigation strategies. The proposed solution is expected to improve the reliability and safety of VTOL UAV operations, paving the way for resilient autonomous systems.

Automated Adversary Emulation for Cyber-Physical Systems via Reinforcement Learning

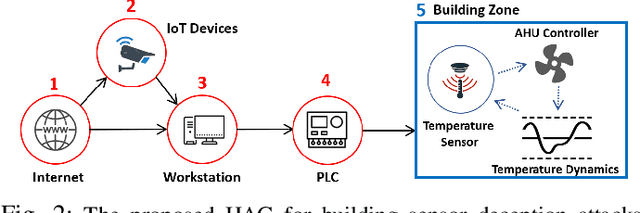
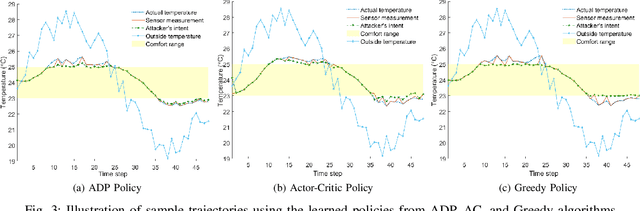
Adversary emulation is an offensive exercise that provides a comprehensive assessment of a system's resilience against cyber attacks. However, adversary emulation is typically a manual process, making it costly and hard to deploy in cyber-physical systems (CPS) with complex dynamics, vulnerabilities, and operational uncertainties. In this paper, we develop an automated, domain-aware approach to adversary emulation for CPS. We formulate a Markov Decision Process (MDP) model to determine an optimal attack sequence over a hybrid attack graph with cyber (discrete) and physical (continuous) components and related physical dynamics. We apply model-based and model-free reinforcement learning (RL) methods to solve the discrete-continuous MDP in a tractable fashion. As a baseline, we also develop a greedy attack algorithm and compare it with the RL procedures. We summarize our findings through a numerical study on sensor deception attacks in buildings to compare the performance and solution quality of the proposed algorithms.

Secure Route Planning Using Dynamic Games with Stopping States

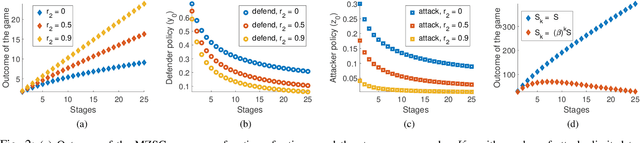
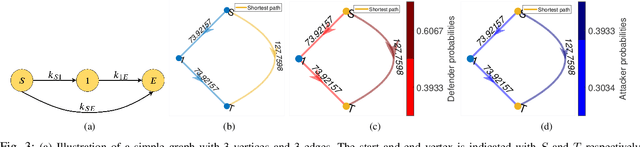
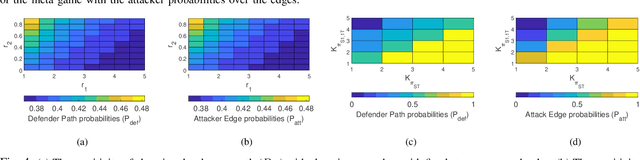
We consider the classic motion planning problem defined over a roadmap in which a vehicle seeks to find an optimal path to a given destination from a given starting location in presence of an attacker who can launch attacks on the vehicle over any edge of the roadmap. The vehicle (defender) has the capability to switch on/off a countermeasure that can detect and permanently disable the attack if it occurs concurrently. We model this problem using the framework of a zero-sum dynamic game with a stopping state being played simultaneously by the two players. We characterize the Nash equilibria of this game and provide closed form expressions for the case of two actions per player. We further provide an analytic lower bound on the value of the game and characterize conditions under which it grows sub-linearly with the number of stages. We then study the sensitivity of the Nash equilibrium to (i) the cost of using the countermeasure, (ii) the cost of motion and (iii) the benefit of disabling the attack. We then apply these results to solve the motion planning problem and compare the benefit of our approach over a competing approach based on converting the problem to a shortest path problem using the expected cost of playing the game over each edge.