Secure Route Planning Using Dynamic Games with Stopping States

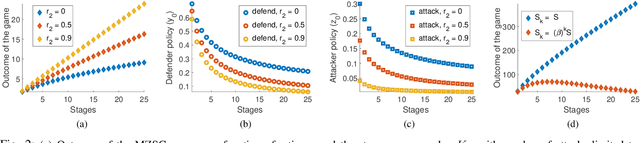
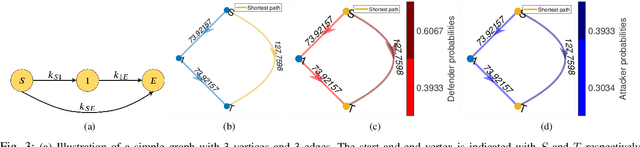
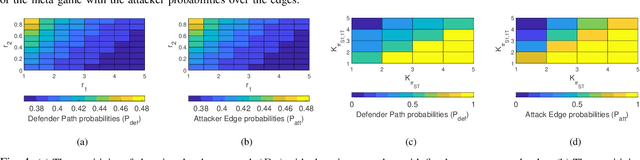
We consider the classic motion planning problem defined over a roadmap in which a vehicle seeks to find an optimal path to a given destination from a given starting location in presence of an attacker who can launch attacks on the vehicle over any edge of the roadmap. The vehicle (defender) has the capability to switch on/off a countermeasure that can detect and permanently disable the attack if it occurs concurrently. We model this problem using the framework of a zero-sum dynamic game with a stopping state being played simultaneously by the two players. We characterize the Nash equilibria of this game and provide closed form expressions for the case of two actions per player. We further provide an analytic lower bound on the value of the game and characterize conditions under which it grows sub-linearly with the number of stages. We then study the sensitivity of the Nash equilibrium to (i) the cost of using the countermeasure, (ii) the cost of motion and (iii) the benefit of disabling the attack. We then apply these results to solve the motion planning problem and compare the benefit of our approach over a competing approach based on converting the problem to a shortest path problem using the expected cost of playing the game over each edge.