George S. Eskander Ekladious
Sequential Randomized Matrix Factorization for Gaussian Processes: Efficient Predictions and Hyper-parameter Optimization
Nov 19, 2017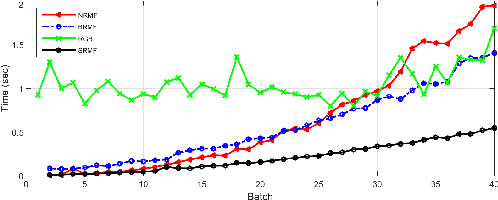
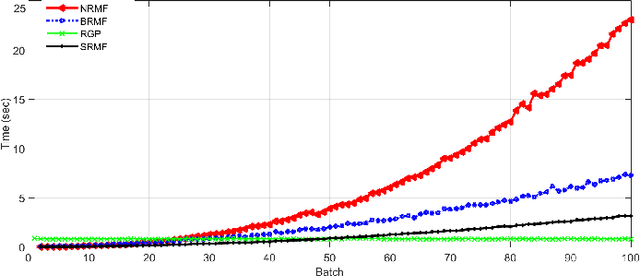
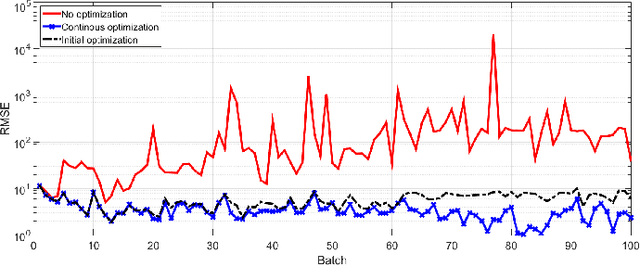
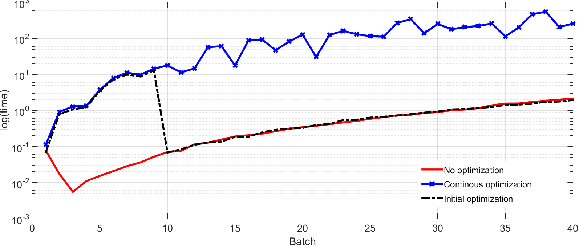
Abstract:This paper presents a sequential randomized lowrank matrix factorization approach for incrementally predicting values of an unknown function at test points using the Gaussian Processes framework. It is well-known that in the Gaussian processes framework, the computational bottlenecks are the inversion of the (regularized) kernel matrix and the computation of the hyper-parameters defining the kernel. The main contributions of this paper are two-fold. First, we formalize an approach to compute the inverse of the kernel matrix using randomized matrix factorization algorithms in a streaming scenario, i.e., data is generated incrementally over time. The metrics of accuracy and computational efficiency of the proposed method are compared against a batch approach based on use of randomized matrix factorization and an existing streaming approach based on approximating the Gaussian process by a finite set of basis vectors. Second, we extend the sequential factorization approach to a class of kernel functions for which the hyperparameters can be efficiently optimized. All results are demonstrated on two publicly available datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge