Shahram Dehdashti
Quantum Cognitively Motivated Decision Fusion for Video Sentiment Analysis
Jan 12, 2021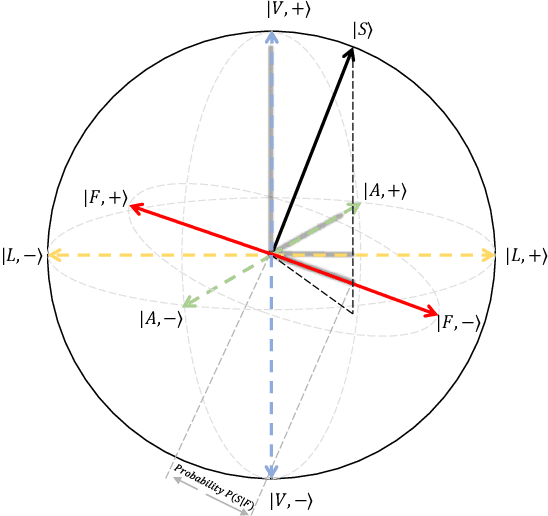
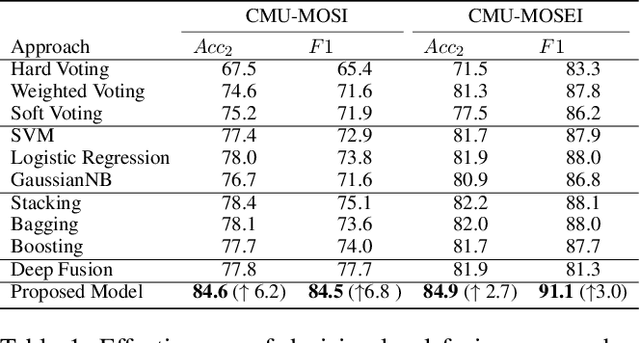
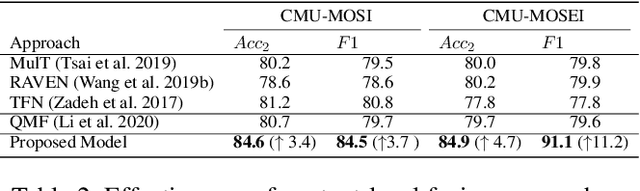
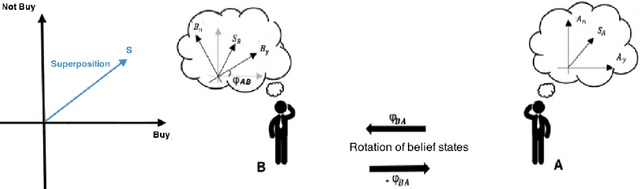
Abstract:Video sentiment analysis as a decision-making process is inherently complex, involving the fusion of decisions from multiple modalities and the so-caused cognitive biases. Inspired by recent advances in quantum cognition, we show that the sentiment judgment from one modality could be incompatible with the judgment from another, i.e., the order matters and they cannot be jointly measured to produce a final decision. Thus the cognitive process exhibits "quantum-like" biases that cannot be captured by classical probability theories. Accordingly, we propose a fundamentally new, quantum cognitively motivated fusion strategy for predicting sentiment judgments. In particular, we formulate utterances as quantum superposition states of positive and negative sentiment judgments, and uni-modal classifiers as mutually incompatible observables, on a complex-valued Hilbert space with positive-operator valued measures. Experiments on two benchmarking datasets illustrate that our model significantly outperforms various existing decision level and a range of state-of-the-art content-level fusion approaches. The results also show that the concept of incompatibility allows effective handling of all combination patterns, including those extreme cases that are wrongly predicted by all uni-modal classifiers.
Kernel Method based on Non-Linear Coherent State
Jul 15, 2020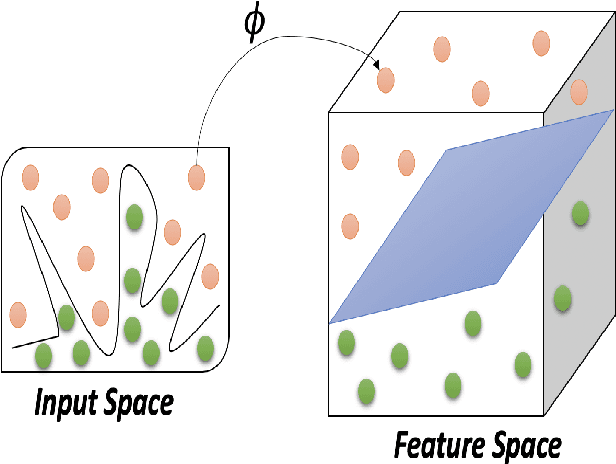
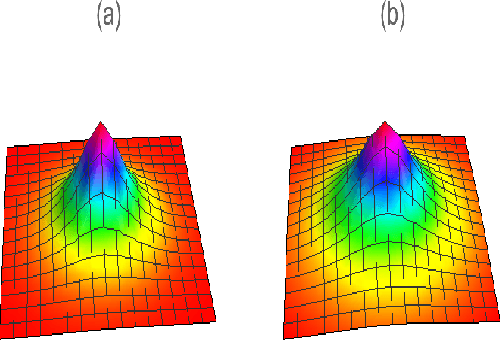
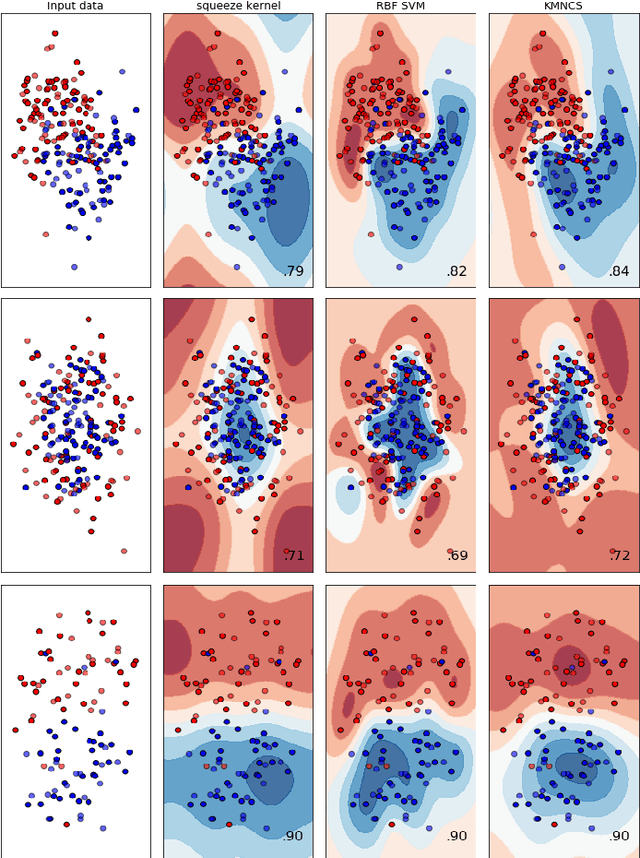
Abstract:In this paper, by mapping datasets to a set of non-linear coherent states, the process of encoding inputs in quantum states as a non-linear feature map is re-interpreted. As a result of this fact that the Radial Basis Function is recovered when data is mapped to a complex Hilbert state represented by coherent states, non-linear coherent states can be considered as natural generalisation of associated kernels. By considering the non-linear coherent states of a quantum oscillator with variable mass, we propose a kernel function based on generalized hypergeometric functions, as orthogonal polynomial functions. The suggested kernel is implemented with support vector machine on two well known datasets (make circles, and make moons) and outperforms the baselines, even in the presence of high noise. In addition, we study impact of geometrical properties of feature space, obtaining by non-linear coherent states, on the SVM classification task, by using considering the Fubini-Study metric of associated coherent states.
Construction of 'Support Vector' Machine Feature Spaces via Deformed Weyl-Heisenberg Algebra
Jun 02, 2020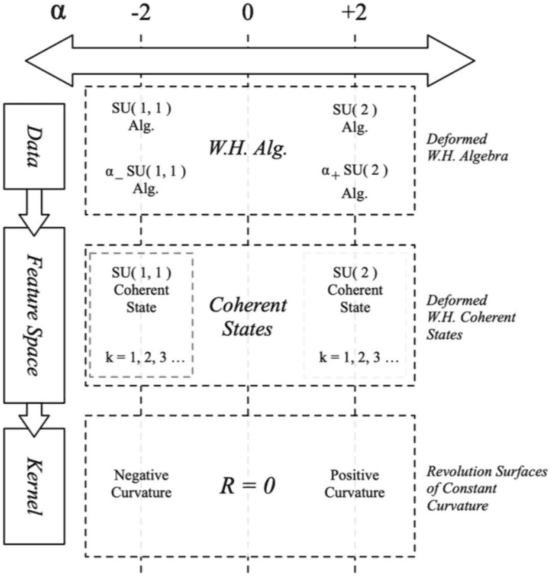



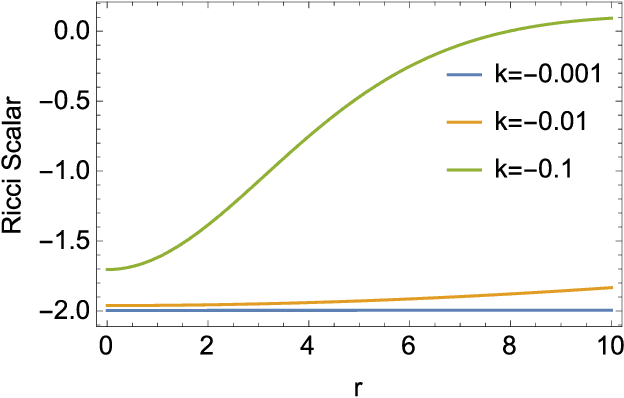
Abstract:This paper uses deformed coherent states, based on a deformed Weyl-Heisenberg algebra that unifies the well-known SU(2), Weyl-Heisenberg, and SU(1,1) groups, through a common parameter. We show that deformed coherent states provide the theoretical foundation of a meta-kernel function, that is a kernel which in turn defines kernel functions. Kernel functions drive developments in the field of machine learning and the meta-kernel function presented in this paper opens new theoretical avenues for the definition and exploration of kernel functions. The meta-kernel function applies associated revolution surfaces as feature spaces identified with non-linear coherent states. An empirical investigation compares the deformed SU(2) and SU(1,1) kernels derived from the meta-kernel which shows performance similar to the Radial Basis kernel, and offers new insights (based on the deformed Weyl-Heisenberg algebra).
Towards a Quantum-Like Cognitive Architecture for Decision-Making
May 11, 2019
Abstract:We propose an alternative and unifying framework for decision-making that, by using quantum mechanics, provides more generalised cognitive and decision models with the ability to represent more information than classical models. This framework can accommodate and predict several cognitive biases reported in Lieder & Griffiths without heavy reliance on heuristics nor on assumptions of the computational resources of the mind.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge