An Extension Of Combinatorial Contextuality For Cognitive Protocols

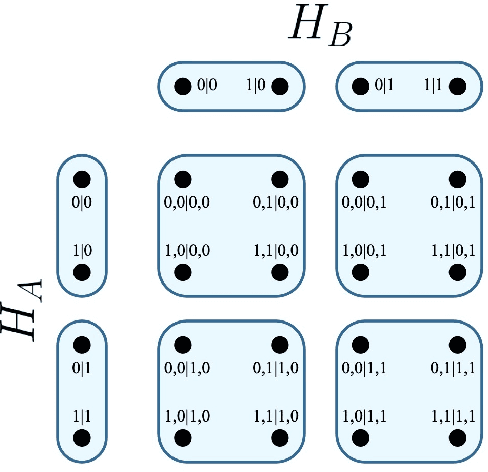
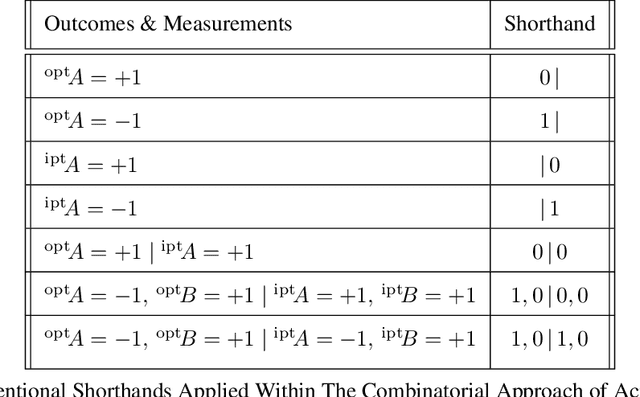
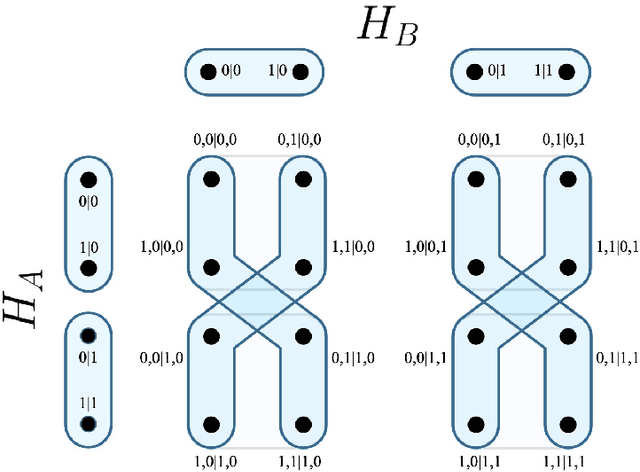
This article extends the combinatorial approach to support the determination of contextuality amidst causal influences. Contextuality is an active field of study in Quantum Cognition, in systems relating to mental phenomena, such as concepts in human memory [Aerts et al., 2013]. In the cognitive field of study, a contemporary challenge facing the determination of whether a phenomenon is contextual has been the identification and management of disturbances [Dzhafarov et al., 2016]. Whether or not said disturbances are identified through the modelling approach, constitute causal influences, or are disregardableas as noise is important, as contextuality cannot be adequately determined in the presence of causal influences [Gleason, 1957]. To address this challenge, we first provide a formalisation of necessary elements of the combinatorial approach within the language of canonical9 causal models. Through this formalisation, we extend the combinatorial approach to support a measurement and treatment of disturbance, and offer techniques to separately distinguish noise and causal influences. Thereafter, we develop a protocol through which these elements may be represented within a cognitive experiment. As human cognition seems rife with causal influences, cognitive modellers may apply the extended combinatorial approach to practically determine the contextuality of cognitive phenomena.

Kernel Method based on Non-Linear Coherent State

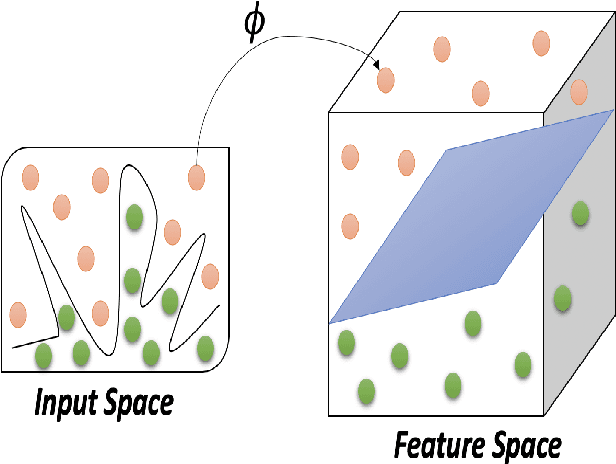
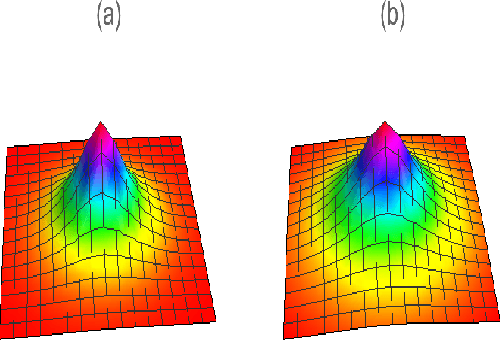
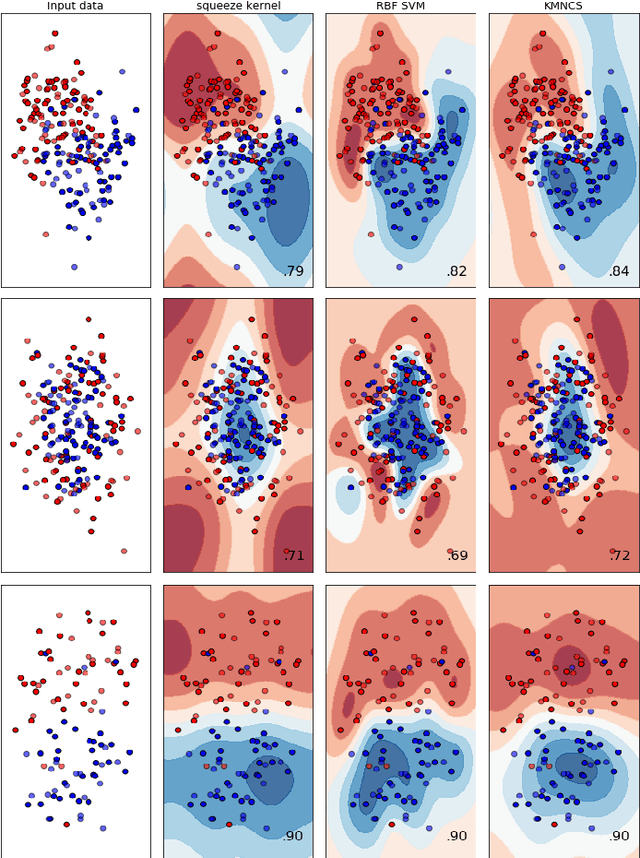
In this paper, by mapping datasets to a set of non-linear coherent states, the process of encoding inputs in quantum states as a non-linear feature map is re-interpreted. As a result of this fact that the Radial Basis Function is recovered when data is mapped to a complex Hilbert state represented by coherent states, non-linear coherent states can be considered as natural generalisation of associated kernels. By considering the non-linear coherent states of a quantum oscillator with variable mass, we propose a kernel function based on generalized hypergeometric functions, as orthogonal polynomial functions. The suggested kernel is implemented with support vector machine on two well known datasets (make circles, and make moons) and outperforms the baselines, even in the presence of high noise. In addition, we study impact of geometrical properties of feature space, obtaining by non-linear coherent states, on the SVM classification task, by using considering the Fubini-Study metric of associated coherent states.

Construction of 'Support Vector' Machine Feature Spaces via Deformed Weyl-Heisenberg Algebra

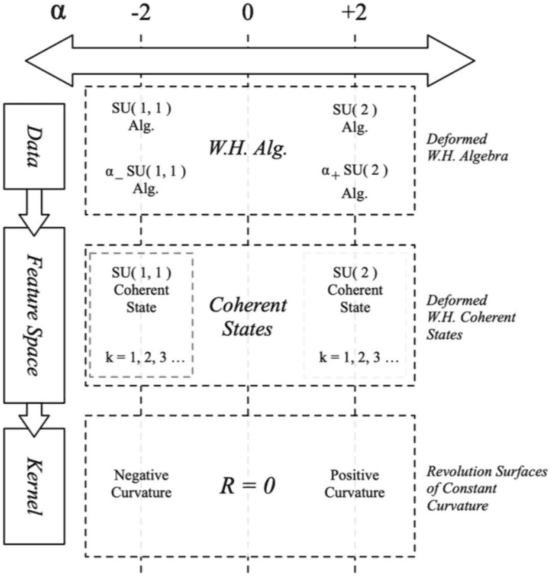
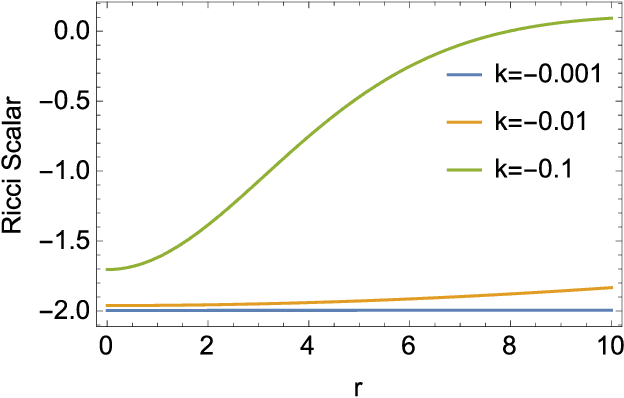
This paper uses deformed coherent states, based on a deformed Weyl-Heisenberg algebra that unifies the well-known SU(2), Weyl-Heisenberg, and SU(1,1) groups, through a common parameter. We show that deformed coherent states provide the theoretical foundation of a meta-kernel function, that is a kernel which in turn defines kernel functions. Kernel functions drive developments in the field of machine learning and the meta-kernel function presented in this paper opens new theoretical avenues for the definition and exploration of kernel functions. The meta-kernel function applies associated revolution surfaces as feature spaces identified with non-linear coherent states. An empirical investigation compares the deformed SU(2) and SU(1,1) kernels derived from the meta-kernel which shows performance similar to the Radial Basis kernel, and offers new insights (based on the deformed Weyl-Heisenberg algebra).