Expanding the class of global objective functions for dissimilarity-based hierarchical clustering

Recent work on dissimilarity-based hierarchical clustering has led to the introduction of global objective functions for this classical problem. Several standard approaches, such as average linkage, as well as some new heuristics have been shown to provide approximation guarantees. Here we introduce a broad new class of objective functions which satisfy desirable properties studied in prior work. Many common agglomerative and divisive clustering methods are shown to be greedy algorithms for these objectives, which are inspired by related concepts in phylogenetics.

Estimating Graph Dimension with Cross-validated Eigenvalues

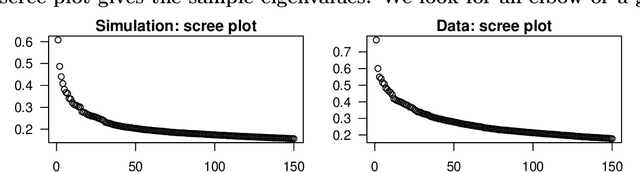
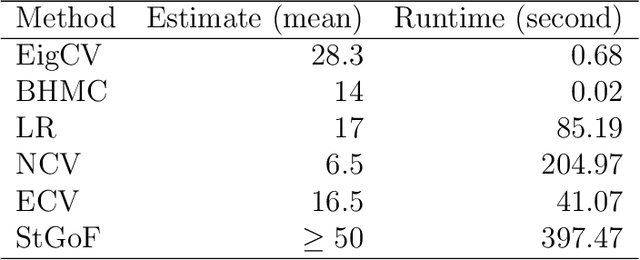
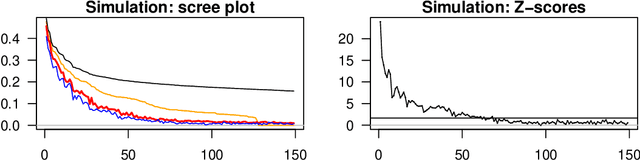
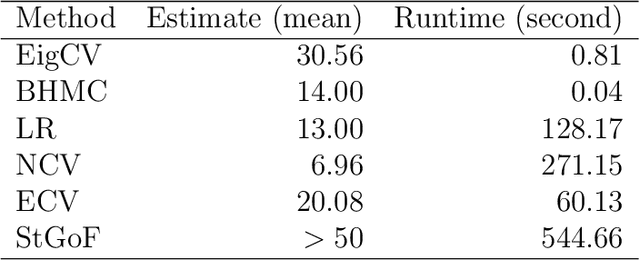
In applied multivariate statistics, estimating the number of latent dimensions or the number of clusters is a fundamental and recurring problem. One common diagnostic is the scree plot, which shows the largest eigenvalues of the data matrix; the user searches for a "gap" or "elbow" in the decreasing eigenvalues; unfortunately, these patterns can hide beneath the bias of the sample eigenvalues. This methodological problem is conceptually difficult because, in many situations, there is only enough signal to detect a subset of the $k$ population dimensions/eigenvectors. In this situation, one could argue that the correct choice of $k$ is the number of detectable dimensions. We alleviate these problems with cross-validated eigenvalues. Under a large class of random graph models, without any parametric assumptions, we provide a p-value for each sample eigenvector. It tests the null hypothesis that this sample eigenvector is orthogonal to (i.e., uncorrelated with) the true latent dimensions. This approach naturally adapts to problems where some dimensions are not statistically detectable. In scenarios where all $k$ dimensions can be estimated, we prove that our procedure consistently estimates $k$. In simulations and a data example, the proposed estimator compares favorably to alternative approaches in both computational and statistical performance.

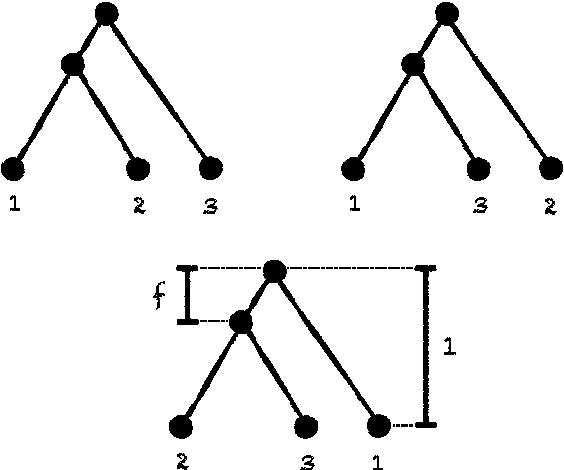
Distance-based species tree estimation: information-theoretic trade-off between number of loci and sequence length under the coalescent

We consider the reconstruction of a phylogeny from multiple genes under the multispecies coalescent. We establish a connection with the sparse signal detection problem, where one seeks to distinguish between a distribution and a mixture of the distribution and a sparse signal. Using this connection, we derive an information-theoretic trade-off between the number of genes, $m$, needed for an accurate reconstruction and the sequence length, $k$, of the genes. Specifically, we show that to detect a branch of length $f$, one needs $m = \Theta(1/[f^{2} \sqrt{k}])$.

Coalescent-based species tree estimation: a stochastic Farris transform

The reconstruction of a species phylogeny from genomic data faces two significant hurdles: 1) the trees describing the evolution of each individual gene--i.e., the gene trees--may differ from the species phylogeny and 2) the molecular sequences corresponding to each gene often provide limited information about the gene trees themselves. In this paper we consider an approach to species tree reconstruction that addresses both these hurdles. Specifically, we propose an algorithm for phylogeny reconstruction under the multispecies coalescent model with a standard model of site substitution. The multispecies coalescent is commonly used to model gene tree discordance due to incomplete lineage sorting, a well-studied population-genetic effect. In previous work, an information-theoretic trade-off was derived in this context between the number of loci, $m$, needed for an accurate reconstruction and the length of the locus sequences, $k$. It was shown that to reconstruct an internal branch of length $f$, one needs $m$ to be of the order of $1/[f^{2} \sqrt{k}]$. That previous result was obtained under the molecular clock assumption, i.e., under the assumption that mutation rates (as well as population sizes) are constant across the species phylogeny. Here we generalize this result beyond the restrictive molecular clock assumption, and obtain a new reconstruction algorithm that has the same data requirement (up to log factors). Our main contribution is a novel reduction to the molecular clock case under the multispecies coalescent. As a corollary, we also obtain a new identifiability result of independent interest: for any species tree with $n \geq 3$ species, the rooted species tree can be identified from the distribution of its unrooted weighted gene trees even in the absence of a molecular clock.

Data Requirement for Phylogenetic Inference from Multiple Loci: A New Distance Method

We consider the problem of estimating the evolutionary history of a set of species (phylogeny or species tree) from several genes. It is known that the evolutionary history of individual genes (gene trees) might be topologically distinct from each other and from the underlying species tree, possibly confounding phylogenetic analysis. A further complication in practice is that one has to estimate gene trees from molecular sequences of finite length. We provide the first full data-requirement analysis of a species tree reconstruction method that takes into account estimation errors at the gene level. Under that criterion, we also devise a novel reconstruction algorithm that provably improves over all previous methods in a regime of interest.

Robust estimation of latent tree graphical models: Inferring hidden states with inexact parameters

Latent tree graphical models are widely used in computational biology, signal and image processing, and network tomography. Here we design a new efficient, estimation procedure for latent tree models, including Gaussian and discrete, reversible models, that significantly improves on previous sample requirement bounds. Our techniques are based on a new hidden state estimator which is robust to inaccuracies in estimated parameters. More precisely, we prove that latent tree models can be estimated with high probability in the so-called Kesten-Stigum regime with $O(log^2 n)$ samples where $n$ is the number of nodes.