Distance-based species tree estimation: information-theoretic trade-off between number of loci and sequence length under the coalescent
Paper and Code
Jul 20, 2017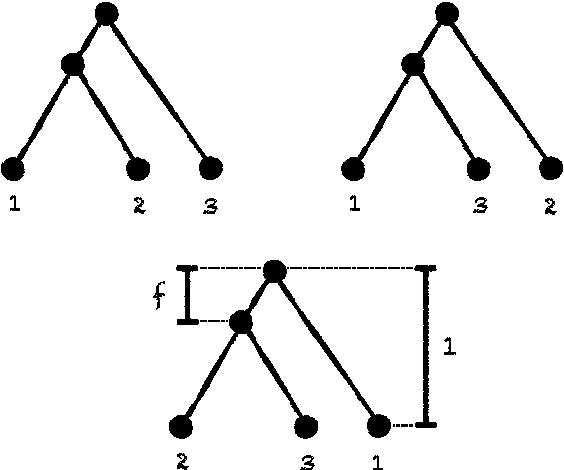
We consider the reconstruction of a phylogeny from multiple genes under the multispecies coalescent. We establish a connection with the sparse signal detection problem, where one seeks to distinguish between a distribution and a mixture of the distribution and a sparse signal. Using this connection, we derive an information-theoretic trade-off between the number of genes, $m$, needed for an accurate reconstruction and the sequence length, $k$, of the genes. Specifically, we show that to detect a branch of length $f$, one needs $m = \Theta(1/[f^{2} \sqrt{k}])$.
* To appear in The Annals of Applied Probability
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge