MiniMax-M1: Scaling Test-Time Compute Efficiently with Lightning Attention

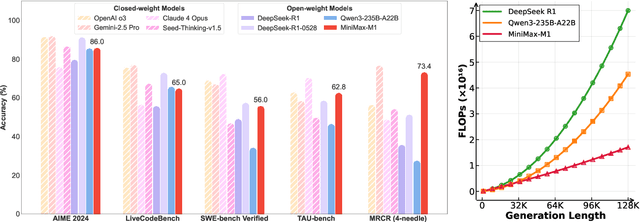
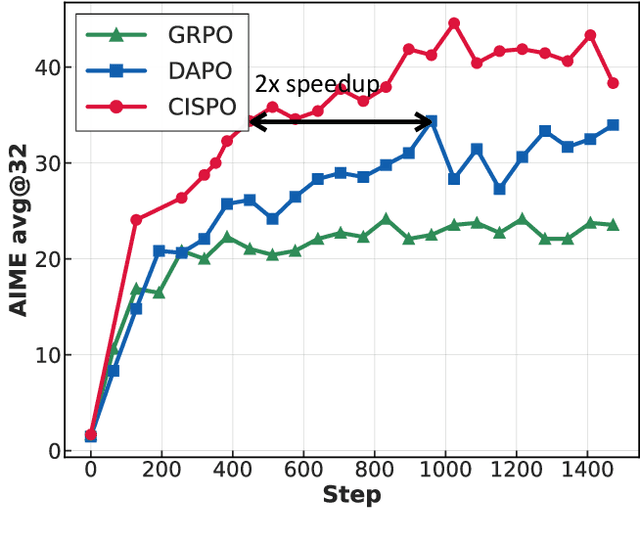
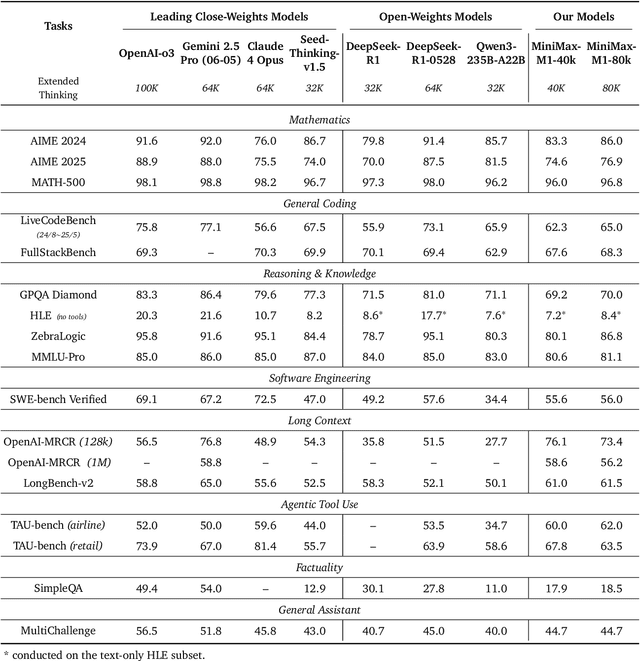
We introduce MiniMax-M1, the world's first open-weight, large-scale hybrid-attention reasoning model. MiniMax-M1 is powered by a hybrid Mixture-of-Experts (MoE) architecture combined with a lightning attention mechanism. The model is developed based on our previous MiniMax-Text-01 model, which contains a total of 456 billion parameters with 45.9 billion parameters activated per token. The M1 model natively supports a context length of 1 million tokens, 8x the context size of DeepSeek R1. Furthermore, the lightning attention mechanism in MiniMax-M1 enables efficient scaling of test-time compute. These properties make M1 particularly suitable for complex tasks that require processing long inputs and thinking extensively. MiniMax-M1 is trained using large-scale reinforcement learning (RL) on diverse problems including sandbox-based, real-world software engineering environments. In addition to M1's inherent efficiency advantage for RL training, we propose CISPO, a novel RL algorithm to further enhance RL efficiency. CISPO clips importance sampling weights rather than token updates, outperforming other competitive RL variants. Combining hybrid-attention and CISPO enables MiniMax-M1's full RL training on 512 H800 GPUs to complete in only three weeks, with a rental cost of just $534,700. We release two versions of MiniMax-M1 models with 40K and 80K thinking budgets respectively, where the 40K model represents an intermediate phase of the 80K training. Experiments on standard benchmarks show that our models are comparable or superior to strong open-weight models such as the original DeepSeek-R1 and Qwen3-235B, with particular strengths in complex software engineering, tool utilization, and long-context tasks. We publicly release MiniMax-M1 at https://github.com/MiniMax-AI/MiniMax-M1.

MiniMax-01: Scaling Foundation Models with Lightning Attention

We introduce MiniMax-01 series, including MiniMax-Text-01 and MiniMax-VL-01, which are comparable to top-tier models while offering superior capabilities in processing longer contexts. The core lies in lightning attention and its efficient scaling. To maximize computational capacity, we integrate it with Mixture of Experts (MoE), creating a model with 32 experts and 456 billion total parameters, of which 45.9 billion are activated for each token. We develop an optimized parallel strategy and highly efficient computation-communication overlap techniques for MoE and lightning attention. This approach enables us to conduct efficient training and inference on models with hundreds of billions of parameters across contexts spanning millions of tokens. The context window of MiniMax-Text-01 can reach up to 1 million tokens during training and extrapolate to 4 million tokens during inference at an affordable cost. Our vision-language model, MiniMax-VL-01 is built through continued training with 512 billion vision-language tokens. Experiments on both standard and in-house benchmarks show that our models match the performance of state-of-the-art models like GPT-4o and Claude-3.5-Sonnet while offering 20-32 times longer context window. We publicly release MiniMax-01 at https://github.com/MiniMax-AI.

Estimating Graph Dimension with Cross-validated Eigenvalues

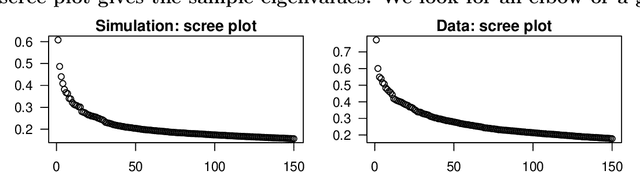
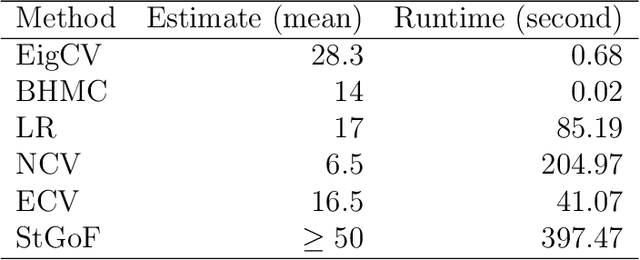
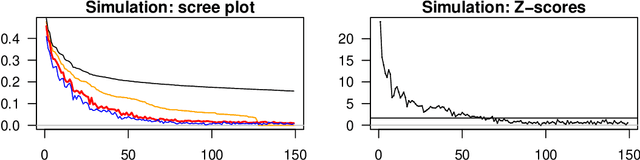
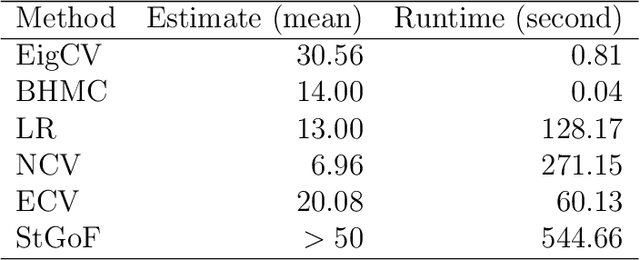
In applied multivariate statistics, estimating the number of latent dimensions or the number of clusters is a fundamental and recurring problem. One common diagnostic is the scree plot, which shows the largest eigenvalues of the data matrix; the user searches for a "gap" or "elbow" in the decreasing eigenvalues; unfortunately, these patterns can hide beneath the bias of the sample eigenvalues. This methodological problem is conceptually difficult because, in many situations, there is only enough signal to detect a subset of the $k$ population dimensions/eigenvectors. In this situation, one could argue that the correct choice of $k$ is the number of detectable dimensions. We alleviate these problems with cross-validated eigenvalues. Under a large class of random graph models, without any parametric assumptions, we provide a p-value for each sample eigenvector. It tests the null hypothesis that this sample eigenvector is orthogonal to (i.e., uncorrelated with) the true latent dimensions. This approach naturally adapts to problems where some dimensions are not statistically detectable. In scenarios where all $k$ dimensions can be estimated, we prove that our procedure consistently estimates $k$. In simulations and a data example, the proposed estimator compares favorably to alternative approaches in both computational and statistical performance.