Satyanath Bhat
Topic Model Based Multi-Label Classification from the Crowd
Apr 04, 2016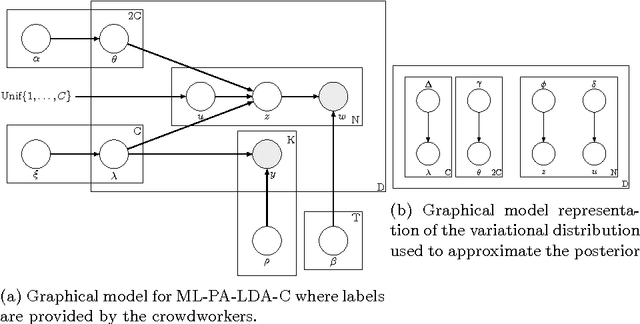

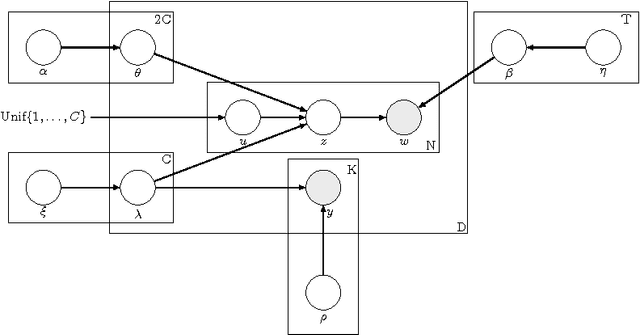
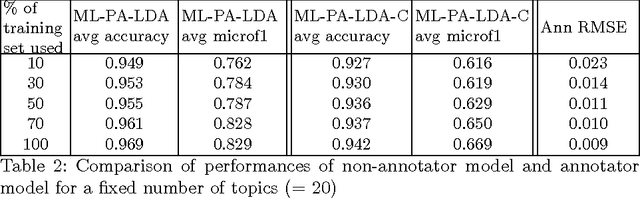
Abstract:Multi-label classification is a common supervised machine learning problem where each instance is associated with multiple classes. The key challenge in this problem is learning the correlations between the classes. An additional challenge arises when the labels of the training instances are provided by noisy, heterogeneous crowdworkers with unknown qualities. We first assume labels from a perfect source and propose a novel topic model where the present as well as the absent classes generate the latent topics and hence the words. We non-trivially extend our topic model to the scenario where the labels are provided by noisy crowdworkers. Extensive experimentation on real world datasets reveals the superior performance of the proposed model. The proposed model learns the qualities of the annotators as well, even with minimal training data.
A Truthful Mechanism with Biparameter Learning for Online Crowdsourcing
Feb 12, 2016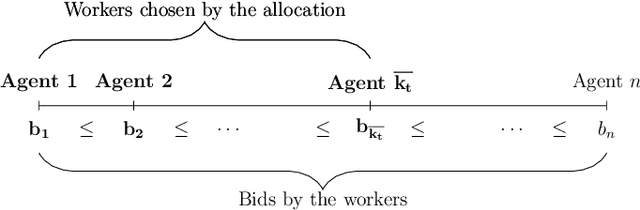
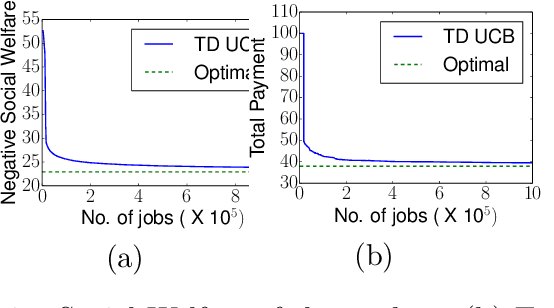
Abstract:We study a problem of allocating divisible jobs, arriving online, to workers in a crowdsourcing setting which involves learning two parameters of strategically behaving workers. Each job is split into a certain number of tasks that are then allocated to workers. Each arriving job has to be completed within a deadline and each task has to be completed satisfying an upper bound on probability of failure. The job population is homogeneous while the workers are heterogeneous in terms of costs, completion times, and times to failure. The job completion time and time to failure of each worker are stochastic with fixed but unknown means. The requester is faced with the challenge of learning two separate parameters of each (strategically behaving) worker simultaneously, namely, the mean job completion time and the mean time to failure. The time to failure of a worker depends on the duration of the task handled by the worker. Assuming non-strategic workers to start with, we solve this biparameter learning problem by applying the Robust UCB algorithm. Then, we non-trivially extend this algorithm to the setting where the workers are strategic about their costs. Our proposed mechanism is dominant strategy incentive compatible and ex-post individually rational with asymptotically optimal regret performance.
A Robust UCB Scheme for Active Learning in Regression from Strategic Crowds
Jan 29, 2016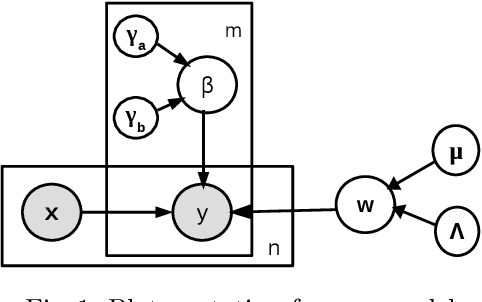
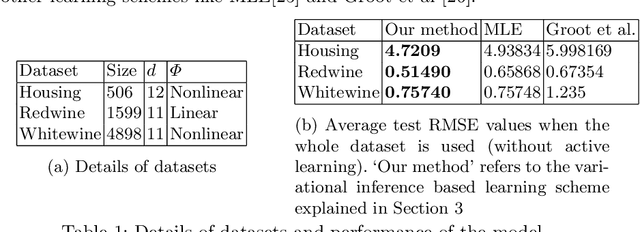

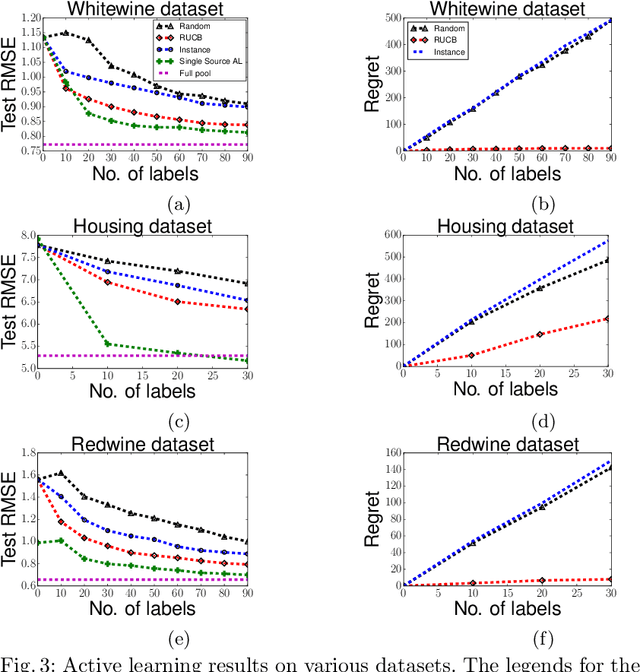
Abstract:We study the problem of training an accurate linear regression model by procuring labels from multiple noisy crowd annotators, under a budget constraint. We propose a Bayesian model for linear regression in crowdsourcing and use variational inference for parameter estimation. To minimize the number of labels crowdsourced from the annotators, we adopt an active learning approach. In this specific context, we prove the equivalence of well-studied criteria of active learning like entropy minimization and expected error reduction. Interestingly, we observe that we can decouple the problems of identifying an optimal unlabeled instance and identifying an annotator to label it. We observe a useful connection between the multi-armed bandit framework and the annotator selection in active learning. Due to the nature of the distribution of the rewards on the arms, we use the Robust Upper Confidence Bound (UCB) scheme with truncated empirical mean estimator to solve the annotator selection problem. This yields provable guarantees on the regret. We further apply our model to the scenario where annotators are strategic and design suitable incentives to induce them to put in their best efforts.
An Incentive Compatible Multi-Armed-Bandit Crowdsourcing Mechanism with Quality Assurance
Jun 17, 2015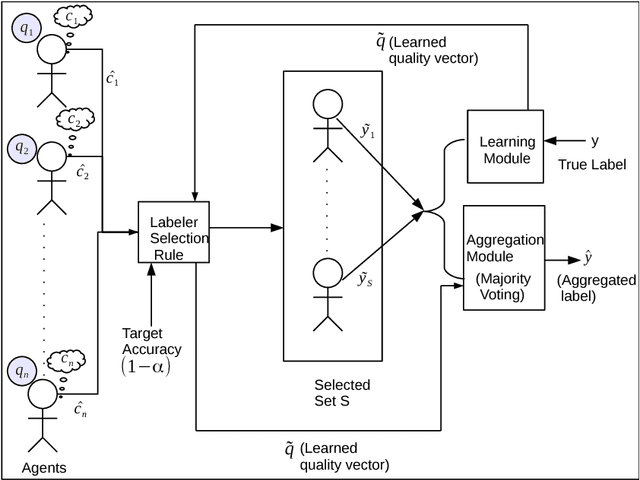

Abstract:Consider a requester who wishes to crowdsource a series of identical binary labeling tasks to a pool of workers so as to achieve an assured accuracy for each task, in a cost optimal way. The workers are heterogeneous with unknown but fixed qualities and their costs are private. The problem is to select for each task an optimal subset of workers so that the outcome obtained from the selected workers guarantees a target accuracy level. The problem is a challenging one even in a non strategic setting since the accuracy of aggregated label depends on unknown qualities. We develop a novel multi-armed bandit (MAB) mechanism for solving this problem. First, we propose a framework, Assured Accuracy Bandit (AAB), which leads to an MAB algorithm, Constrained Confidence Bound for a Non Strategic setting (CCB-NS). We derive an upper bound on the number of time steps the algorithm chooses a sub-optimal set that depends on the target accuracy level and true qualities. A more challenging situation arises when the requester not only has to learn the qualities of the workers but also elicit their true costs. We modify the CCB-NS algorithm to obtain an adaptive exploration separated algorithm which we call { \em Constrained Confidence Bound for a Strategic setting (CCB-S)}. CCB-S algorithm produces an ex-post monotone allocation rule and thus can be transformed into an ex-post incentive compatible and ex-post individually rational mechanism that learns the qualities of the workers and guarantees a given target accuracy level in a cost optimal way. We provide a lower bound on the number of times any algorithm should select a sub-optimal set and we see that the lower bound matches our upper bound upto a constant factor. We provide insights on the practical implementation of this framework through an illustrative example and we show the efficacy of our algorithms through simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge