An Incentive Compatible Multi-Armed-Bandit Crowdsourcing Mechanism with Quality Assurance
Paper and Code
Jun 17, 2015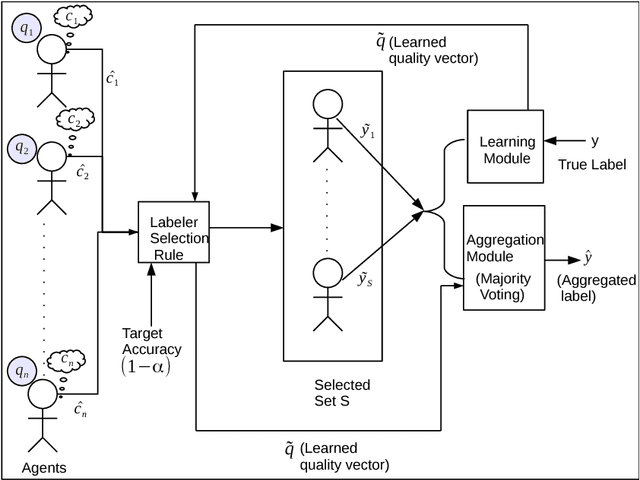

Consider a requester who wishes to crowdsource a series of identical binary labeling tasks to a pool of workers so as to achieve an assured accuracy for each task, in a cost optimal way. The workers are heterogeneous with unknown but fixed qualities and their costs are private. The problem is to select for each task an optimal subset of workers so that the outcome obtained from the selected workers guarantees a target accuracy level. The problem is a challenging one even in a non strategic setting since the accuracy of aggregated label depends on unknown qualities. We develop a novel multi-armed bandit (MAB) mechanism for solving this problem. First, we propose a framework, Assured Accuracy Bandit (AAB), which leads to an MAB algorithm, Constrained Confidence Bound for a Non Strategic setting (CCB-NS). We derive an upper bound on the number of time steps the algorithm chooses a sub-optimal set that depends on the target accuracy level and true qualities. A more challenging situation arises when the requester not only has to learn the qualities of the workers but also elicit their true costs. We modify the CCB-NS algorithm to obtain an adaptive exploration separated algorithm which we call { \em Constrained Confidence Bound for a Strategic setting (CCB-S)}. CCB-S algorithm produces an ex-post monotone allocation rule and thus can be transformed into an ex-post incentive compatible and ex-post individually rational mechanism that learns the qualities of the workers and guarantees a given target accuracy level in a cost optimal way. We provide a lower bound on the number of times any algorithm should select a sub-optimal set and we see that the lower bound matches our upper bound upto a constant factor. We provide insights on the practical implementation of this framework through an illustrative example and we show the efficacy of our algorithms through simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge