AdaBoost and robust one-bit compressed sensing

This paper studies binary classification in robust one-bit compressed sensing with adversarial errors. It is assumed that the model is overparameterized and that the parameter of interest is effectively sparse. AdaBoost is considered, and, through its relation to the max-$\ell_1$-margin-classifier, risk bounds are derived. In particular, this provides an explanation why interpolating adversarial noise can be harmless for classification problems. Simulations illustrate the presented theory.

Minimum $\ell_1-$norm interpolation via basis pursuit is robust to errors

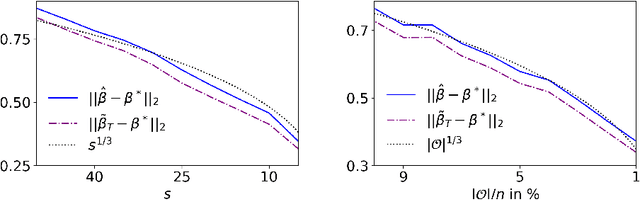
This article studies basis pursuit, i.e. minimum $\ell_1$-norm interpolation, in sparse linear regression with additive errors. No conditions on the errors are imposed. It is assumed that the number of i.i.d. Gaussian features grows superlinear in the number of samples. The main result is that under these conditions the Euclidean error of recovering the true regressor is of the order of the average noise level. Hence, the regressor recovered by basis pursuit is close to the truth if the average noise level is small. Lower bounds that show near optimality of the results complement the analysis. In addition, these results are extended to low rank trace regression. The proofs rely on new lower tail bounds for maxima of Gaussians vectors and the spectral norm of Gaussian matrices, respectively, and might be of independent interest as they are significantly stronger than the corresponding upper tail bounds.

Oracle inequalities for image denoising with total variation regularization

We derive oracle results for discrete image denoising with a total variation penalty. We consider the least squares estimator with a penalty on the $\ell^1$-norm of the total discrete derivative of the image. This estimator falls into the class of analysis estimators. A bound on the effective sparsity by means of an interpolating matrix allows us to obtain oracle inequalities with fast rates. The bound is an extension of the bound by Ortelli and van de Geer [2019c] to the two-dimensional case. We also present an oracle inequality with slow rates, which matches, up to a log-term, the rate obtained for the same estimator by Mammen and van de Geer [1997]. The key ingredient for our results are the projection arguments to bound the empirical process due to Dalalyan et al. [2017].

A Framework for the construction of upper bounds on the number of affine linear regions of ReLU feed-forward neural networks

In this work we present a new framework to derive upper bounds on the number regions of feed-forward neural nets with ReLU activation functions. We derive all existing such bounds as special cases, however in a different representation in terms of matrices. This provides new insight and allows a more detailed analysis of the corresponding bounds. In particular, we provide a Jordan-like decomposition for the involved matrices and present new tighter results for an asymptotic setting. Moreover, new even stronger bounds may be obtained from our framework.

Asymptotic Confidence Regions for High-dimensional Structured Sparsity

In the setting of high-dimensional linear regression models, we propose two frameworks for constructing pointwise and group confidence sets for penalized estimators which incorporate prior knowledge about the organization of the non-zero coefficients. This is done by desparsifying the estimator as in van de Geer et al. [18] and van de Geer and Stucky [17], then using an appropriate estimator for the precision matrix $\Theta$. In order to estimate the precision matrix a corresponding structured matrix norm penalty has to be introduced. After normalization the result is an asymptotic pivot. The asymptotic behavior is studied and simulations are added to study the differences between the two schemes.

High-dimensional additive modeling

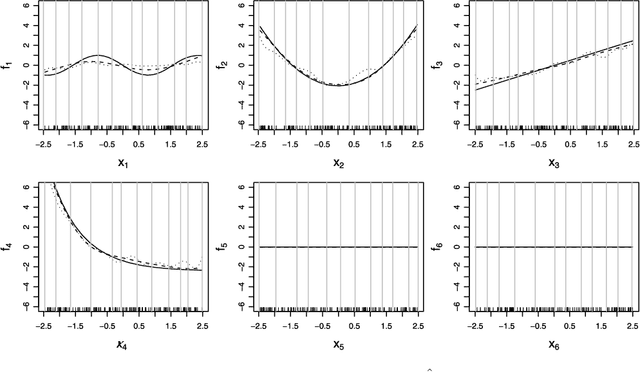
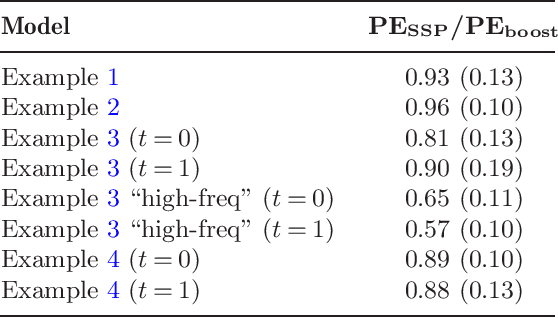
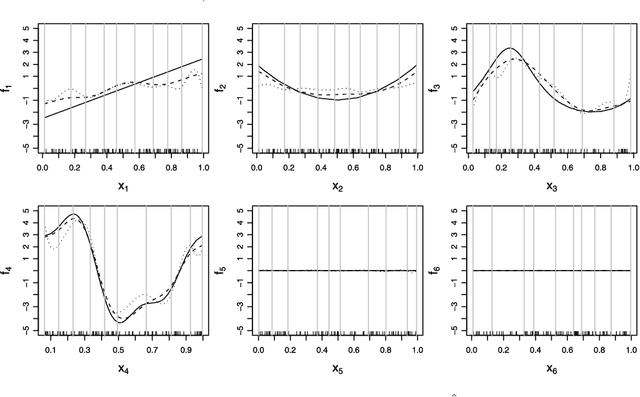
We propose a new sparsity-smoothness penalty for high-dimensional generalized additive models. The combination of sparsity and smoothness is crucial for mathematical theory as well as performance for finite-sample data. We present a computationally efficient algorithm, with provable numerical convergence properties, for optimizing the penalized likelihood. Furthermore, we provide oracle results which yield asymptotic optimality of our estimator for high dimensional but sparse additive models. Finally, an adaptive version of our sparsity-smoothness penalized approach yields large additional performance gains.

Adaptive Lasso for High Dimensional Regression and Gaussian Graphical Modeling

We show that the two-stage adaptive Lasso procedure (Zou, 2006) is consistent for high-dimensional model selection in linear and Gaussian graphical models. Our conditions for consistency cover more general situations than those accomplished in previous work: we prove that restricted eigenvalue conditions (Bickel et al., 2008) are also sufficient for sparse structure estimation.

Taking Advantage of Sparsity in Multi-Task Learning

We study the problem of estimating multiple linear regression equations for the purpose of both prediction and variable selection. Following recent work on multi-task learning Argyriou et al. [2008], we assume that the regression vectors share the same sparsity pattern. This means that the set of relevant predictor variables is the same across the different equations. This assumption leads us to consider the Group Lasso as a candidate estimation method. We show that this estimator enjoys nice sparsity oracle inequalities and variable selection properties. The results hold under a certain restricted eigenvalue condition and a coherence condition on the design matrix, which naturally extend recent work in Bickel et al. [2007], Lounici [2008]. In particular, in the multi-task learning scenario, in which the number of tasks can grow, we are able to remove completely the effect of the number of predictor variables in the bounds. Finally, we show how our results can be extended to more general noise distributions, of which we only require the variance to be finite.