AdaBoost and robust one-bit compressed sensing

This paper studies binary classification in robust one-bit compressed sensing with adversarial errors. It is assumed that the model is overparameterized and that the parameter of interest is effectively sparse. AdaBoost is considered, and, through its relation to the max-$\ell_1$-margin-classifier, risk bounds are derived. In particular, this provides an explanation why interpolating adversarial noise can be harmless for classification problems. Simulations illustrate the presented theory.

Minimum $\ell_1-$norm interpolation via basis pursuit is robust to errors

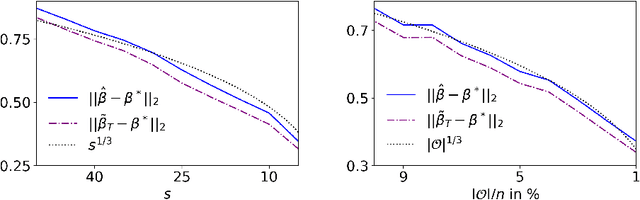
This article studies basis pursuit, i.e. minimum $\ell_1$-norm interpolation, in sparse linear regression with additive errors. No conditions on the errors are imposed. It is assumed that the number of i.i.d. Gaussian features grows superlinear in the number of samples. The main result is that under these conditions the Euclidean error of recovering the true regressor is of the order of the average noise level. Hence, the regressor recovered by basis pursuit is close to the truth if the average noise level is small. Lower bounds that show near optimality of the results complement the analysis. In addition, these results are extended to low rank trace regression. The proofs rely on new lower tail bounds for maxima of Gaussians vectors and the spectral norm of Gaussian matrices, respectively, and might be of independent interest as they are significantly stronger than the corresponding upper tail bounds.

Computationally efficient sparse clustering

We study statistical and computational limits of clustering when the means of the centres are sparse and their dimension is possibly much larger than the sample size. Our theoretical analysis focuses on the simple model $X_i = z_i \theta + \varepsilon_i$, $z_i \in \{-1,1\}$, $\varepsilon_i \thicksim \mathcal{N}(0, I)$, which has two clusters with centres $\theta$ and $-\theta$. We provide a finite sample analysis of a new sparse clustering algorithm based on sparse PCA and show that it achieves the minimax optimal misclustering rate in the regime $\|\theta\| \rightarrow \infty$, matching asymptotically the Bayes error. Our results require the sparsity to grow slower than the square root of the sample size. Using a recent framework for computational lower bounds---the low-degree likelihood ratio---we give evidence that this condition is necessary for any polynomial-time clustering algorithm to succeed below the BBP threshold. This complements existing evidence based on reductions and statistical query lower bounds. Compared to these existing results, we cover a wider set of parameter regimes and give a more precise understanding of the runtime required and the misclustering error achievable. We also discuss extensions of our results to more than two clusters.

Optimality of Spectral Clustering for Gaussian Mixture Model

Spectral clustering is one of the most popular algorithms to group high dimensional data. It is easy to implement and computationally efficient. Despite its popularity and successful applications, its theoretical properties have not been fully understood. The spectral clustering algorithm is often used as a consistent initializer for more sophisticated clustering algorithms. However, in this paper, we show that spectral clustering is actually already optimal in the Gaussian Mixture Model, when the number of clusters of is fixed and consistent clustering is possible. Contrary to that spectral gap conditions are widely assumed in literature to analyze spectral clustering, these conditions are not needed in this paper to establish its optimality.