AdaBoost and robust one-bit compressed sensing

This paper studies binary classification in robust one-bit compressed sensing with adversarial errors. It is assumed that the model is overparameterized and that the parameter of interest is effectively sparse. AdaBoost is considered, and, through its relation to the max-$\ell_1$-margin-classifier, risk bounds are derived. In particular, this provides an explanation why interpolating adversarial noise can be harmless for classification problems. Simulations illustrate the presented theory.

Minimum $\ell_1-$norm interpolation via basis pursuit is robust to errors

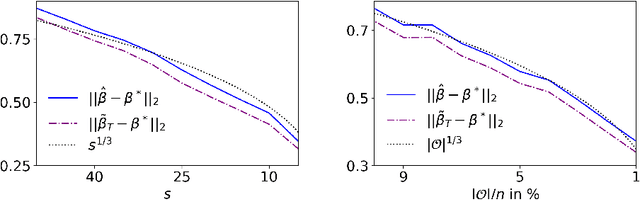
This article studies basis pursuit, i.e. minimum $\ell_1$-norm interpolation, in sparse linear regression with additive errors. No conditions on the errors are imposed. It is assumed that the number of i.i.d. Gaussian features grows superlinear in the number of samples. The main result is that under these conditions the Euclidean error of recovering the true regressor is of the order of the average noise level. Hence, the regressor recovered by basis pursuit is close to the truth if the average noise level is small. Lower bounds that show near optimality of the results complement the analysis. In addition, these results are extended to low rank trace regression. The proofs rely on new lower tail bounds for maxima of Gaussians vectors and the spectral norm of Gaussian matrices, respectively, and might be of independent interest as they are significantly stronger than the corresponding upper tail bounds.

Benign overfitting in the large deviation regime

We investigate the benign overfitting phenomenon in the large deviation regime where the bounds on the prediction risk hold with probability $1-e^{-\zeta n}$, for some absolute constant $\zeta$. We prove that these bounds can converge to $0$ for the quadratic loss. We obtain this result by a new analysis of the interpolating estimator with minimal Euclidean norm, relying on a preliminary localization of this estimator with respect to the Euclidean norm. This new analysis complements and strengthens particular cases obtained in previous works for the square loss and is extended to other loss functions. To illustrate this, we also provide excess risk bounds for the Huber and absolute losses, two widely spread losses in robust statistics.