Better Mixing via Deep Representations

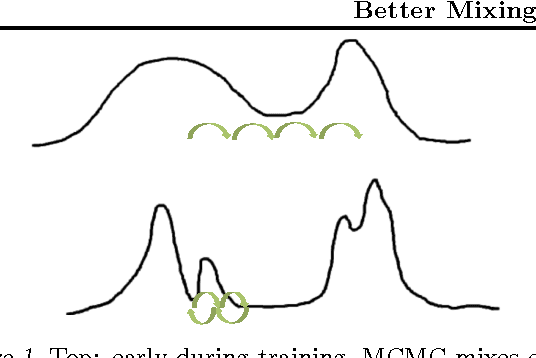
It has previously been hypothesized, and supported with some experimental evidence, that deeper representations, when well trained, tend to do a better job at disentangling the underlying factors of variation. We study the following related conjecture: better representations, in the sense of better disentangling, can be exploited to produce faster-mixing Markov chains. Consequently, mixing would be more efficient at higher levels of representation. To better understand why and how this is happening, we propose a secondary conjecture: the higher-level samples fill more uniformly the space they occupy and the high-density manifolds tend to unfold when represented at higher levels. The paper discusses these hypotheses and tests them experimentally through visualization and measurements of mixing and interpolating between samples.

Implicit Density Estimation by Local Moment Matching to Sample from Auto-Encoders

Recent work suggests that some auto-encoder variants do a good job of capturing the local manifold structure of the unknown data generating density. This paper contributes to the mathematical understanding of this phenomenon and helps define better justified sampling algorithms for deep learning based on auto-encoder variants. We consider an MCMC where each step samples from a Gaussian whose mean and covariance matrix depend on the previous state, defines through its asymptotic distribution a target density. First, we show that good choices (in the sense of consistency) for these mean and covariance functions are the local expected value and local covariance under that target density. Then we show that an auto-encoder with a contractive penalty captures estimators of these local moments in its reconstruction function and its Jacobian. A contribution of this work is thus a novel alternative to maximum-likelihood density estimation, which we call local moment matching. It also justifies a recently proposed sampling algorithm for the Contractive Auto-Encoder and extends it to the Denoising Auto-Encoder.

A Generative Process for Sampling Contractive Auto-Encoders

The contractive auto-encoder learns a representation of the input data that captures the local manifold structure around each data point, through the leading singular vectors of the Jacobian of the transformation from input to representation. The corresponding singular values specify how much local variation is plausible in directions associated with the corresponding singular vectors, while remaining in a high-density region of the input space. This paper proposes a procedure for generating samples that are consistent with the local structure captured by a contractive auto-encoder. The associated stochastic process defines a distribution from which one can sample, and which experimentally appears to converge quickly and mix well between modes, compared to Restricted Boltzmann Machines and Deep Belief Networks. The intuitions behind this procedure can also be used to train the second layer of contraction that pools lower-level features and learns to be invariant to the local directions of variation discovered in the first layer. We show that this can help learn and represent invariances present in the data and improve classification error.

Learning invariant features through local space contraction

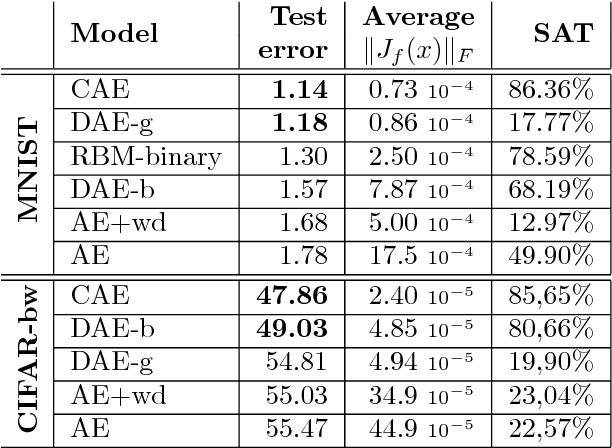
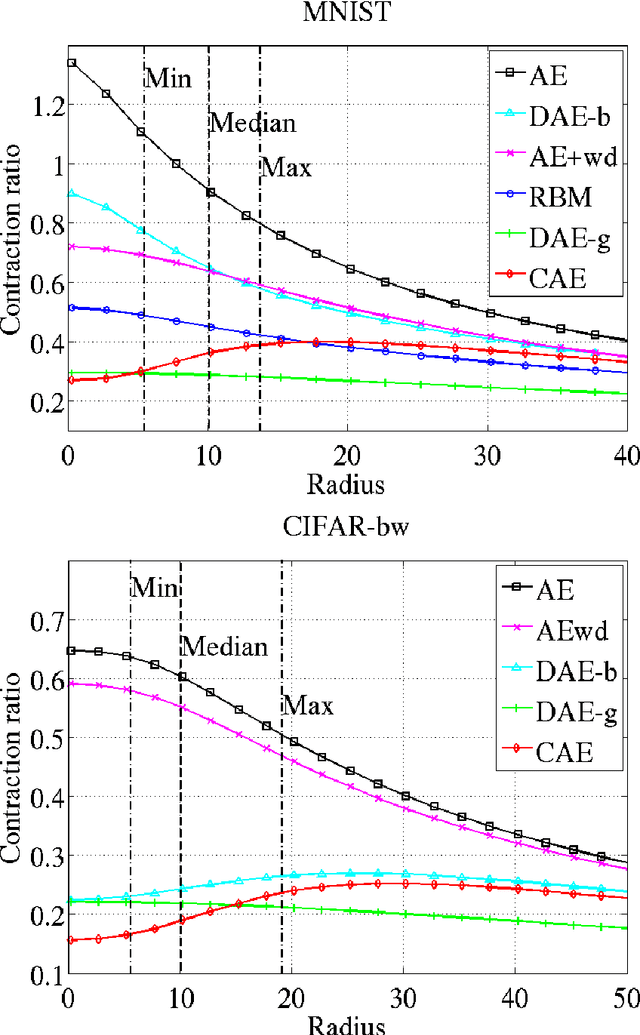
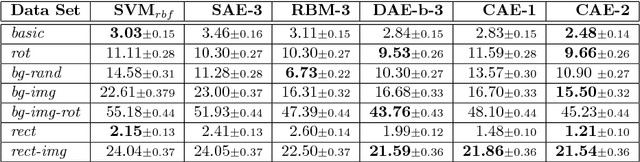
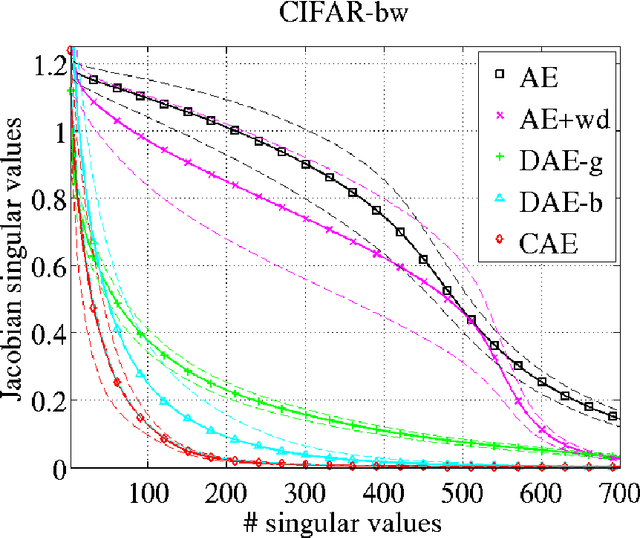
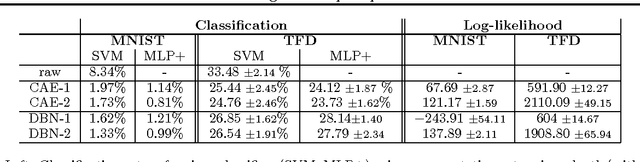
We present in this paper a novel approach for training deterministic auto-encoders. We show that by adding a well chosen penalty term to the classical reconstruction cost function, we can achieve results that equal or surpass those attained by other regularized auto-encoders as well as denoising auto-encoders on a range of datasets. This penalty term corresponds to the Frobenius norm of the Jacobian matrix of the encoder activations with respect to the input. We show that this penalty term results in a localized space contraction which in turn yields robust features on the activation layer. Furthermore, we show how this penalty term is related to both regularized auto-encoders and denoising encoders and how it can be seen as a link between deterministic and non-deterministic auto-encoders. We find empirically that this penalty helps to carve a representation that better captures the local directions of variation dictated by the data, corresponding to a lower-dimensional non-linear manifold, while being more invariant to the vast majority of directions orthogonal to the manifold. Finally, we show that by using the learned features to initialize a MLP, we achieve state of the art classification error on a range of datasets, surpassing other methods of pre-training.

Adding noise to the input of a model trained with a regularized objective

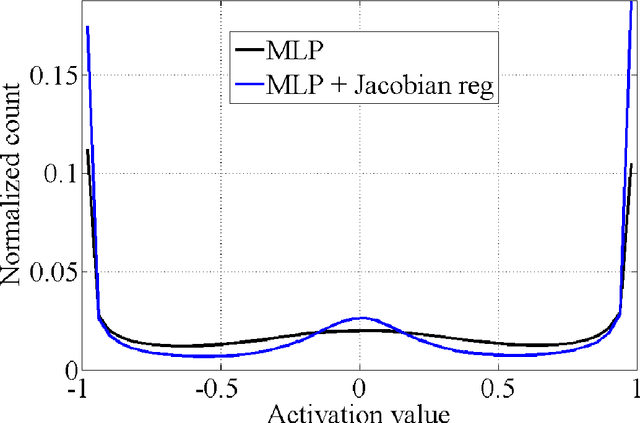
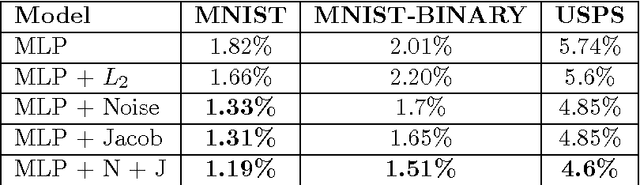
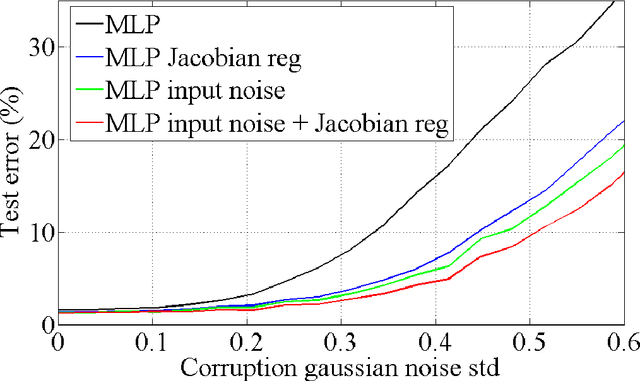
Regularization is a well studied problem in the context of neural networks. It is usually used to improve the generalization performance when the number of input samples is relatively small or heavily contaminated with noise. The regularization of a parametric model can be achieved in different manners some of which are early stopping (Morgan and Bourlard, 1990), weight decay, output smoothing that are used to avoid overfitting during the training of the considered model. From a Bayesian point of view, many regularization techniques correspond to imposing certain prior distributions on model parameters (Krogh and Hertz, 1991). Using Bishop's approximation (Bishop, 1995) of the objective function when a restricted type of noise is added to the input of a parametric function, we derive the higher order terms of the Taylor expansion and analyze the coefficients of the regularization terms induced by the noisy input. In particular we study the effect of penalizing the Hessian of the mapping function with respect to the input in terms of generalization performance. We also show how we can control independently this coefficient by explicitly penalizing the Jacobian of the mapping function on corrupted inputs.

Deep Self-Taught Learning for Handwritten Character Recognition

Recent theoretical and empirical work in statistical machine learning has demonstrated the importance of learning algorithms for deep architectures, i.e., function classes obtained by composing multiple non-linear transformations. Self-taught learning (exploiting unlabeled examples or examples from other distributions) has already been applied to deep learners, but mostly to show the advantage of unlabeled examples. Here we explore the advantage brought by {\em out-of-distribution examples}. For this purpose we developed a powerful generator of stochastic variations and noise processes for character images, including not only affine transformations but also slant, local elastic deformations, changes in thickness, background images, grey level changes, contrast, occlusion, and various types of noise. The out-of-distribution examples are obtained from these highly distorted images or by including examples of object classes different from those in the target test set. We show that {\em deep learners benefit more from out-of-distribution examples than a corresponding shallow learner}, at least in the area of handwritten character recognition. In fact, we show that they beat previously published results and reach human-level performance on both handwritten digit classification and 62-class handwritten character recognition.