Better Mixing via Deep Representations
Paper and Code
Jul 18, 2012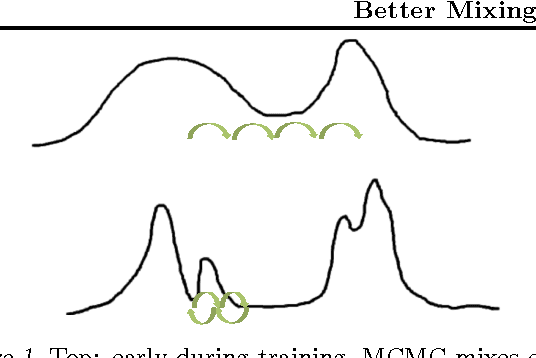
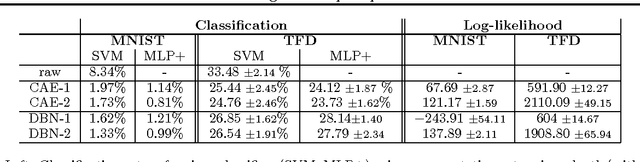


It has previously been hypothesized, and supported with some experimental evidence, that deeper representations, when well trained, tend to do a better job at disentangling the underlying factors of variation. We study the following related conjecture: better representations, in the sense of better disentangling, can be exploited to produce faster-mixing Markov chains. Consequently, mixing would be more efficient at higher levels of representation. To better understand why and how this is happening, we propose a secondary conjecture: the higher-level samples fill more uniformly the space they occupy and the high-density manifolds tend to unfold when represented at higher levels. The paper discusses these hypotheses and tests them experimentally through visualization and measurements of mixing and interpolating between samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge