Learning invariant features through local space contraction
Paper and Code
Apr 21, 2011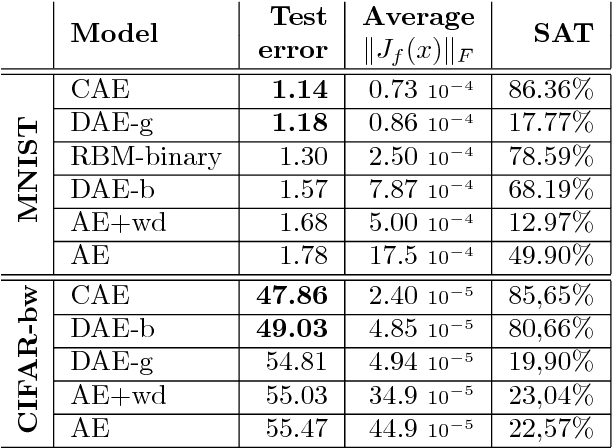
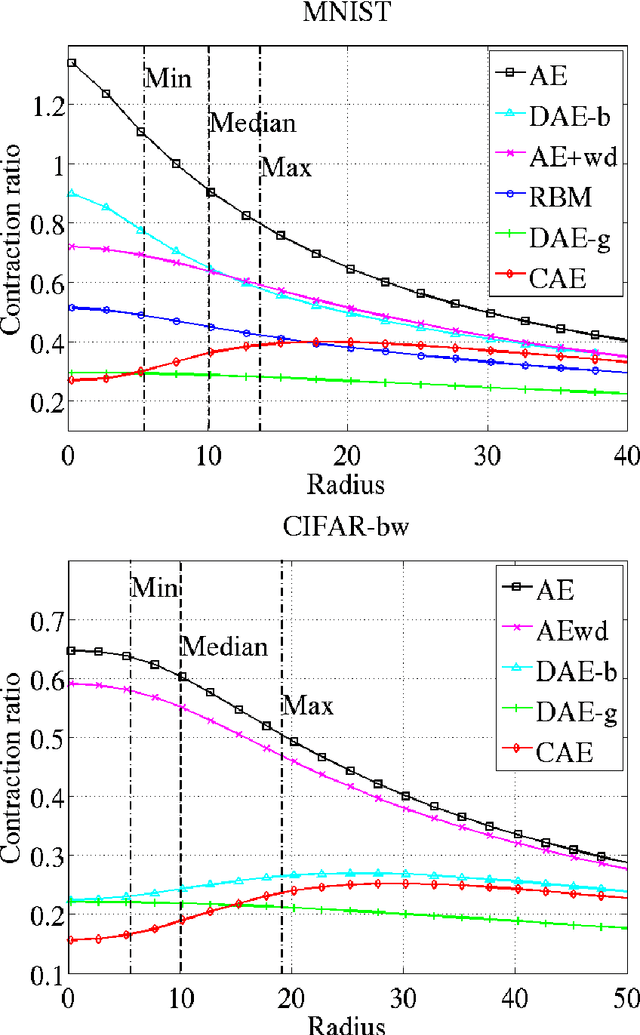
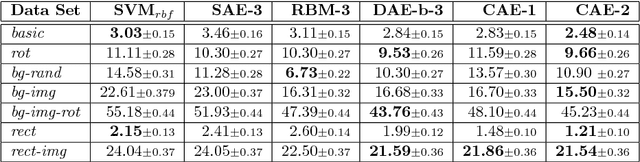
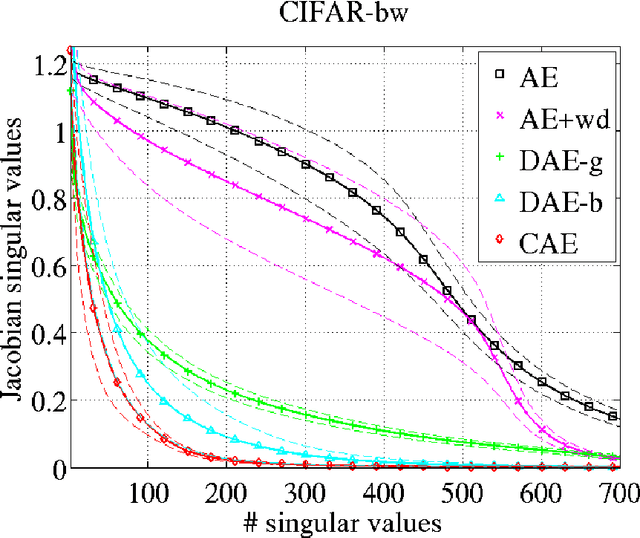
We present in this paper a novel approach for training deterministic auto-encoders. We show that by adding a well chosen penalty term to the classical reconstruction cost function, we can achieve results that equal or surpass those attained by other regularized auto-encoders as well as denoising auto-encoders on a range of datasets. This penalty term corresponds to the Frobenius norm of the Jacobian matrix of the encoder activations with respect to the input. We show that this penalty term results in a localized space contraction which in turn yields robust features on the activation layer. Furthermore, we show how this penalty term is related to both regularized auto-encoders and denoising encoders and how it can be seen as a link between deterministic and non-deterministic auto-encoders. We find empirically that this penalty helps to carve a representation that better captures the local directions of variation dictated by the data, corresponding to a lower-dimensional non-linear manifold, while being more invariant to the vast majority of directions orthogonal to the manifold. Finally, we show that by using the learned features to initialize a MLP, we achieve state of the art classification error on a range of datasets, surpassing other methods of pre-training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge