Saket Tiwari
Spectral Collapse Drives Loss of Plasticity in Deep Continual Learning
Sep 26, 2025Abstract:We investigate why deep neural networks suffer from \emph{loss of plasticity} in deep continual learning, failing to learn new tasks without reinitializing parameters. We show that this failure is preceded by Hessian spectral collapse at new-task initialization, where meaningful curvature directions vanish and gradient descent becomes ineffective. To characterize the necessary condition for successful training, we introduce the notion of $\tau$-trainability and show that current plasticity preserving algorithms can be unified under this framework. Targeting spectral collapse directly, we then discuss the Kronecker factored approximation of the Hessian, which motivates two regularization enhancements: maintaining high effective feature rank and applying $L2$ penalties. Experiments on continual supervised and reinforcement learning tasks confirm that combining these two regularizers effectively preserves plasticity.
Geometry of Neural Reinforcement Learning in Continuous State and Action Spaces
Jul 28, 2025Abstract:Advances in reinforcement learning (RL) have led to its successful application in complex tasks with continuous state and action spaces. Despite these advances in practice, most theoretical work pertains to finite state and action spaces. We propose building a theoretical understanding of continuous state and action spaces by employing a geometric lens to understand the locally attained set of states. The set of all parametrised policies learnt through a semi-gradient based approach induces a set of attainable states in RL. We show that the training dynamics of a two-layer neural policy induce a low dimensional manifold of attainable states embedded in the high-dimensional nominal state space trained using an actor-critic algorithm. We prove that, under certain conditions, the dimensionality of this manifold is of the order of the dimensionality of the action space. This is the first result of its kind, linking the geometry of the state space to the dimensionality of the action space. We empirically corroborate this upper bound for four MuJoCo environments and also demonstrate the results in a toy environment with varying dimensionality. We also show the applicability of this theoretical result by introducing a local manifold learning layer to the policy and value function networks to improve the performance in control environments with very high degrees of freedom by changing one layer of the neural network to learn sparse representations.
A Domain-Agnostic Approach for Characterization of Lifelong Learning Systems
Jan 18, 2023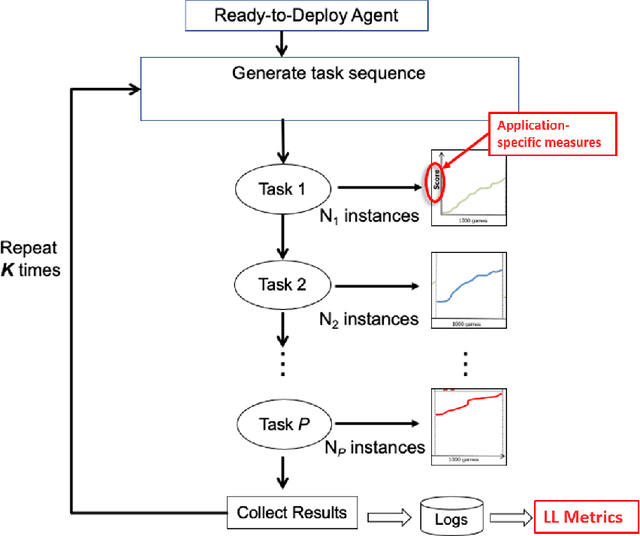
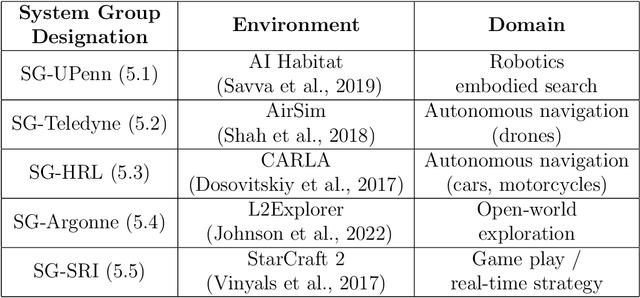


Abstract:Despite the advancement of machine learning techniques in recent years, state-of-the-art systems lack robustness to "real world" events, where the input distributions and tasks encountered by the deployed systems will not be limited to the original training context, and systems will instead need to adapt to novel distributions and tasks while deployed. This critical gap may be addressed through the development of "Lifelong Learning" systems that are capable of 1) Continuous Learning, 2) Transfer and Adaptation, and 3) Scalability. Unfortunately, efforts to improve these capabilities are typically treated as distinct areas of research that are assessed independently, without regard to the impact of each separate capability on other aspects of the system. We instead propose a holistic approach, using a suite of metrics and an evaluation framework to assess Lifelong Learning in a principled way that is agnostic to specific domains or system techniques. Through five case studies, we show that this suite of metrics can inform the development of varied and complex Lifelong Learning systems. We highlight how the proposed suite of metrics quantifies performance trade-offs present during Lifelong Learning system development - both the widely discussed Stability-Plasticity dilemma and the newly proposed relationship between Sample Efficient and Robust Learning. Further, we make recommendations for the formulation and use of metrics to guide the continuing development of Lifelong Learning systems and assess their progress in the future.
Effects of Data Geometry in Early Deep Learning
Dec 29, 2022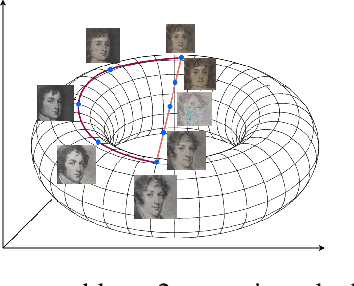
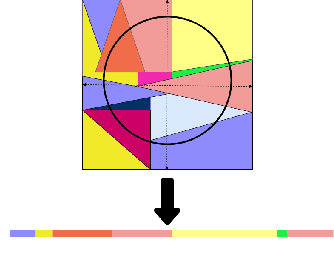
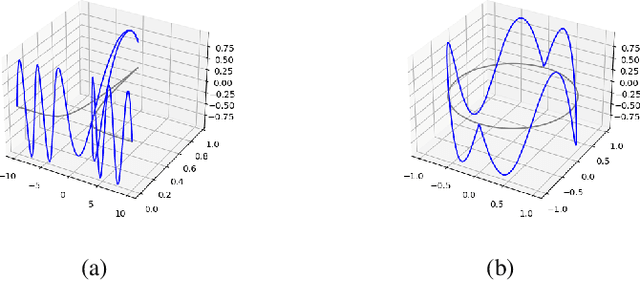
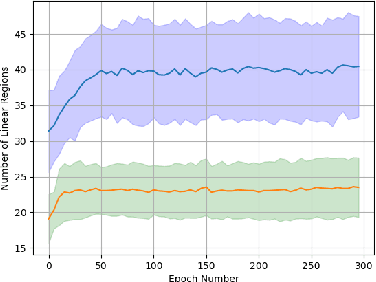
Abstract:Deep neural networks can approximate functions on different types of data, from images to graphs, with varied underlying structure. This underlying structure can be viewed as the geometry of the data manifold. By extending recent advances in the theoretical understanding of neural networks, we study how a randomly initialized neural network with piece-wise linear activation splits the data manifold into regions where the neural network behaves as a linear function. We derive bounds on the density of boundary of linear regions and the distance to these boundaries on the data manifold. This leads to insights into the expressivity of randomly initialized deep neural networks on non-Euclidean data sets. We empirically corroborate our theoretical results using a toy supervised learning problem. Our experiments demonstrate that number of linear regions varies across manifolds and the results hold with changing neural network architectures. We further demonstrate how the complexity of linear regions is different on the low dimensional manifold of images as compared to the Euclidean space, using the MetFaces dataset.
On the Geometry of Reinforcement Learning in Continuous State and Action Spaces
Dec 29, 2022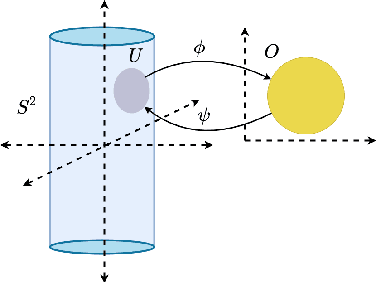

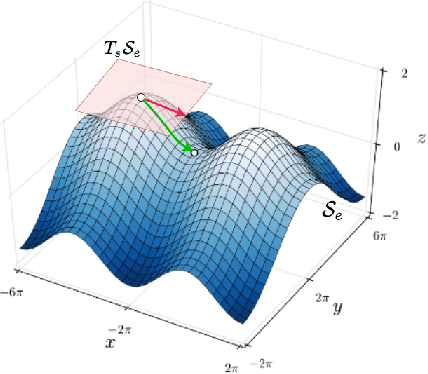
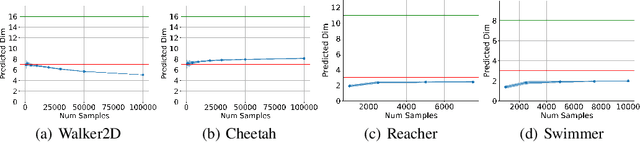
Abstract:Advances in reinforcement learning have led to its successful application in complex tasks with continuous state and action spaces. Despite these advances in practice, most theoretical work pertains to finite state and action spaces. We propose building a theoretical understanding of continuous state and action spaces by employing a geometric lens. Central to our work is the idea that the transition dynamics induce a low dimensional manifold of reachable states embedded in the high-dimensional nominal state space. We prove that, under certain conditions, the dimensionality of this manifold is at most the dimensionality of the action space plus one. This is the first result of its kind, linking the geometry of the state space to the dimensionality of the action space. We empirically corroborate this upper bound for four MuJoCo environments. We further demonstrate the applicability of our result by learning a policy in this low dimensional representation. To do so we introduce an algorithm that learns a mapping to a low dimensional representation, as a narrow hidden layer of a deep neural network, in tandem with the policy using DDPG. Our experiments show that a policy learnt this way perform on par or better for four MuJoCo control suite tasks.
Meta-Learning Transferable Parameterized Skills
Jun 07, 2022



Abstract:We propose a novel parameterized skill-learning algorithm that aims to learn transferable parameterized skills and synthesize them into a new action space that supports efficient learning in long-horizon tasks. We first propose novel learning objectives -- trajectory-centric diversity and smoothness -- that allow an agent to meta-learn reusable parameterized skills. Our agent can use these learned skills to construct a temporally-extended parameterized-action Markov decision process, for which we propose a hierarchical actor-critic algorithm that aims to efficiently learn a high-level control policy with the learned skills. We empirically demonstrate that the proposed algorithms enable an agent to solve a complicated long-horizon obstacle-course environment.
Natural Option Critic
Dec 04, 2018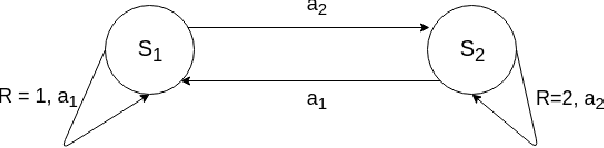
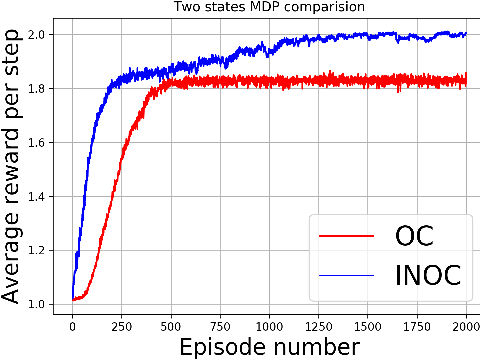
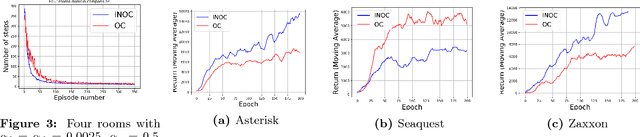
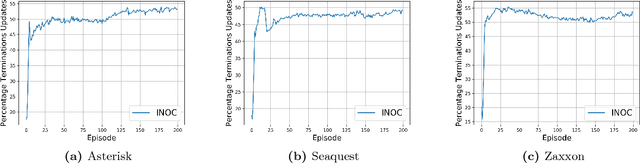
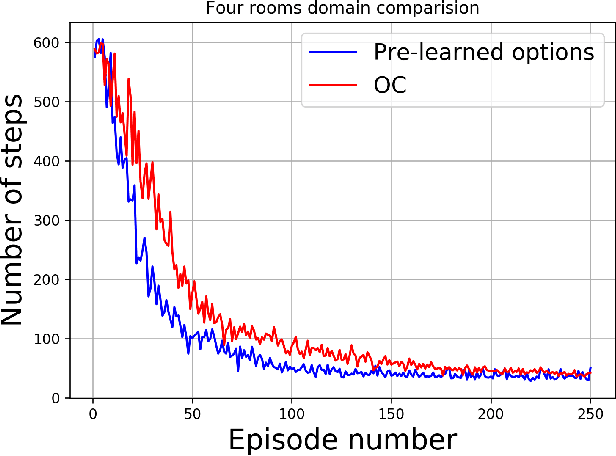
Abstract:The recently proposed option-critic architecture Bacon et al. provide a stochastic policy gradient approach to hierarchical reinforcement learning. Specifically, they provide a way to estimate the gradient of the expected discounted return with respect to parameters that define a finite number of temporally extended actions, called \textit{options}. In this paper we show how the option-critic architecture can be extended to estimate the natural gradient of the expected discounted return. To this end, the central questions that we consider in this paper are: 1) what is the definition of the natural gradient in this context, 2) what is the Fisher information matrix associated with an option's parameterized policy, 3) what is the Fisher information matrix associated with an option's parameterized termination function, and 4) how can a compatible function approximation approach be leveraged to obtain natural gradient estimates for both the parameterized policy and parameterized termination functions of an option with per-time-step time and space complexity linear in the total number of parameters. Based on answers to these questions we introduce the natural option critic algorithm. Experimental results showcase improvement over the vanilla gradient approach.
Hyperbolic Embeddings for Learning Options in Hierarchical Reinforcement Learning
Dec 04, 2018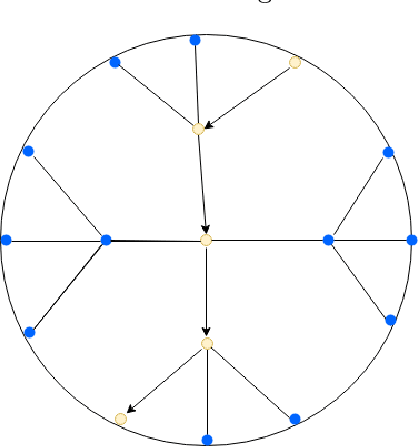

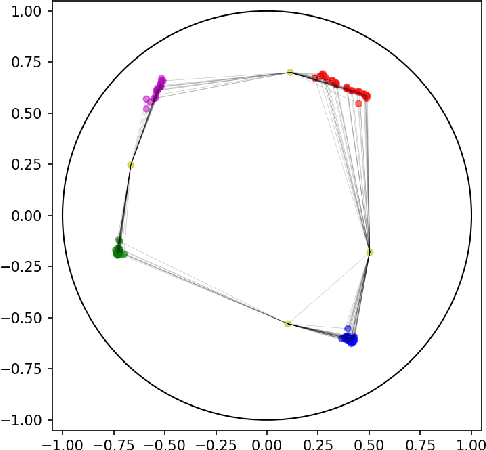
Abstract:Hierarchical reinforcement learning deals with the problem of breaking down large tasks into meaningful sub-tasks. Autonomous discovery of these sub-tasks has remained a challenging problem. We propose a novel method of learning sub-tasks by combining paradigms of routing in computer networks and graph based skill discovery within the options framework to define meaningful sub-goals. We apply the recent advancements of learning embeddings using Riemannian optimisation in the hyperbolic space to embed the state set into the hyperbolic space and create a model of the environment. In doing so we enforce a global topology on the states and are able to exploit this topology to learn meaningful sub-tasks. We demonstrate empirically, both in discrete and continuous domains, how these embeddings can improve the learning of meaningful sub-tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge