Natural Option Critic
Paper and Code
Dec 04, 2018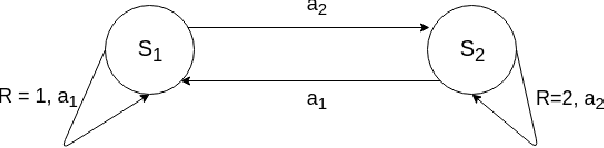
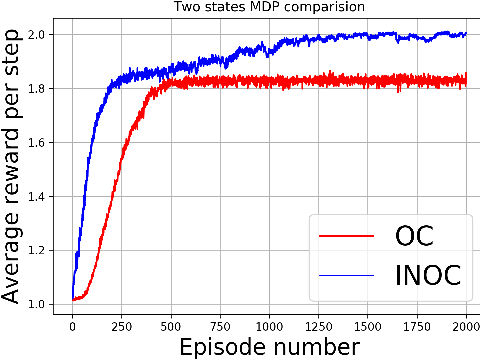
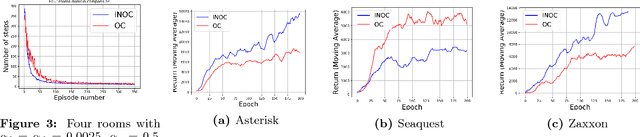
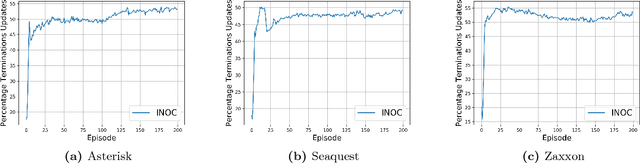
The recently proposed option-critic architecture Bacon et al. provide a stochastic policy gradient approach to hierarchical reinforcement learning. Specifically, they provide a way to estimate the gradient of the expected discounted return with respect to parameters that define a finite number of temporally extended actions, called \textit{options}. In this paper we show how the option-critic architecture can be extended to estimate the natural gradient of the expected discounted return. To this end, the central questions that we consider in this paper are: 1) what is the definition of the natural gradient in this context, 2) what is the Fisher information matrix associated with an option's parameterized policy, 3) what is the Fisher information matrix associated with an option's parameterized termination function, and 4) how can a compatible function approximation approach be leveraged to obtain natural gradient estimates for both the parameterized policy and parameterized termination functions of an option with per-time-step time and space complexity linear in the total number of parameters. Based on answers to these questions we introduce the natural option critic algorithm. Experimental results showcase improvement over the vanilla gradient approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge