Differentially Private Synthetic High-dimensional Tabular Stream

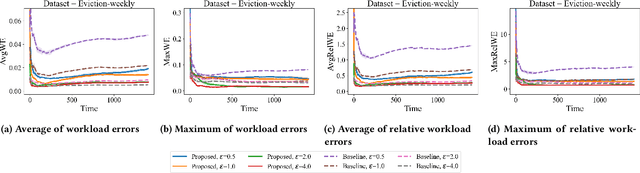
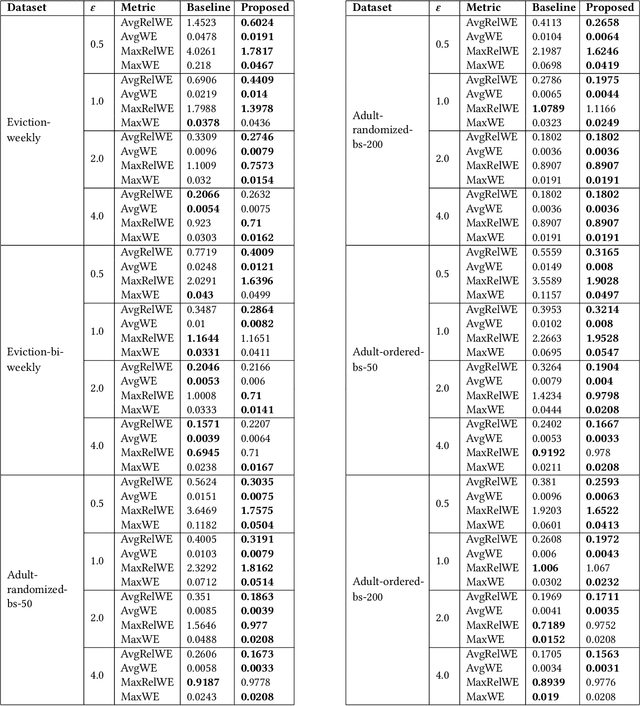
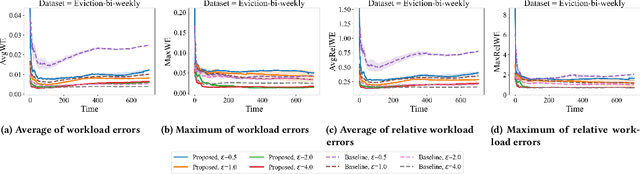
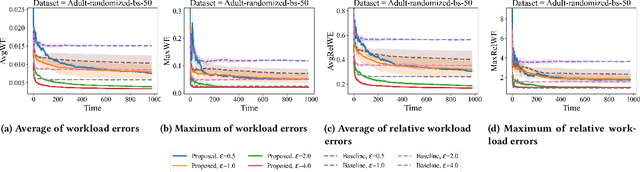
While differentially private synthetic data generation has been explored extensively in the literature, how to update this data in the future if the underlying private data changes is much less understood. We propose an algorithmic framework for streaming data that generates multiple synthetic datasets over time, tracking changes in the underlying private data. Our algorithm satisfies differential privacy for the entire input stream (continual differential privacy) and can be used for high-dimensional tabular data. Furthermore, we show the utility of our method via experiments on real-world datasets. The proposed algorithm builds upon a popular select, measure, fit, and iterate paradigm (used by offline synthetic data generation algorithms) and private counters for streams.

Online Differentially Private Synthetic Data Generation

We present a polynomial-time algorithm for online differentially private synthetic data generation. For a data stream within the hypercube $[0,1]^d$ and an infinite time horizon, we develop an online algorithm that generates a differentially private synthetic dataset at each time $t$. This algorithm achieves a near-optimal accuracy bound of $O(t^{-1/d}\log(t))$ for $d\geq 2$ and $O(t^{-1}\log^{4.5}(t))$ for $d=1$ in the 1-Wasserstein distance. This result generalizes the previous work on the continual release model for counting queries to include Lipschitz queries. Compared to the offline case, where the entire dataset is available at once, our approach requires only an extra polylog factor in the accuracy bound.

An Algorithm for Streaming Differentially Private Data

Much of the research in differential privacy has focused on offline applications with the assumption that all data is available at once. When these algorithms are applied in practice to streams where data is collected over time, this either violates the privacy guarantees or results in poor utility. We derive an algorithm for differentially private synthetic streaming data generation, especially curated towards spatial datasets. Furthermore, we provide a general framework for online selective counting among a collection of queries which forms a basis for many tasks such as query answering and synthetic data generation. The utility of our algorithm is verified on both real-world and simulated datasets.

Differentially private low-dimensional representation of high-dimensional data

Differentially private synthetic data provide a powerful mechanism to enable data analysis while protecting sensitive information about individuals. However, when the data lie in a high-dimensional space, the accuracy of the synthetic data suffers from the curse of dimensionality. In this paper, we propose a differentially private algorithm to generate low-dimensional synthetic data efficiently from a high-dimensional dataset with a utility guarantee with respect to the Wasserstein distance. A key step of our algorithm is a private principal component analysis (PCA) procedure with a near-optimal accuracy bound that circumvents the curse of dimensionality. Different from the standard perturbation analysis using the Davis-Kahan theorem, our analysis of private PCA works without assuming the spectral gap for the sample covariance matrix.

AVIDA: Alternating method for Visualizing and Integrating Data

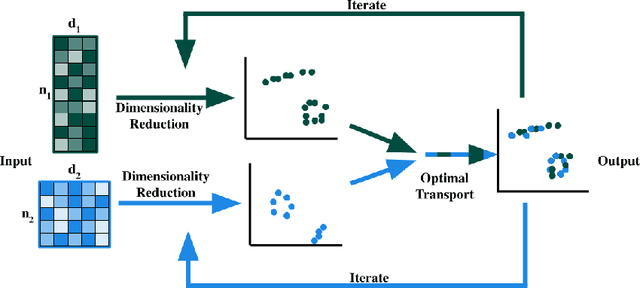
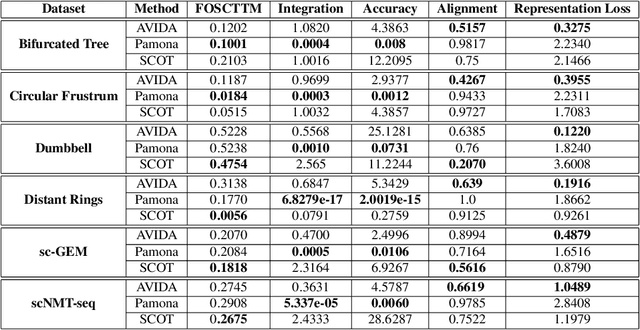
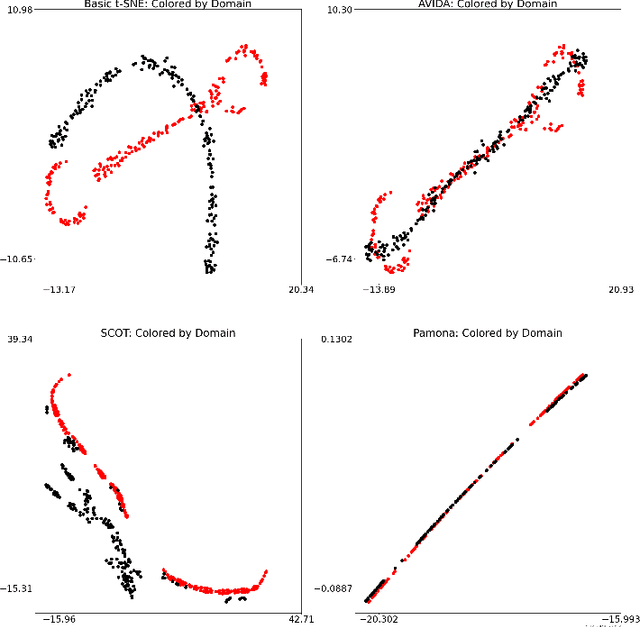
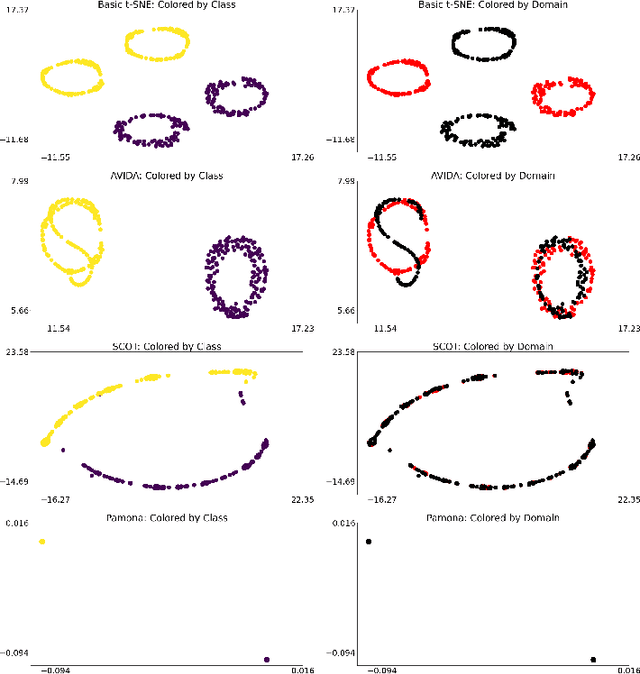
High-dimensional multimodal data arises in many scientific fields. The integration of multimodal data becomes challenging when there is no known correspondence between the samples and the features of different datasets. To tackle this challenge, we introduce AVIDA, a framework for simultaneously performing data alignment and dimension reduction. In the numerical experiments, Gromov-Wasserstein optimal transport and t-distributed stochastic neighbor embedding are used as the alignment and dimension reduction modules respectively. We show that AVIDA correctly aligns high-dimensional datasets without common features with four synthesized datasets and two real multimodal single-cell datasets. Compared to several existing methods, we demonstrate that AVIDA better preserves structures of individual datasets, especially distinct local structures in the joint low-dimensional visualization, while achieving comparable alignment performance. Such a property is important in multimodal single-cell data analysis as some biological processes are uniquely captured by one of the datasets. In general applications, other methods can be used for the alignment and dimension reduction modules.

The Quarks of Attention

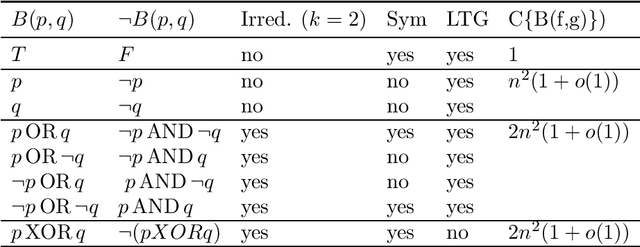
Attention plays a fundamental role in both natural and artificial intelligence systems. In deep learning, attention-based neural architectures, such as transformer architectures, are widely used to tackle problems in natural language processing and beyond. Here we investigate the fundamental building blocks of attention and their computational properties. Within the standard model of deep learning, we classify all possible fundamental building blocks of attention in terms of their source, target, and computational mechanism. We identify and study three most important mechanisms: additive activation attention, multiplicative output attention (output gating), and multiplicative synaptic attention (synaptic gating). The gating mechanisms correspond to multiplicative extensions of the standard model and are used across all current attention-based deep learning architectures. We study their functional properties and estimate the capacity of several attentional building blocks in the case of linear and polynomial threshold gates. Surprisingly, additive activation attention plays a central role in the proofs of the lower bounds. Attention mechanisms reduce the depth of certain basic circuits and leverage the power of quadratic activations without incurring their full cost.

A theory of capacity and sparse neural encoding

Motivated by biological considerations, we study sparse neural maps from an input layer to a target layer with sparse activity, and specifically the problem of storing $K$ input-target associations $(x,y)$, or memories, when the target vectors $y$ are sparse. We mathematically prove that $K$ undergoes a phase transition and that in general, and somewhat paradoxically, sparsity in the target layers increases the storage capacity of the map. The target vectors can be chosen arbitrarily, including in random fashion, and the memories can be both encoded and decoded by networks trained using local learning rules, including the simple Hebb rule. These results are robust under a variety of statistical assumptions on the data. The proofs rely on elegant properties of random polytopes and sub-gaussian random vector variables. Open problems and connections to capacity theories and polynomial threshold maps are discussed.

Memory capacity of neural networks with threshold and ReLU activations

Overwhelming theoretical and empirical evidence shows that mildly overparametrized neural networks -- those with more connections than the size of the training data -- are often able to memorize the training data with $100\%$ accuracy. This was rigorously proved for networks with sigmoid activation functions and, very recently, for ReLU activations. Addressing a 1988 open question of Baum, we prove that this phenomenon holds for general multilayered perceptrons, i.e. neural networks with threshold activation functions, or with any mix of threshold and ReLU activations. Our construction is probabilistic and exploits sparsity.

Online Stochastic Gradient Descent with Arbitrary Initialization Solves Non-smooth, Non-convex Phase Retrieval

In recent literature, a general two step procedure has been formulated for solving the problem of phase retrieval. First, a spectral technique is used to obtain a constant-error initial estimate, following which, the estimate is refined to arbitrary precision by first-order optimization of a non-convex loss function. Numerical experiments, however, seem to suggest that simply running the iterative schemes from a random initialization may also lead to convergence, albeit at the cost of slightly higher sample complexity. In this paper, we prove that, in fact, constant step size online stochastic gradient descent (SGD) converges from arbitrary initializations for the non-smooth, non-convex amplitude squared loss objective. In this setting, online SGD is also equivalent to the randomized Kaczmarz algorithm from numerical analysis. Our analysis can easily be generalized to other single index models. It also makes use of new ideas from stochastic process theory, including the notion of a summary state space, which we believe will be of use for the broader field of non-convex optimization.

The capacity of feedforward neural networks

A long standing open problem in the theory of neural networks is the development of quantitative methods to estimate and compare the capabilities of different architectures. Here we define the capacity of an architecture by the binary logarithm of the number of functions it can compute, as the synaptic weights are varied. The capacity is an upper bound on the number of bits that can be "communicated" from the training data to the architecture over the learning channel. We study the capacity of layered, fully-connected, architectures of linear threshold neurons with $L$ layers of size $n_1,n_2, \ldots, n_L$ and show that in essence the capacity is given by a cubic polynomial in the layer sizes: $C(n_1,\ldots, n_L)=\sum_{k=1}^{L-1} \min(n_1,\ldots,n_k)n_kn_{k+1}$. In proving the main result, we also develop new techniques (multiplexing, enrichment, and stacking) as well as new bounds on the capacity of finite sets. We use the main result to identify architectures with maximal or minimal capacity under a number of natural constraints. This leads to the notion of structural regularization for deep architectures. While in general, everything else being equal, shallow networks compute more functions than deep networks, the functions computed by deep networks are more regular and "interesting".