AVIDA: Alternating method for Visualizing and Integrating Data
Paper and Code
May 31, 2022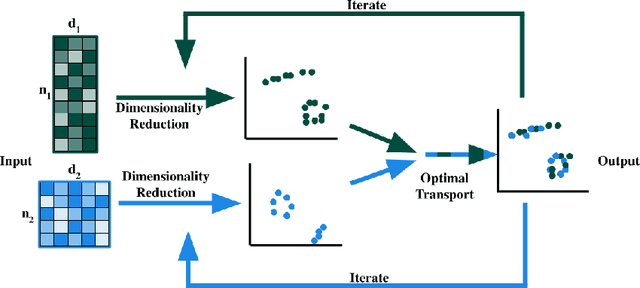
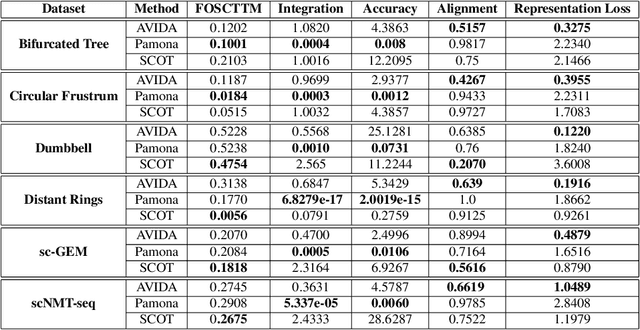
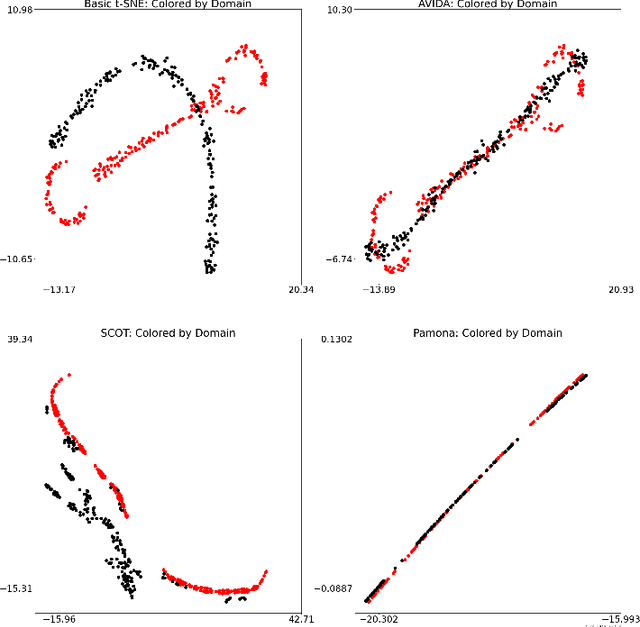
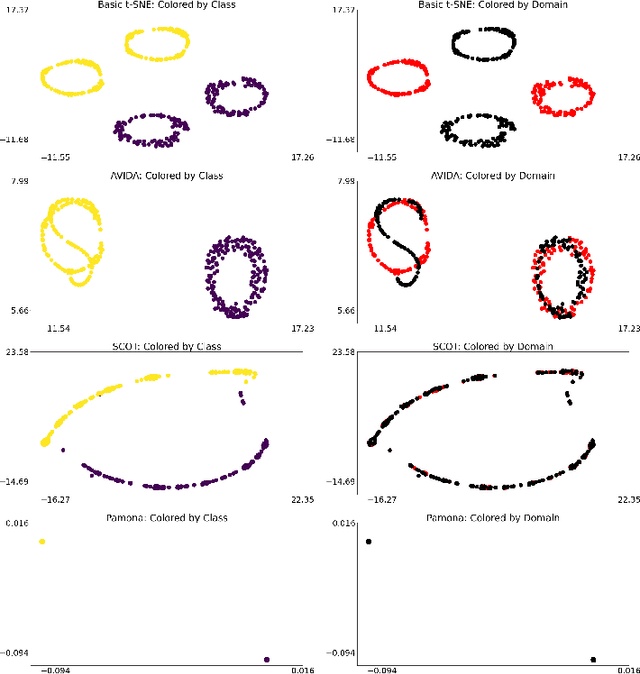
High-dimensional multimodal data arises in many scientific fields. The integration of multimodal data becomes challenging when there is no known correspondence between the samples and the features of different datasets. To tackle this challenge, we introduce AVIDA, a framework for simultaneously performing data alignment and dimension reduction. In the numerical experiments, Gromov-Wasserstein optimal transport and t-distributed stochastic neighbor embedding are used as the alignment and dimension reduction modules respectively. We show that AVIDA correctly aligns high-dimensional datasets without common features with four synthesized datasets and two real multimodal single-cell datasets. Compared to several existing methods, we demonstrate that AVIDA better preserves structures of individual datasets, especially distinct local structures in the joint low-dimensional visualization, while achieving comparable alignment performance. Such a property is important in multimodal single-cell data analysis as some biological processes are uniquely captured by one of the datasets. In general applications, other methods can be used for the alignment and dimension reduction modules.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge