LEARNER: Learning Granular Labels from Coarse Labels using Contrastive Learning

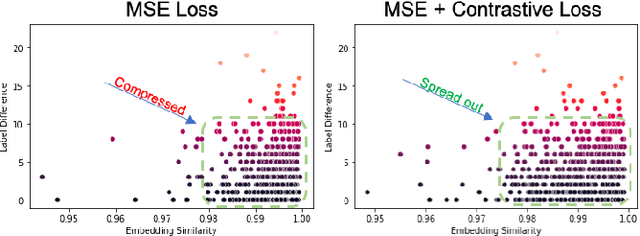
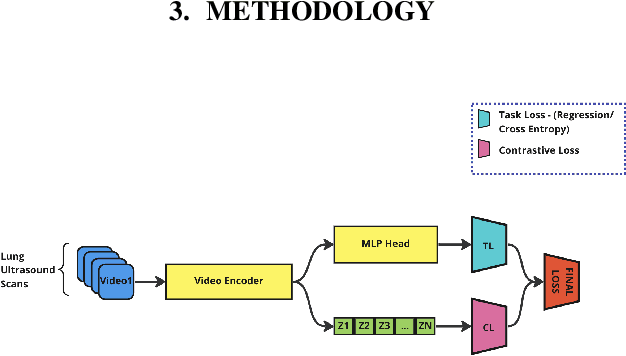
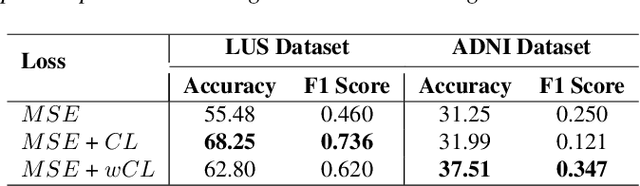
A crucial question in active patient care is determining if a treatment is having the desired effect, especially when changes are subtle over short periods. We propose using inter-patient data to train models that can learn to detect these fine-grained changes within a single patient. Specifically, can a model trained on multi-patient scans predict subtle changes in an individual patient's scans? Recent years have seen increasing use of deep learning (DL) in predicting diseases using biomedical imaging, such as predicting COVID-19 severity using lung ultrasound (LUS) data. While extensive literature exists on successful applications of DL systems when well-annotated large-scale datasets are available, it is quite difficult to collect a large corpus of personalized datasets for an individual. In this work, we investigate the ability of recent computer vision models to learn fine-grained differences while being trained on data showing larger differences. We evaluate on an in-house LUS dataset and a public ADNI brain MRI dataset. We find that models pre-trained on clips from multiple patients can better predict fine-grained differences in scans from a single patient by employing contrastive learning.

Federated Minimax Optimization with Client Heterogeneity

Minimax optimization has seen a surge in interest with the advent of modern applications such as GANs, and it is inherently more challenging than simple minimization. The difficulty is exacerbated by the training data residing at multiple edge devices or \textit{clients}, especially when these clients can have heterogeneous datasets and local computation capabilities. We propose a general federated minimax optimization framework that subsumes such settings and several existing methods like Local SGDA. We show that naive aggregation of heterogeneous local progress results in optimizing a mismatched objective function -- a phenomenon previously observed in standard federated minimization. To fix this problem, we propose normalizing the client updates by the number of local steps undertaken between successive communication rounds. We analyze the convergence of the proposed algorithm for classes of nonconvex-concave and nonconvex-nonconcave functions and characterize the impact of heterogeneous client data, partial client participation, and heterogeneous local computations. Our analysis works under more general assumptions on the intra-client noise and inter-client heterogeneity than so far considered in the literature. For all the function classes considered, we significantly improve the existing computation and communication complexity results. Experimental results support our theoretical claims.

Federated Minimax Optimization: Improved Convergence Analyses and Algorithms

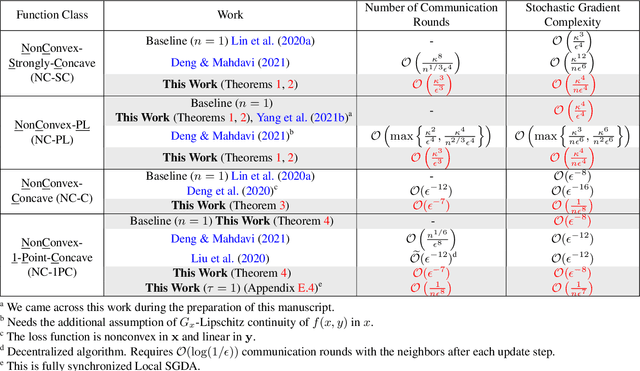
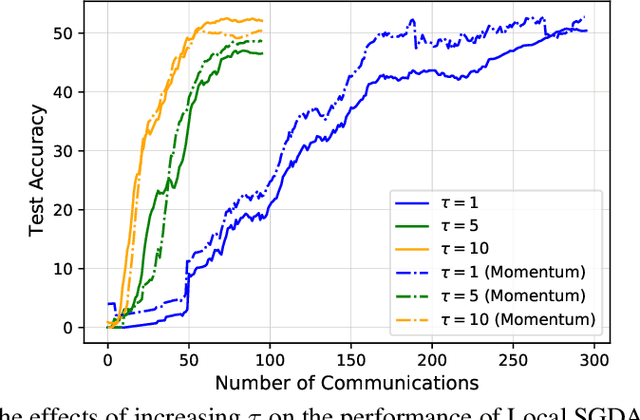
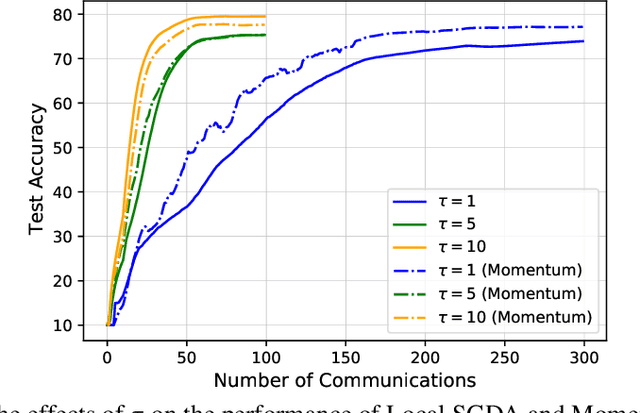
In this paper, we consider nonconvex minimax optimization, which is gaining prominence in many modern machine learning applications such as GANs. Large-scale edge-based collection of training data in these applications calls for communication-efficient distributed optimization algorithms, such as those used in federated learning, to process the data. In this paper, we analyze Local stochastic gradient descent ascent (SGDA), the local-update version of the SGDA algorithm. SGDA is the core algorithm used in minimax optimization, but it is not well-understood in a distributed setting. We prove that Local SGDA has \textit{order-optimal} sample complexity for several classes of nonconvex-concave and nonconvex-nonconcave minimax problems, and also enjoys \textit{linear speedup} with respect to the number of clients. We provide a novel and tighter analysis, which improves the convergence and communication guarantees in the existing literature. For nonconvex-PL and nonconvex-one-point-concave functions, we improve the existing complexity results for centralized minimax problems. Furthermore, we propose a momentum-based local-update algorithm, which has the same convergence guarantees, but outperforms Local SGDA as demonstrated in our experiments.