Federated Minimax Optimization: Improved Convergence Analyses and Algorithms
Paper and Code
Mar 09, 2022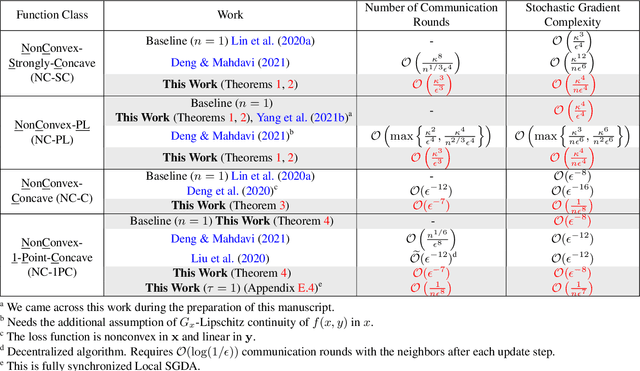
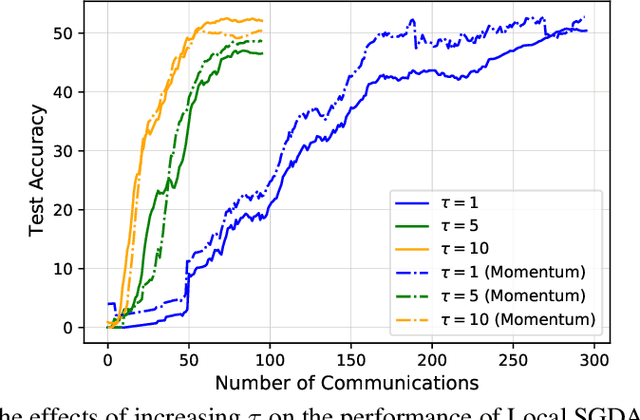
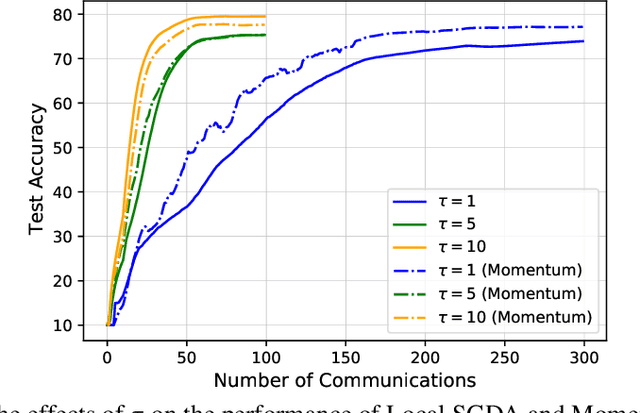

In this paper, we consider nonconvex minimax optimization, which is gaining prominence in many modern machine learning applications such as GANs. Large-scale edge-based collection of training data in these applications calls for communication-efficient distributed optimization algorithms, such as those used in federated learning, to process the data. In this paper, we analyze Local stochastic gradient descent ascent (SGDA), the local-update version of the SGDA algorithm. SGDA is the core algorithm used in minimax optimization, but it is not well-understood in a distributed setting. We prove that Local SGDA has \textit{order-optimal} sample complexity for several classes of nonconvex-concave and nonconvex-nonconcave minimax problems, and also enjoys \textit{linear speedup} with respect to the number of clients. We provide a novel and tighter analysis, which improves the convergence and communication guarantees in the existing literature. For nonconvex-PL and nonconvex-one-point-concave functions, we improve the existing complexity results for centralized minimax problems. Furthermore, we propose a momentum-based local-update algorithm, which has the same convergence guarantees, but outperforms Local SGDA as demonstrated in our experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge