Robert H. Aseltine
Salvaging Forbidden Treasure in Medical Data: Utilizing Surrogate Outcomes and Single Records for Rare Event Modeling
Jan 25, 2025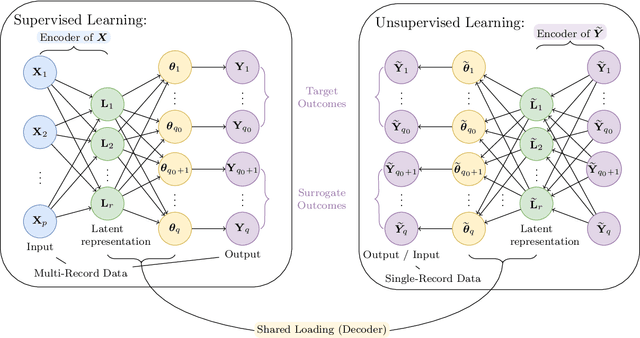
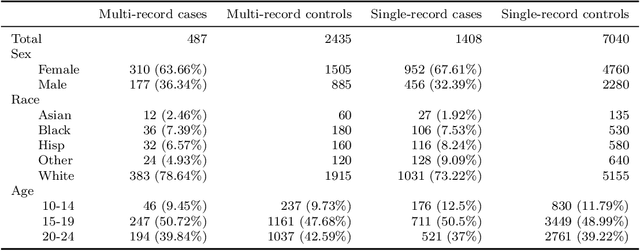
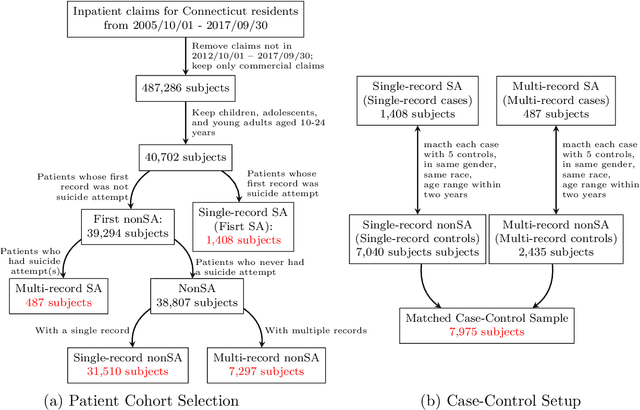

Abstract:The vast repositories of Electronic Health Records (EHR) and medical claims hold untapped potential for studying rare but critical events, such as suicide attempt. Conventional setups often model suicide attempt as a univariate outcome and also exclude any ``single-record'' patients with a single documented encounter due to a lack of historical information. However, patients who were diagnosed with suicide attempts at the only encounter could, to some surprise, represent a substantial proportion of all attempt cases in the data, as high as 70--80%. We innovate a hybrid and integrative learning framework to leverage concurrent outcomes as surrogates and harness the forbidden yet precious information from single-record data. Our approach employs a supervised learning component to learn the latent variables that connect primary (e.g., suicide) and surrogate outcomes (e.g., mental disorders) to historical information. It simultaneously employs an unsupervised learning component to utilize the single-record data, through the shared latent variables. As such, our approach offers a general strategy for information integration that is crucial to modeling rare conditions and events. With hospital inpatient data from Connecticut, we demonstrate that single-record data and concurrent diagnoses indeed carry valuable information, and utilizing them can substantially improve suicide risk modeling.
Tree-Guided Rare Feature Selection and Logic Aggregation with Electronic Health Records Data
Jun 18, 2022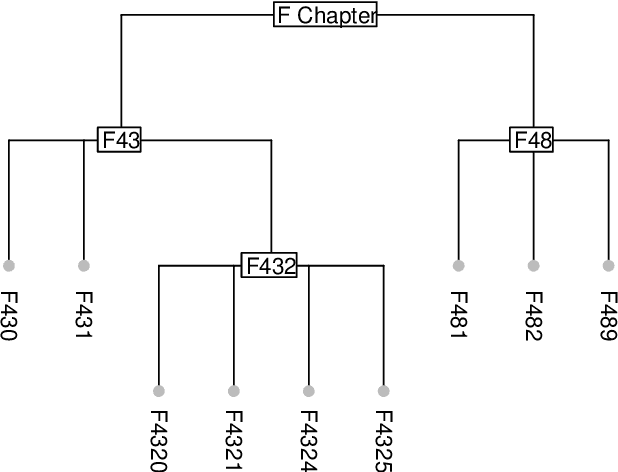
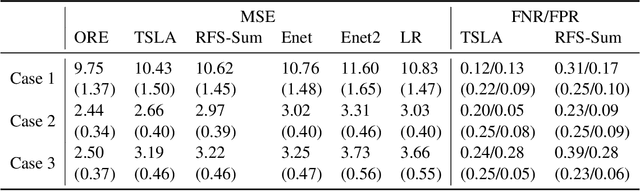
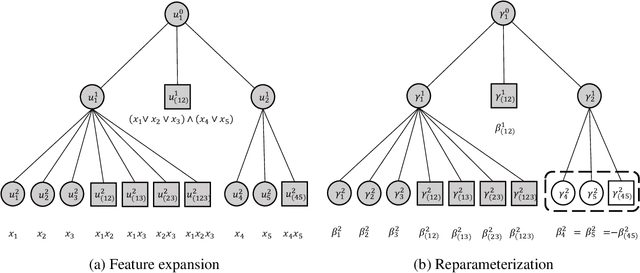
Abstract:Statistical learning with a large number of rare binary features is commonly encountered in analyzing electronic health records (EHR) data, especially in the modeling of disease onset with prior medical diagnoses and procedures. Dealing with the resulting highly sparse and large-scale binary feature matrix is notoriously challenging as conventional methods may suffer from a lack of power in testing and inconsistency in model fitting while machine learning methods may suffer from the inability of producing interpretable results or clinically-meaningful risk factors. To improve EHR-based modeling and utilize the natural hierarchical structure of disease classification, we propose a tree-guided feature selection and logic aggregation approach for large-scale regression with rare binary features, in which dimension reduction is achieved through not only a sparsity pursuit but also an aggregation promoter with the logic operator of ``or''. We convert the combinatorial problem into a convex linearly-constrained regularized estimation, which enables scalable computation with theoretical guarantees. In a suicide risk study with EHR data, our approach is able to select and aggregate prior mental health diagnoses as guided by the diagnosis hierarchy of the International Classification of Diseases. By balancing the rarity and specificity of the EHR diagnosis records, our strategy improves both prediction and model interpretation. We identify important higher-level categories and subcategories of mental health conditions and simultaneously determine the level of specificity needed for each of them in predicting suicide risk.
Suicide Risk Modeling with Uncertain Diagnostic Records
Sep 05, 2020
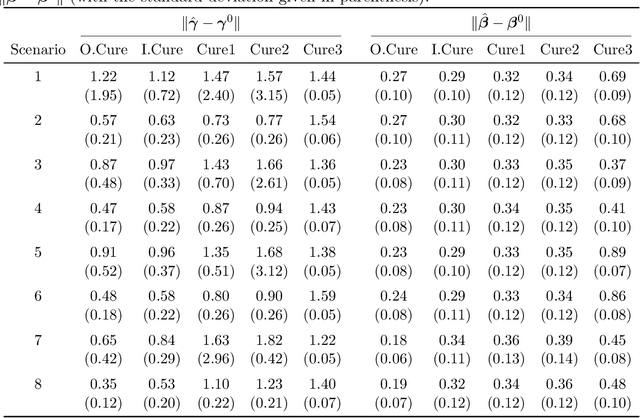
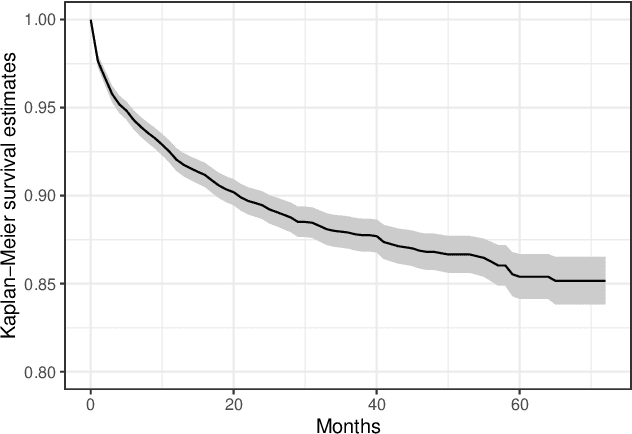
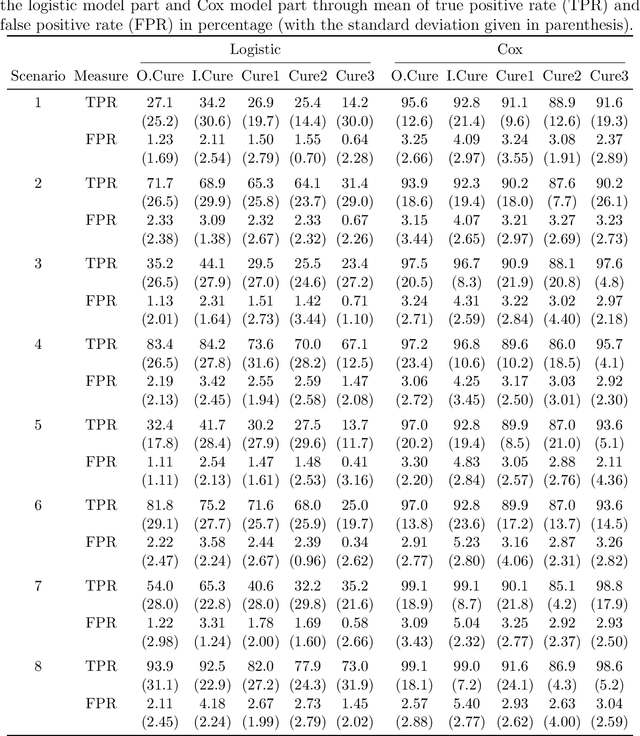
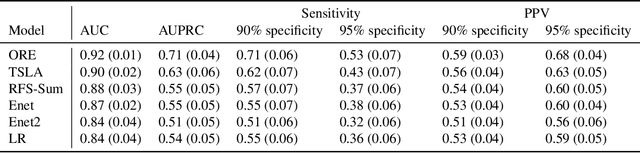
Abstract:Motivated by the pressing need for suicide prevention through improving behavioral healthcare, we use medical claims data to study the risk of subsequent suicide attempts for patients who were hospitalized due to suicide attempts and later discharged. Understanding the risk behaviors of such patients at elevated suicide risk is an important step towards the goal of "Zero Suicide". An immediate and unconventional challenge is that the identification of suicide attempts from medical claims contains substantial uncertainty: almost 20\% of "suspected" suicide attempts are identified from diagnostic codes indicating external causes of injury and poisoning with undermined intent. It is thus of great interest to learn which of these undetermined events are more likely actual suicide attempts and how to properly utilize them in survival analysis with severe censoring. To tackle these interrelated problems, we develop an integrative Cox cure model with regularization to perform survival regression with uncertain events and a latent cure fraction. We apply the proposed approach to study the risk of subsequent suicide attempt after suicide-related hospitalization for adolescent and young adult population, using medical claims data from Connecticut. The identified risk factors are highly interpretable; more intriguingly, our method distinguishes the risk factors that are most helpful in assessing either susceptibility or timing of subsequent attempt. The predicted statuses of the uncertain attempts are further investigated, leading to several new insights on suicide event identification.
Pursuing Sources of Heterogeneity in Modeling Clustered Population
Mar 10, 2020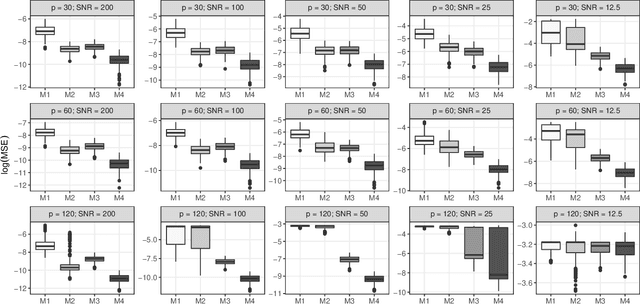
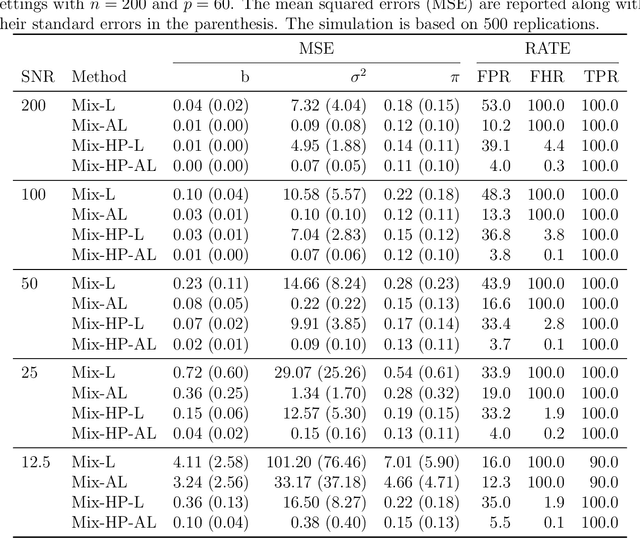
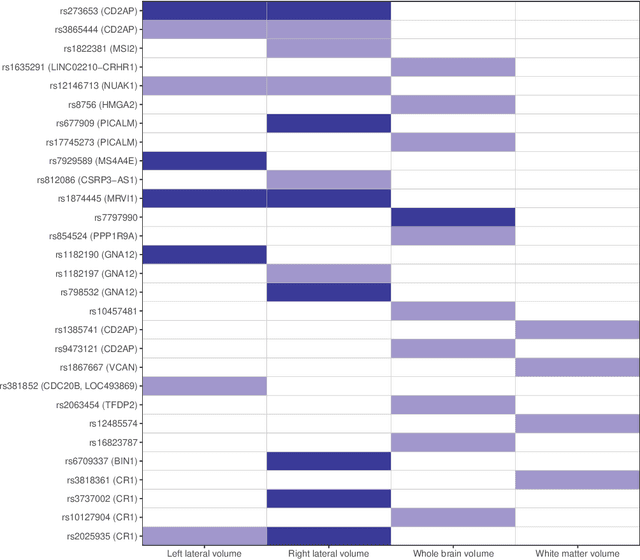

Abstract:Researchers often have to deal with heterogeneous population with mixed regression relationships, increasingly so in the era of data explosion. In such problems, when there are many candidate predictors, it is not only of interest to identify the predictors that are associated with the outcome, but also to distinguish the true sources of heterogeneity, i.e., to identify the predictors that have different effects among the clusters and thus are the true contributors to the formation of the clusters. We clarify the concepts of the source of heterogeneity that account for potential scale differences of the clusters and propose a regularized finite mixture effects regression to achieve heterogeneity pursuit and feature selection simultaneously. As the name suggests, the problem is formulated under an effects-model parameterization, in which the cluster labels are missing and the effect of each predictor on the outcome is decomposed to a common effect term and a set of cluster-specific terms. A constrained sparse estimation of these effects leads to the identification of both the variables with common effects and those with heterogeneous effects. We propose an efficient algorithm and show that our approach can achieve both estimation and selection consistency. Simulation studies further demonstrate the effectiveness of our method under various practical scenarios. Three applications are presented, namely, an imaging genetics study for linking genetic factors and brain neuroimaging traits in Alzheimer's disease, a public health study for exploring the association between suicide risk among adolescents and their school district characteristics, and a sport analytics study for understanding how the salary levels of baseball players are associated with their performance and contractual status.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge