Tree-Guided Rare Feature Selection and Logic Aggregation with Electronic Health Records Data
Paper and Code
Jun 18, 2022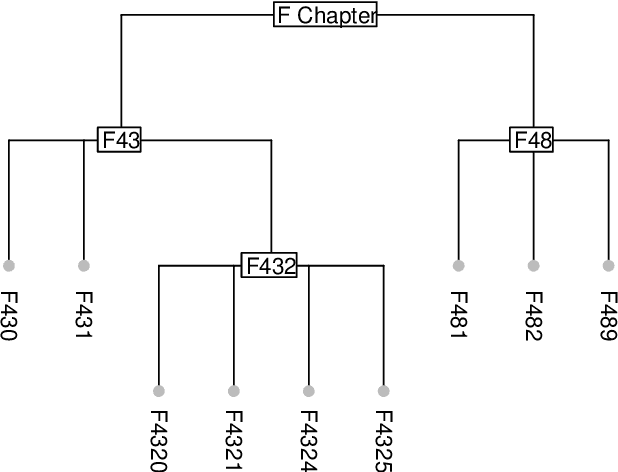
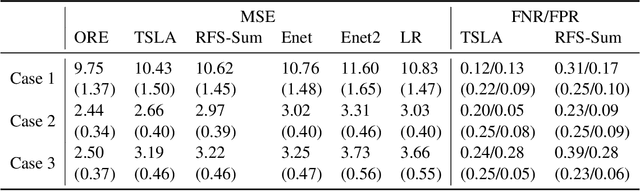
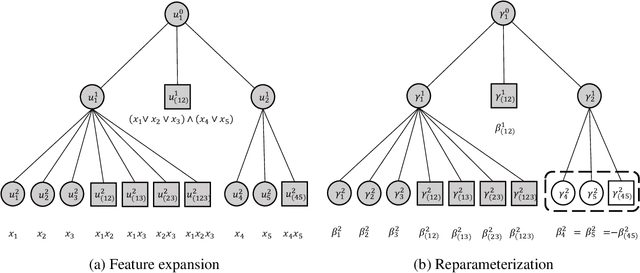
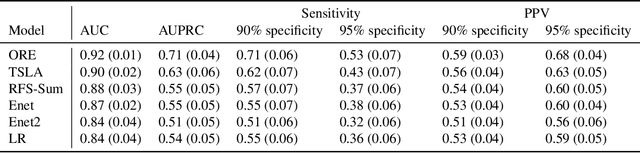
Statistical learning with a large number of rare binary features is commonly encountered in analyzing electronic health records (EHR) data, especially in the modeling of disease onset with prior medical diagnoses and procedures. Dealing with the resulting highly sparse and large-scale binary feature matrix is notoriously challenging as conventional methods may suffer from a lack of power in testing and inconsistency in model fitting while machine learning methods may suffer from the inability of producing interpretable results or clinically-meaningful risk factors. To improve EHR-based modeling and utilize the natural hierarchical structure of disease classification, we propose a tree-guided feature selection and logic aggregation approach for large-scale regression with rare binary features, in which dimension reduction is achieved through not only a sparsity pursuit but also an aggregation promoter with the logic operator of ``or''. We convert the combinatorial problem into a convex linearly-constrained regularized estimation, which enables scalable computation with theoretical guarantees. In a suicide risk study with EHR data, our approach is able to select and aggregate prior mental health diagnoses as guided by the diagnosis hierarchy of the International Classification of Diseases. By balancing the rarity and specificity of the EHR diagnosis records, our strategy improves both prediction and model interpretation. We identify important higher-level categories and subcategories of mental health conditions and simultaneously determine the level of specificity needed for each of them in predicting suicide risk.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge