Pursuing Sources of Heterogeneity in Modeling Clustered Population
Paper and Code
Mar 10, 2020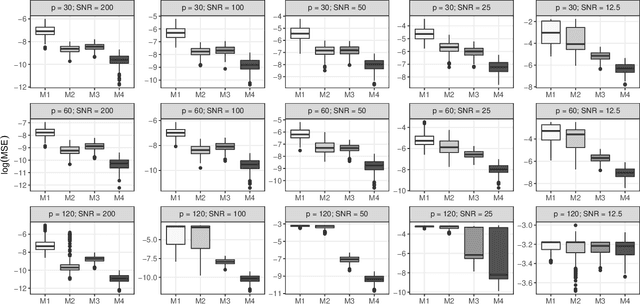
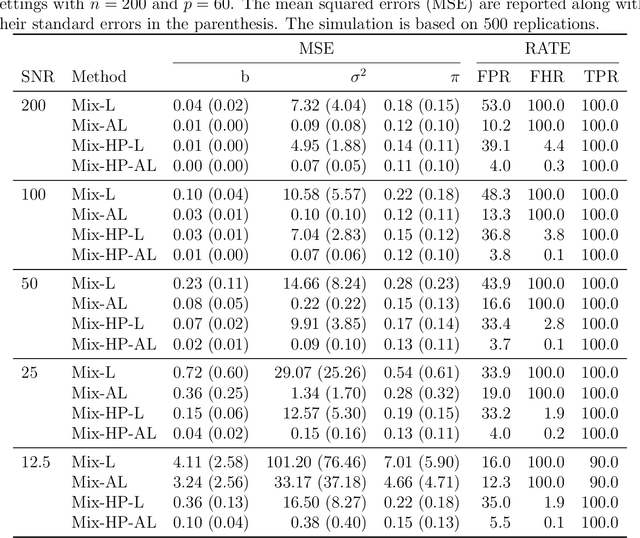
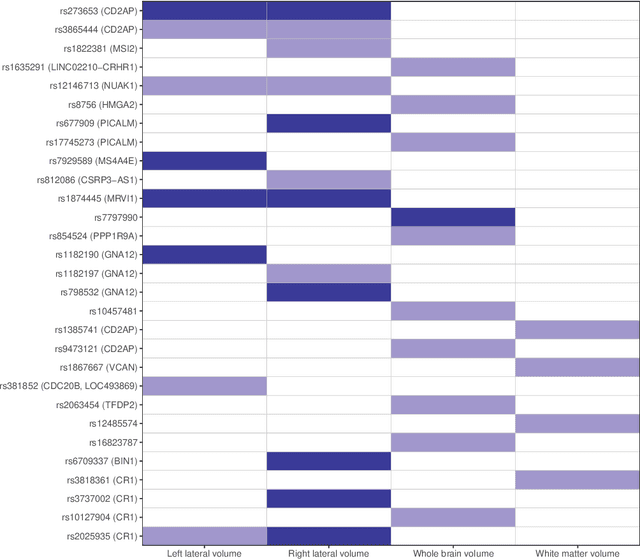

Researchers often have to deal with heterogeneous population with mixed regression relationships, increasingly so in the era of data explosion. In such problems, when there are many candidate predictors, it is not only of interest to identify the predictors that are associated with the outcome, but also to distinguish the true sources of heterogeneity, i.e., to identify the predictors that have different effects among the clusters and thus are the true contributors to the formation of the clusters. We clarify the concepts of the source of heterogeneity that account for potential scale differences of the clusters and propose a regularized finite mixture effects regression to achieve heterogeneity pursuit and feature selection simultaneously. As the name suggests, the problem is formulated under an effects-model parameterization, in which the cluster labels are missing and the effect of each predictor on the outcome is decomposed to a common effect term and a set of cluster-specific terms. A constrained sparse estimation of these effects leads to the identification of both the variables with common effects and those with heterogeneous effects. We propose an efficient algorithm and show that our approach can achieve both estimation and selection consistency. Simulation studies further demonstrate the effectiveness of our method under various practical scenarios. Three applications are presented, namely, an imaging genetics study for linking genetic factors and brain neuroimaging traits in Alzheimer's disease, a public health study for exploring the association between suicide risk among adolescents and their school district characteristics, and a sport analytics study for understanding how the salary levels of baseball players are associated with their performance and contractual status.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge