Unifying Explainable Anomaly Detection and Root Cause Analysis in Dynamical Systems

Dynamical systems, prevalent in various scientific and engineering domains, are susceptible to anomalies that can significantly impact their performance and reliability. This paper addresses the critical challenges of anomaly detection, root cause localization, and anomaly type classification in dynamical systems governed by ordinary differential equations (ODEs). We define two categories of anomalies: cyber anomalies, which propagate through interconnected variables, and measurement anomalies, which remain localized to individual variables. To address these challenges, we propose the Interpretable Causality Ordinary Differential Equation (ICODE) Networks, a model-intrinsic explainable learning framework. ICODE leverages Neural ODEs for anomaly detection while employing causality inference through an explanation channel to perform root cause analysis (RCA), elucidating why specific time periods are flagged as anomalous. ICODE is designed to simultaneously perform anomaly detection, RCA, and anomaly type classification within a single, interpretable framework. Our approach is grounded in the hypothesis that anomalies alter the underlying ODEs of the system, manifesting as changes in causal relationships between variables. We provide a theoretical analysis of how perturbations in learned model parameters can be utilized to identify anomalies and their root causes in time series data. Comprehensive experimental evaluations demonstrate the efficacy of ICODE across various dynamical systems, showcasing its ability to accurately detect anomalies, classify their types, and pinpoint their origins.

Incorporating Domain Differential Equations into Graph Convolutional Networks to Lower Generalization Discrepancy

Ensuring both accuracy and robustness in time series prediction is critical to many applications, ranging from urban planning to pandemic management. With sufficient training data where all spatiotemporal patterns are well-represented, existing deep-learning models can make reasonably accurate predictions. However, existing methods fail when the training data are drawn from different circumstances (e.g., traffic patterns on regular days) compared to test data (e.g., traffic patterns after a natural disaster). Such challenges are usually classified under domain generalization. In this work, we show that one way to address this challenge in the context of spatiotemporal prediction is by incorporating domain differential equations into Graph Convolutional Networks (GCNs). We theoretically derive conditions where GCNs incorporating such domain differential equations are robust to mismatched training and testing data compared to baseline domain agnostic models. To support our theory, we propose two domain-differential-equation-informed networks called Reaction-Diffusion Graph Convolutional Network (RDGCN), which incorporates differential equations for traffic speed evolution, and Susceptible-Infectious-Recovered Graph Convolutional Network (SIRGCN), which incorporates a disease propagation model. Both RDGCN and SIRGCN are based on reliable and interpretable domain differential equations that allow the models to generalize to unseen patterns. We experimentally show that RDGCN and SIRGCN are more robust with mismatched testing data than the state-of-the-art deep learning methods.

Communication-Efficient {Federated} Learning Using Censored Heavy Ball Descent

Distributed machine learning enables scalability and computational offloading, but requires significant levels of communication. Consequently, communication efficiency in distributed learning settings is an important consideration, especially when the communications are wireless and battery-driven devices are employed. In this paper we develop a censoring-based heavy ball (CHB) method for distributed learning in a server-worker architecture. Each worker self-censors unless its local gradient is sufficiently different from the previously transmitted one. The significant practical advantages of the HB method for learning problems are well known, but the question of reducing communications has not been addressed. CHB takes advantage of the HB smoothing to eliminate reporting small changes, and provably achieves a linear convergence rate equivalent to that of the classical HB method for smooth and strongly convex objective functions. The convergence guarantee of CHB is theoretically justified for both convex and nonconvex cases. In addition we prove that, under some conditions, at least half of all communications can be eliminated without any impact on convergence rate. Extensive numerical results validate the communication efficiency of CHB on both synthetic and real datasets, for convex, nonconvex, and nondifferentiable cases. Given a target accuracy, CHB can significantly reduce the number of communications compared to existing algorithms, achieving the same accuracy without slowing down the optimization process.

Communication Efficient Federated Learning via Ordered ADMM in a Fully Decentralized Setting

The challenge of communication-efficient distributed optimization has attracted attention in recent years. In this paper, a communication efficient algorithm, called ordering-based alternating direction method of multipliers (OADMM) is devised in a general fully decentralized network setting where a worker can only exchange messages with neighbors. Compared to the classical ADMM, a key feature of OADMM is that transmissions are ordered among workers at each iteration such that a worker with the most informative data broadcasts its local variable to neighbors first, and neighbors who have not transmitted yet can update their local variables based on that received transmission. In OADMM, we prohibit workers from transmitting if their current local variables are not sufficiently different from their previously transmitted value. A variant of OADMM, called SOADMM, is proposed where transmissions are ordered but transmissions are never stopped for each node at each iteration. Numerical results demonstrate that given a targeted accuracy, OADMM can significantly reduce the number of communications compared to existing algorithms including ADMM. We also show numerically that SOADMM can accelerate convergence, resulting in communication savings compared to the classical ADMM.

Distributed Learning With Sparsified Gradient Differences

A very large number of communications are typically required to solve distributed learning tasks, and this critically limits scalability and convergence speed in wireless communications applications. In this paper, we devise a Gradient Descent method with Sparsification and Error Correction (GD-SEC) to improve the communications efficiency in a general worker-server architecture. Motivated by a variety of wireless communications learning scenarios, GD-SEC reduces the number of bits per communication from worker to server with no degradation in the order of the convergence rate. This enables larger-scale model learning without sacrificing convergence or accuracy. At each iteration of GD-SEC, instead of directly transmitting the entire gradient vector, each worker computes the difference between its current gradient and a linear combination of its previously transmitted gradients, and then transmits the sparsified gradient difference to the server. A key feature of GD-SEC is that any given component of the gradient difference vector will not be transmitted if its magnitude is not sufficiently large. An error correction technique is used at each worker to compensate for the error resulting from sparsification. We prove that GD-SEC is guaranteed to converge for strongly convex, convex, and nonconvex optimization problems with the same order of convergence rate as GD. Furthermore, if the objective function is strongly convex, GD-SEC has a fast linear convergence rate. Numerical results not only validate the convergence rate of GD-SEC but also explore the communication bit savings it provides. Given a target accuracy, GD-SEC can significantly reduce the communications load compared to the best existing algorithms without slowing down the optimization process.

Training Robust Graph Neural Networks with Topology Adaptive Edge Dropping

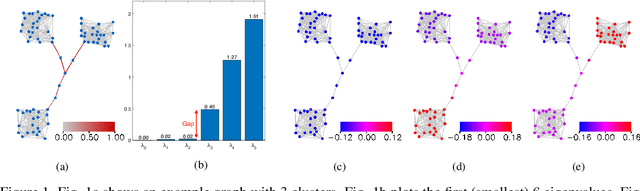
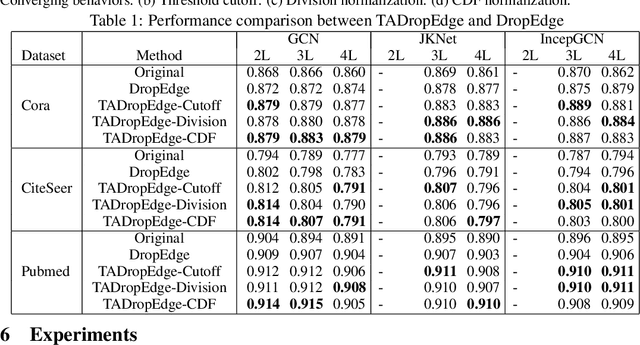
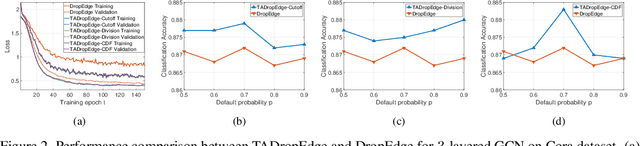
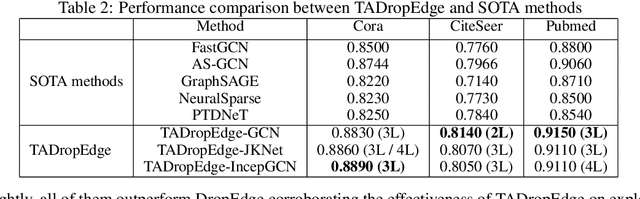
Graph neural networks (GNNs) are processing architectures that exploit graph structural information to model representations from network data. Despite their success, GNNs suffer from sub-optimal generalization performance given limited training data, referred to as over-fitting. This paper proposes Topology Adaptive Edge Dropping (TADropEdge) method as an adaptive data augmentation technique to improve generalization performance and learn robust GNN models. We start by explicitly analyzing how random edge dropping increases the data diversity during training, while indicating i.i.d. edge dropping does not account for graph structural information and could result in noisy augmented data degrading performance. To overcome this issue, we consider graph connectivity as the key property that captures graph topology. TADropEdge incorporates this factor into random edge dropping such that the edge-dropped subgraphs maintain similar topology as the underlying graph, yielding more satisfactory data augmentation. In particular, TADropEdge first leverages the graph spectrum to assign proper weights to graph edges, which represent their criticality for establishing the graph connectivity. It then normalizes the edge weights and drops graph edges adaptively based on their normalized weights. Besides improving generalization performance, TADropEdge reduces variance for efficient training and can be applied as a generic method modular to different GNN models. Intensive experiments on real-life and synthetic datasets corroborate theory and verify the effectiveness of the proposed method.

Sparse Representation based Multi-sensor Image Fusion: A Review

As a result of several successful applications in computer vision and image processing, sparse representation (SR) has attracted significant attention in multi-sensor image fusion. Unlike the traditional multiscale transforms (MSTs) that presume the basis functions, SR learns an over-complete dictionary from a set of training images for image fusion, and it achieves more stable and meaningful representations of the source images. By doing so, the SR-based fusion methods generally outperform the traditional MST-based image fusion methods in both subjective and objective tests. In addition, they are less susceptible to mis-registration among the source images, thus facilitating the practical applications. This survey paper proposes a systematic review of the SR-based multi-sensor image fusion literature, highlighting the pros and cons of each category of approaches. Specifically, we start by performing a theoretical investigation of the entire system from three key algorithmic aspects, (1) sparse representation models; (2) dictionary learning methods; and (3) activity levels and fusion rules. Subsequently, we show how the existing works address these scientific problems and design the appropriate fusion rules for each application, such as multi-focus image fusion and multi-modality (e.g., infrared and visible) image fusion. At last, we carry out some experiments to evaluate the impact of these three algorithmic components on the fusion performance when dealing with different applications. This article is expected to serve as a tutorial and source of reference for researchers preparing to enter the field or who desire to employ the sparse representation theory in other fields.