A Deep Learning Approach to Language-independent Gender Prediction on Twitter

This work presents a set of experiments conducted to predict the gender of Twitter users based on language-independent features extracted from the text of the users' tweets. The experiments were performed on a version of TwiSty dataset including tweets written by the users of six different languages: Portuguese, French, Dutch, English, German, and Italian. Logistic regression (LR), and feed-forward neural networks (FFNN) with back-propagation were used to build models in two different settings: Inter-Lingual (IL) and Cross-Lingual (CL). In the IL setting, the training and testing were performed on the same language whereas in the CL, Italian and German datasets were set aside and only used as test sets and the rest were combined to compose training and development sets. In the IL, the highest accuracy score belongs to LR whereas in the CL, FFNN with three hidden layers yields the highest score. The results show that neural network based models underperform traditional models when the size of the training set is small; however, they beat traditional models by a non-trivial margin, when they are fed with large enough data. Finally, the feature analysis confirms that men and women have different writing styles independent of their language.

Improving cluster recovery with feature rescaling factors

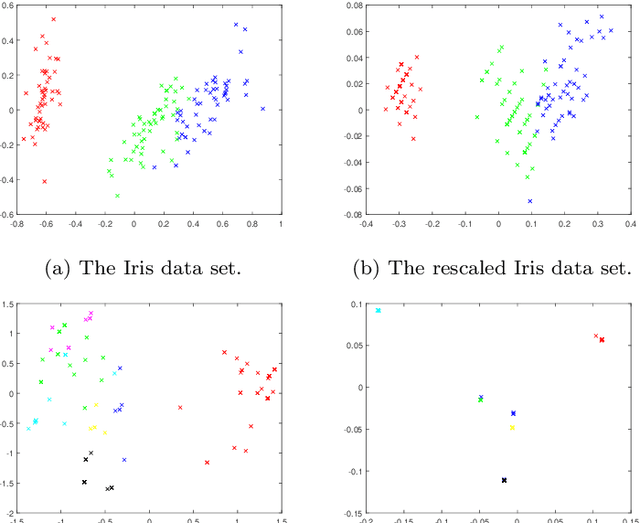
The data preprocessing stage is crucial in clustering. Features may describe entities using different scales. To rectify this, one usually applies feature normalisation aiming at rescaling features so that none of them overpowers the others in the objective function of the selected clustering algorithm. In this paper, we argue that the rescaling procedure should not treat all features identically. Instead, it should favour the features that are more meaningful for clustering. With this in mind, we introduce a feature rescaling method that takes into account the within-cluster degree of relevance of each feature. Our comprehensive simulation study, carried out on real and synthetic data, with and without noise features, clearly demonstrates that clustering methods that use the proposed data normalization strategy clearly outperform those that use traditional data normalization.

Identifying meaningful clusters in malware data

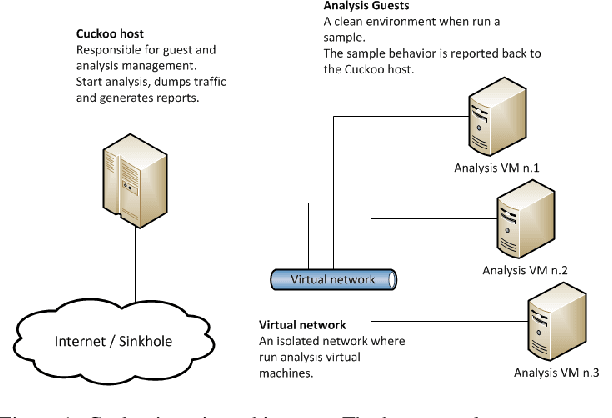
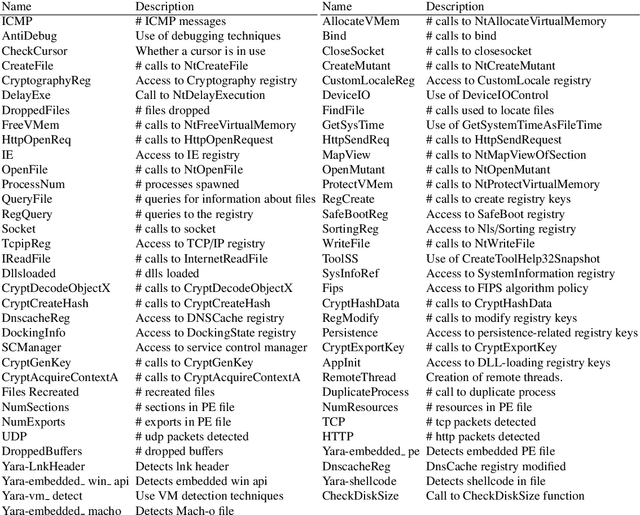
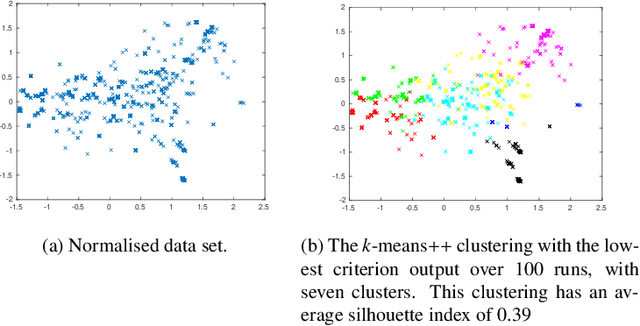
Finding meaningful clusters in drive-by-download malware data is a particularly difficult task. Malware data tends to contain overlapping clusters with wide variations of cardinality. This happens because there can be considerable similarity between malware samples (some are even said to belong to the same family), and these tend to appear in bursts. Clustering algorithms are usually applied to normalised data sets. However, the process of normalisation aims at setting features with different range values to have a similar contribution to the clustering. It does not favour more meaningful features over those that are less meaningful, an effect one should perhaps expect of the data pre-processing stage. In this paper we introduce a method to deal precisely with the problem above. This is an iterative data pre-processing method capable of aiding to increase the separation between clusters. It does so by calculating the within-cluster degree of relevance of each feature, and then it uses these as a data rescaling factor. By repeating this until convergence our malware data was separated in clear clusters, leading to a higher average silhouette width.

An efficient density-based clustering algorithm using reverse nearest neighbour

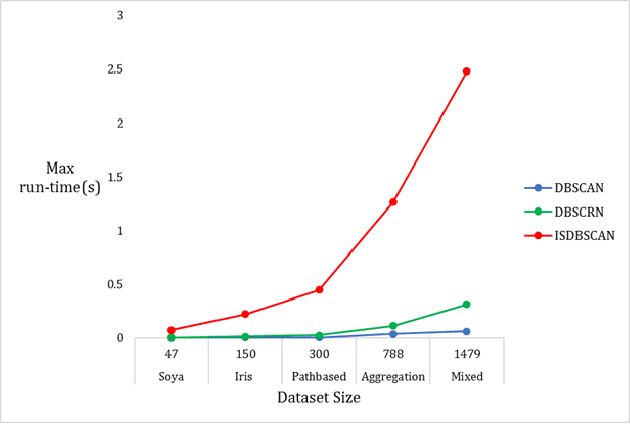
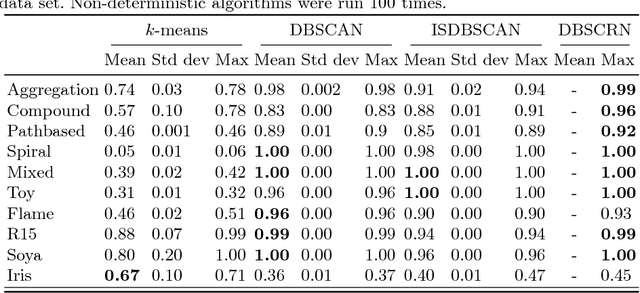
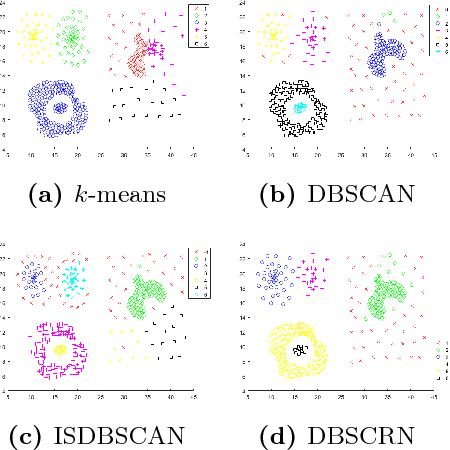
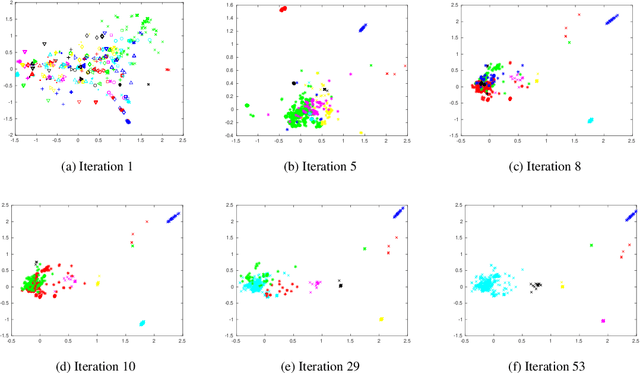
Density-based clustering is the task of discovering high-density regions of entities (clusters) that are separated from each other by contiguous regions of low-density. DBSCAN is, arguably, the most popular density-based clustering algorithm. However, its cluster recovery capabilities depend on the combination of the two parameters. In this paper we present a new density-based clustering algorithm which uses reverse nearest neighbour (RNN) and has a single parameter. We also show that it is possible to estimate a good value for this parameter using a clustering validity index. The RNN queries enable our algorithm to estimate densities taking more than a single entity into account, and to recover clusters that are not well-separated or have different densities. Our experiments on synthetic and real-world data sets show our proposed algorithm outperforms DBSCAN and its recent variant ISDBSCAN.

A-Ward_p\b{eta}: Effective hierarchical clustering using the Minkowski metric and a fast k -means initialisation

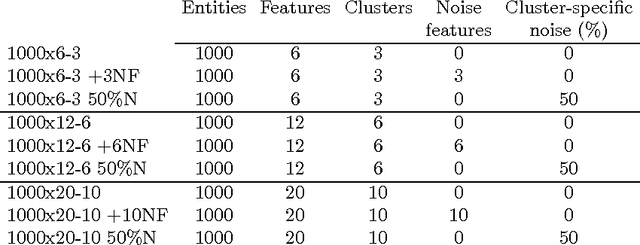
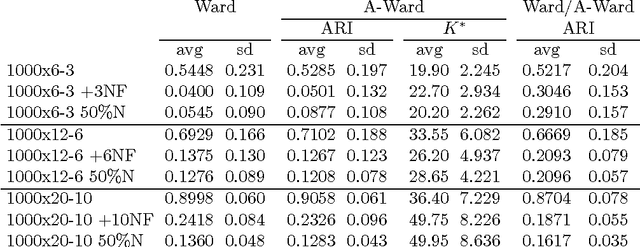
In this paper we make two novel contributions to hierarchical clustering. First, we introduce an anomalous pattern initialisation method for hierarchical clustering algorithms, called A-Ward, capable of substantially reducing the time they take to converge. This method generates an initial partition with a sufficiently large number of clusters. This allows the cluster merging process to start from this partition rather than from a trivial partition composed solely of singletons. Our second contribution is an extension of the Ward and Ward p algorithms to the situation where the feature weight exponent can differ from the exponent of the Minkowski distance. This new method, called A-Ward p\b{eta} , is able to generate a much wider variety of clustering solutions. We also demonstrate that its parameters can be estimated reasonably well by using a cluster validity index. We perform numerous experiments using data sets with two types of noise, insertion of noise features and blurring within-cluster values of some features. These experiments allow us to conclude: (i) our anomalous pattern initialisation method does indeed reduce the time a hierarchical clustering algorithm takes to complete, without negatively impacting its cluster recovery ability; (ii) A-Ward p\b{eta} provides better cluster recovery than both Ward and Ward p.

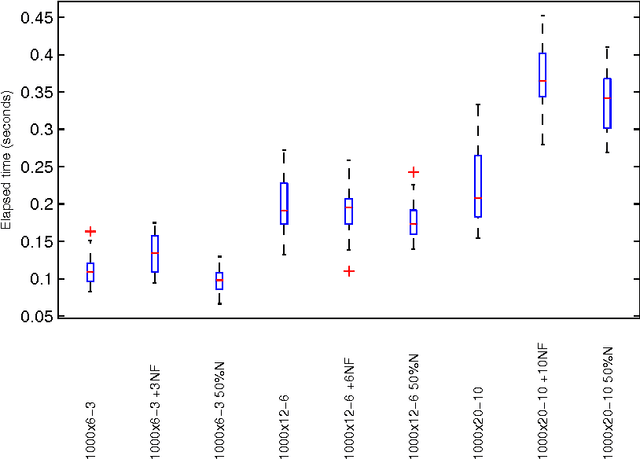
Recovering the number of clusters in data sets with noise features using feature rescaling factors

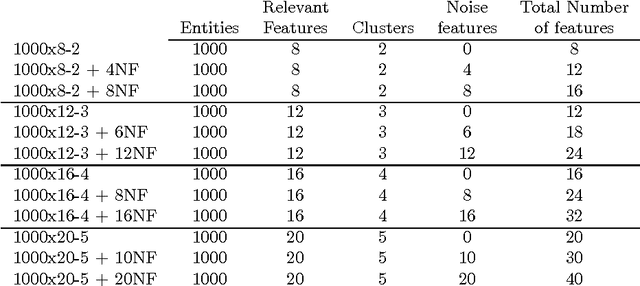
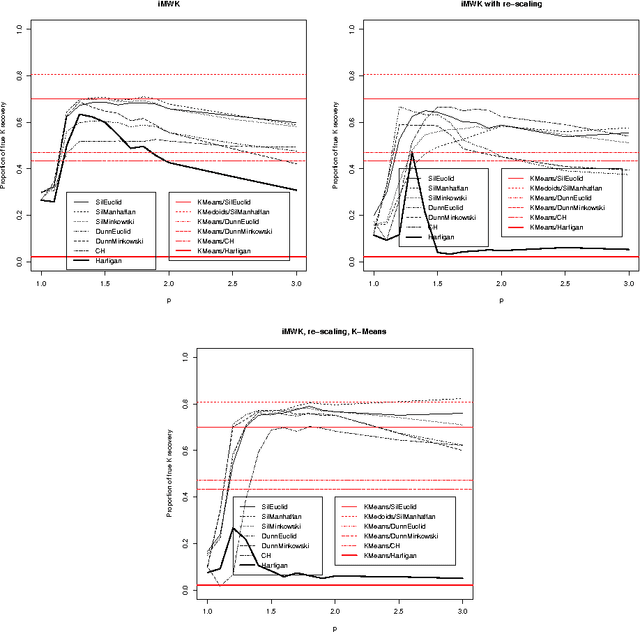
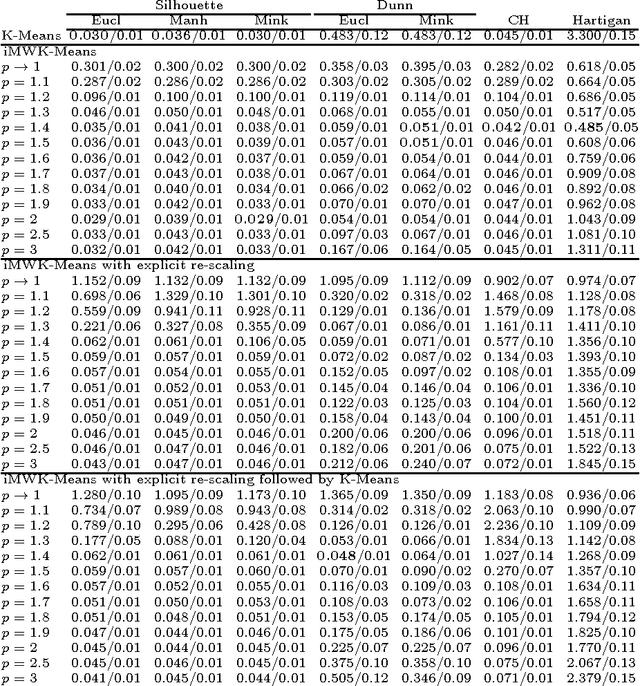
In this paper we introduce three methods for re-scaling data sets aiming at improving the likelihood of clustering validity indexes to return the true number of spherical Gaussian clusters with additional noise features. Our method obtains feature re-scaling factors taking into account the structure of a given data set and the intuitive idea that different features may have different degrees of relevance at different clusters. We experiment with the Silhouette (using squared Euclidean, Manhattan, and the p$^{th}$ power of the Minkowski distance), Dunn's, Calinski-Harabasz and Hartigan indexes on data sets with spherical Gaussian clusters with and without noise features. We conclude that our methods indeed increase the chances of estimating the true number of clusters in a data set.

A survey on feature weighting based K-Means algorithms

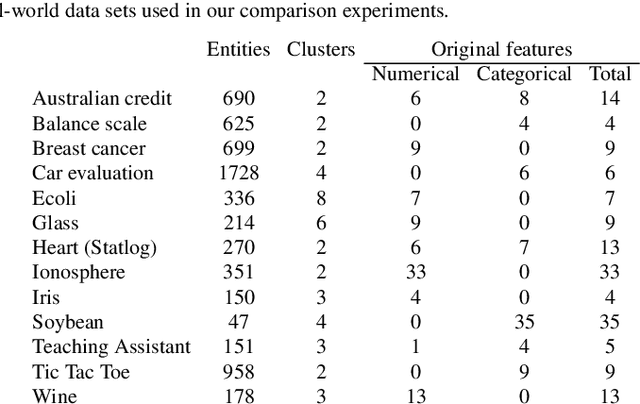
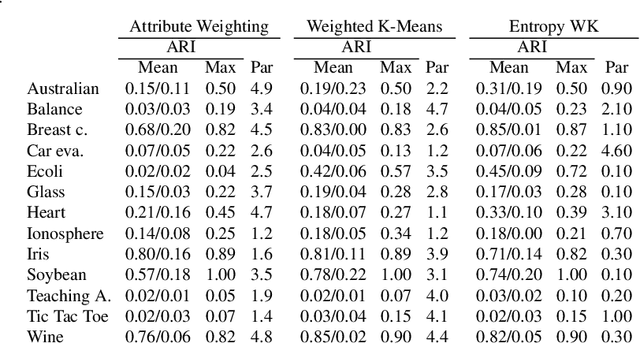
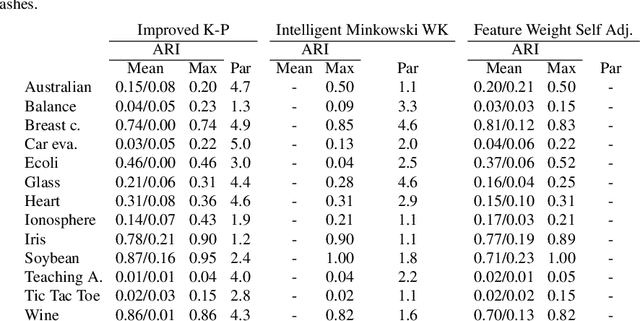
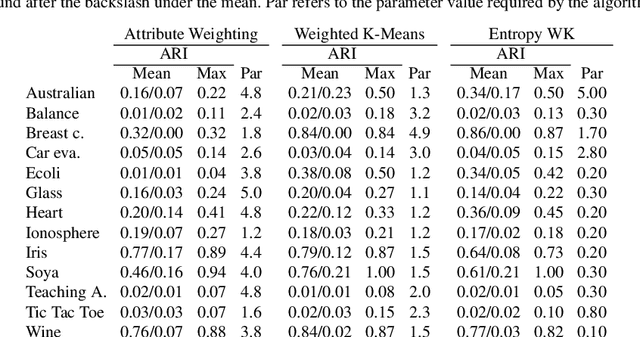
In a real-world data set there is always the possibility, rather high in our opinion, that different features may have different degrees of relevance. Most machine learning algorithms deal with this fact by either selecting or deselecting features in the data preprocessing phase. However, we maintain that even among relevant features there may be different degrees of relevance, and this should be taken into account during the clustering process. With over 50 years of history, K-Means is arguably the most popular partitional clustering algorithm there is. The first K-Means based clustering algorithm to compute feature weights was designed just over 30 years ago. Various such algorithms have been designed since but there has not been, to our knowledge, a survey integrating empirical evidence of cluster recovery ability, common flaws, and possible directions for future research. This paper elaborates on the concept of feature weighting and addresses these issues by critically analysing some of the most popular, or innovative, feature weighting mechanisms based in K-Means.