Nonparametric consistency for maximum likelihood estimation and clustering based on mixtures of elliptically-symmetric distributions

The consistency of the maximum likelihood estimator for mixtures of elliptically-symmetric distributions for estimating its population version is shown, where the underlying distribution $P$ is nonparametric and does not necessarily belong to the class of mixtures on which the estimator is based. In a situation where $P$ is a mixture of well enough separated but nonparametric distributions it is shown that the components of the population version of the estimator correspond to the well separated components of $P$. This provides some theoretical justification for the use of such estimators for cluster analysis in case that $P$ has well separated subpopulations even if these subpopulations differ from what the mixture model assumes.

Some issues in robust clustering

Some key issues in robust clustering are discussed with focus on Gaussian mixture model based clustering, namely the formal definition of outliers, ambiguity between groups of outliers and clusters, the interaction between robust clustering and the estimation of the number of clusters, the essential dependence of (not only) robust clustering on tuning decisions, and shortcomings of existing measurements of cluster stability when it comes to outliers.

Characterization and Development of Average Silhouette Width Clustering

The purpose of this paper is to introduced a new clustering methodology. This paper is divided into three parts. In the first part we have developed the axiomatic theory for the average silhouette width (ASW) index. There are different ways to investigate the quality and characteristics of clustering methods such as validation indices using simulations and real data experiments, model-based theory, and non-model-based theory known as the axiomatic theory. In this work we have not only taken the empirical approach of validation of clustering results through simulations, but also focus on the development of the axiomatic theory. In the second part we have presented a novel clustering methodology based on the optimization of the ASW index. We have considered the problem of estimation of number of clusters and finding clustering against this number simultaneously. Two algorithms are proposed. The proposed algorithms are evaluated against several partitioning and hierarchical clustering methods. An intensive empirical comparison of the different distance metrics on the various clustering methods is conducted. In the third part we have considered two application domains\textemdash novel single cell RNA sequencing datasets and rainfall data to cluster weather stations.

Clustering by Optimizing the Average Silhouette Width

In this paper, we propose a unified clustering approach that can estimate number of clusters and produce clustering against this number simultaneously. Average silhouette width (ASW) is a widely used standard cluster quality index. We define a distance based objective function that optimizes ASW for clustering. The proposed algorithm named as OSil, only, needs data observations as an input without any prior knowledge of the number of clusters. This work is about thorough investigation of the proposed methodology, its usefulness and limitations. A vast spectrum of clustering structures were generated, and several well-known clustering methods including partitioning, hierarchical, density based, and spatial methods were consider as the competitor of the proposed methodology. Simulation reveals that OSil algorithm has shown superior perform in terms of clustering quality than all clustering methods included in the study. OSil can find well separated, compact clusters and have shown better performance for the estimation of number of clusters than several methods. Apart from the proposal of the new methodology and it's investigation this papers offer a systematic analysis on the estimation of cluster indices, some of which never appeared together in comparative simulation setup before. The study offers many insightful findings useful for the selection of the clustering methods and indices.

Distance for Functional Data Clustering Based on Smoothing Parameter Commutation

We propose a novel method to determine the dissimilarity between subjects for functional data clustering. Spline smoothing or interpolation is common to deal with data of such type. Instead of estimating the best-representing curve for each subject as fixed during clustering, we measure the dissimilarity between subjects based on varying curve estimates with commutation of smoothing parameters pair-by-pair (of subjects). The intuitions are that smoothing parameters of smoothing splines reflect inverse signal-to-noise ratios and that applying an identical smoothing parameter the smoothed curves for two similar subjects are expected to be close. The effectiveness of our proposal is shown through simulations comparing to other dissimilarity measures. It also has several pragmatic advantages. First, missing values or irregular time points can be handled directly, thanks to the nature of smoothing splines. Second, conventional clustering method based on dissimilarity can be employed straightforward, and the dissimilarity also serves as a useful tool for outlier detection. Third, the implementation is almost handy since subroutines for smoothing splines and numerical integration are widely available. Fourth, the computational complexity does not increase and is parallel with that in calculating Euclidean distance between curves estimated by smoothing splines.

Recovering the number of clusters in data sets with noise features using feature rescaling factors

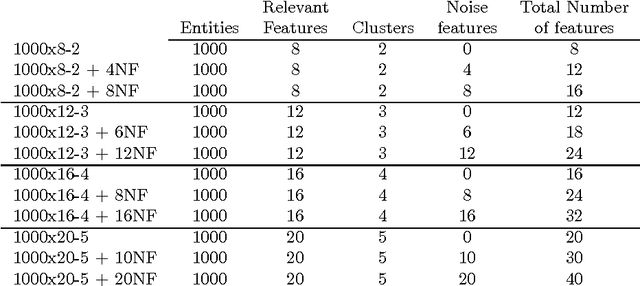
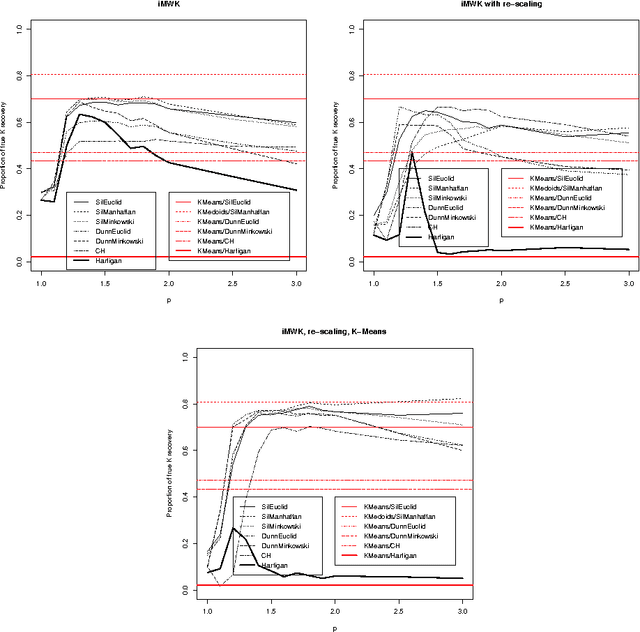
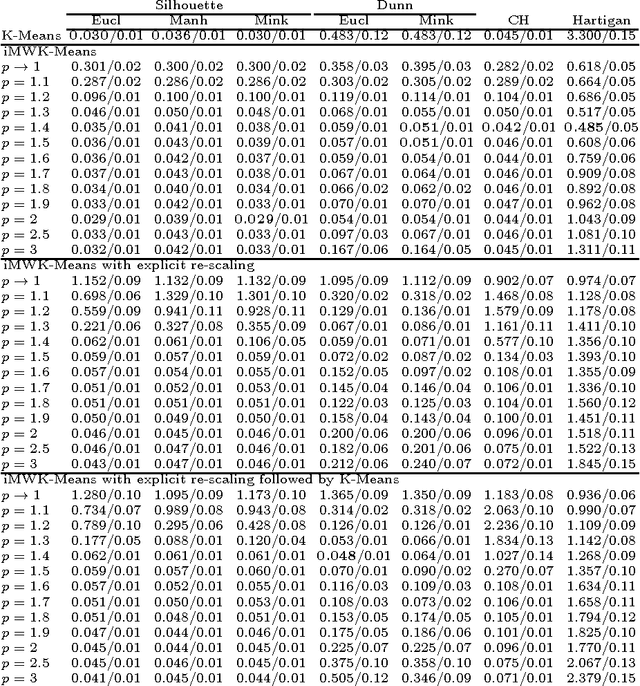
In this paper we introduce three methods for re-scaling data sets aiming at improving the likelihood of clustering validity indexes to return the true number of spherical Gaussian clusters with additional noise features. Our method obtains feature re-scaling factors taking into account the structure of a given data set and the intuitive idea that different features may have different degrees of relevance at different clusters. We experiment with the Silhouette (using squared Euclidean, Manhattan, and the p$^{th}$ power of the Minkowski distance), Dunn's, Calinski-Harabasz and Hartigan indexes on data sets with spherical Gaussian clusters with and without noise features. We conclude that our methods indeed increase the chances of estimating the true number of clusters in a data set.