Deep Gaussian Process-based Cost-Aware Batch Bayesian Optimization for Complex Materials Design Campaigns

The accelerating pace and expanding scope of materials discovery demand optimization frameworks that efficiently navigate vast, nonlinear design spaces while judiciously allocating limited evaluation resources. We present a cost-aware, batch Bayesian optimization scheme powered by deep Gaussian process (DGP) surrogates and a heterotopic querying strategy. Our DGP surrogate, formed by stacking GP layers, models complex hierarchical relationships among high-dimensional compositional features and captures correlations across multiple target properties, propagating uncertainty through successive layers. We integrate evaluation cost into an upper-confidence-bound acquisition extension, which, together with heterotopic querying, proposes small batches of candidates in parallel, balancing exploration of under-characterized regions with exploitation of high-mean, low-variance predictions across correlated properties. Applied to refractory high-entropy alloys for high-temperature applications, our framework converges to optimal formulations in fewer iterations with cost-aware queries than conventional GP-based BO, highlighting the value of deep, uncertainty-aware, cost-sensitive strategies in materials campaigns.

Data Driven Insights into Composition Property Relationships in FCC High Entropy Alloys

Structural High Entropy Alloys (HEAs) are crucial in advancing technology across various sectors, including aerospace, automotive, and defense industries. However, the scarcity of integrated chemistry, process, structure, and property data presents significant challenges for predictive property modeling. Given the vast design space of these alloys, uncovering the underlying patterns is essential yet difficult, requiring advanced methods capable of learning from limited and heterogeneous datasets. This work presents several sensitivity analyses, highlighting key elemental contributions to mechanical behavior, including insights into the compositional factors associated with brittle and fractured responses observed during nanoindentation testing in the BIRDSHOT center NiCoFeCrVMnCuAl system dataset. Several encoder decoder based chemistry property models, carefully tuned through Bayesian multi objective hyperparameter optimization, are evaluated for mapping alloy composition to six mechanical properties. The models achieve competitive or superior performance to conventional regressors across all properties, particularly for yield strength and the UTS/YS ratio, demonstrating their effectiveness in capturing complex composition property relationships.

Physics-Informed Gaussian Process Classification for Constraint-Aware Alloy Design

Alloy design can be framed as a constraint-satisfaction problem. Building on previous methodologies, we propose equipping Gaussian Process Classifiers (GPCs) with physics-informed prior mean functions to model the boundaries of feasible design spaces. Through three case studies, we highlight the utility of informative priors for handling constraints on continuous and categorical properties. (1) Phase Stability: By incorporating CALPHAD predictions as priors for solid-solution phase stability, we enhance model validation using a publicly available XRD dataset. (2) Phase Stability Prediction Refinement: We demonstrate an in silico active learning approach to efficiently correct phase diagrams. (3) Continuous Property Thresholds: By embedding priors into continuous property models, we accelerate the discovery of alloys meeting specific property thresholds via active learning. In each case, integrating physics-based insights into the classification framework substantially improved model performance, demonstrating an efficient strategy for constraint-aware alloy design.

Towards Autonomous Experimentation: Bayesian Optimization over Problem Formulation Space for Accelerated Alloy Development

Accelerated discovery in materials science demands autonomous systems capable of dynamically formulating and solving design problems. In this work, we introduce a novel framework that leverages Bayesian optimization over a problem formulation space to identify optimal design formulations in line with decision-maker preferences. By mapping various design scenarios to a multi attribute utility function, our approach enables the system to balance conflicting objectives such as ductility, yield strength, density, and solidification range without requiring an exact problem definition at the outset. We demonstrate the efficacy of our method through an in silico case study on a Mo-Nb-Ti-V-W alloy system targeted for gas turbine engine blade applications. The framework converges on a sweet spot that satisfies critical performance thresholds, illustrating that integrating problem formulation discovery into the autonomous design loop can significantly streamline the experimental process. Future work will incorporate human feedback to further enhance the adaptability of the system in real-world experimental settings.

Label Propagation Training Schemes for Physics-Informed Neural Networks and Gaussian Processes

This paper proposes a semi-supervised methodology for training physics-informed machine learning methods. This includes self-training of physics-informed neural networks and physics-informed Gaussian processes in isolation, and the integration of the two via co-training. We demonstrate via extensive numerical experiments how these methods can ameliorate the issue of propagating information forward in time, which is a common failure mode of physics-informed machine learning.

Efficient Propagation of Uncertainty via Reordering Monte Carlo Samples

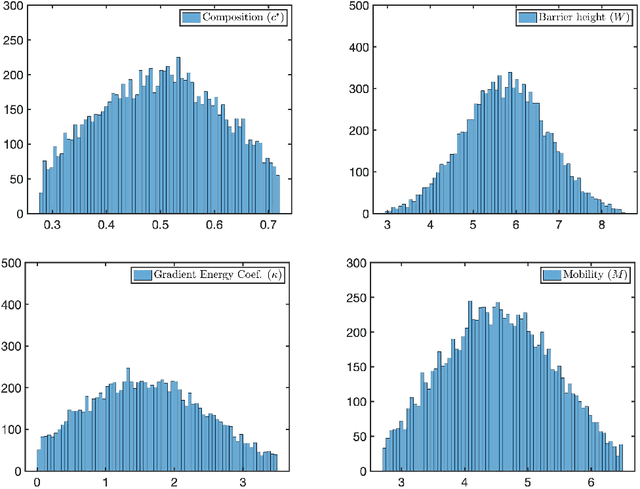
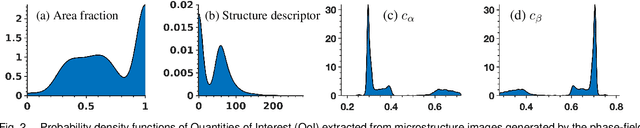
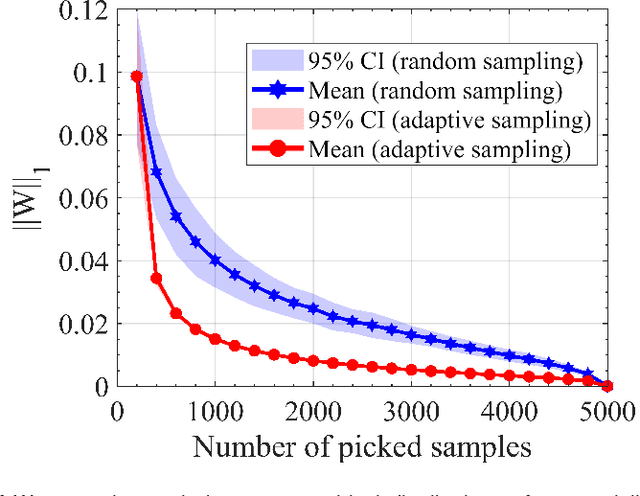
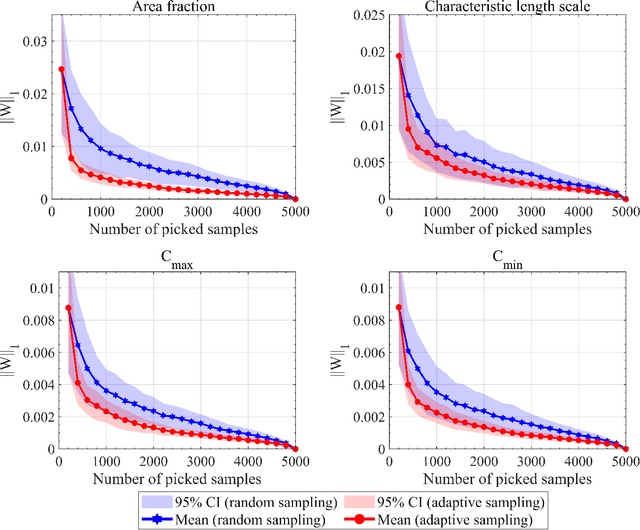
Uncertainty analysis in the outcomes of model predictions is a key element in decision-based material design to establish confidence in the models and evaluate the fidelity of models. Uncertainty Propagation (UP) is a technique to determine model output uncertainties based on the uncertainty in its input variables. The most common and simplest approach to propagate the uncertainty from a model inputs to its outputs is by feeding a large number of samples to the model, known as Monte Carlo (MC) simulation which requires exhaustive sampling from the input variable distributions. However, MC simulations are impractical when models are computationally expensive. In this work, we investigate the hypothesis that while all samples are useful on average, some samples must be more useful than others. Thus, reordering MC samples and propagating more useful samples can lead to enhanced convergence in statistics of interest earlier and thus, reducing the computational burden of UP process. Here, we introduce a methodology to adaptively reorder MC samples and show how it results in reduction of computational expense of UP processes.

Deep Multimodal Transfer-Learned Regression in Data-Poor Domains

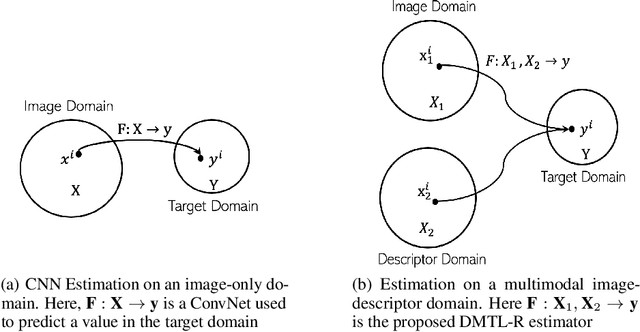
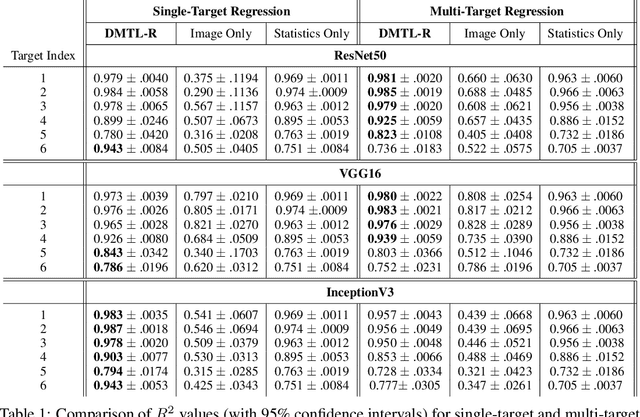
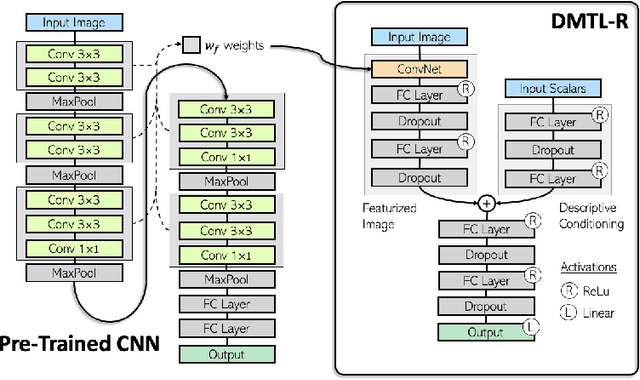
In many real-world applications of deep learning, estimation of a target may rely on various types of input data modes, such as audio-video, image-text, etc. This task can be further complicated by a lack of sufficient data. Here we propose a Deep Multimodal Transfer-Learned Regressor (DMTL-R) for multimodal learning of image and feature data in a deep regression architecture effective at predicting target parameters in data-poor domains. Our model is capable of fine-tuning a given set of pre-trained CNN weights on a small amount of training image data, while simultaneously conditioning on feature information from a complimentary data mode during network training, yielding more accurate single-target or multi-target regression than can be achieved using the images or the features alone. We present results using phase-field simulation microstructure images with an accompanying set of physical features, using pre-trained weights from various well-known CNN architectures, which demonstrate the efficacy of the proposed multimodal approach.

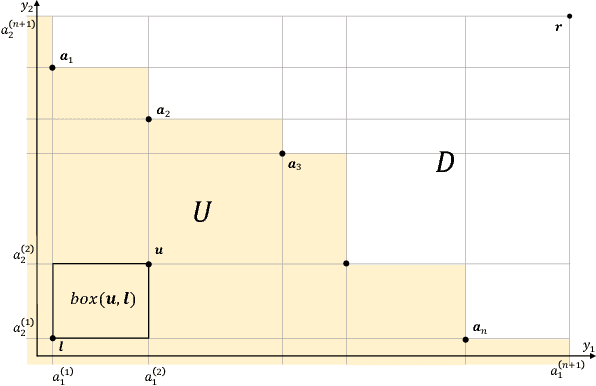
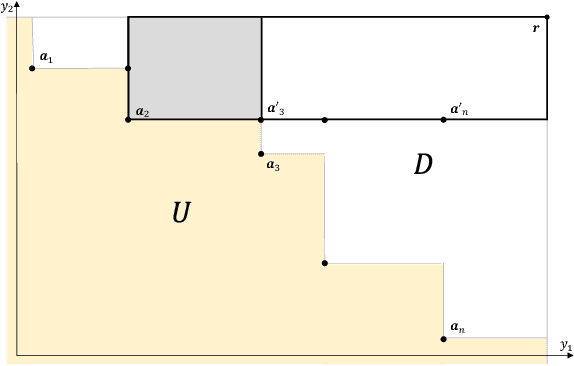
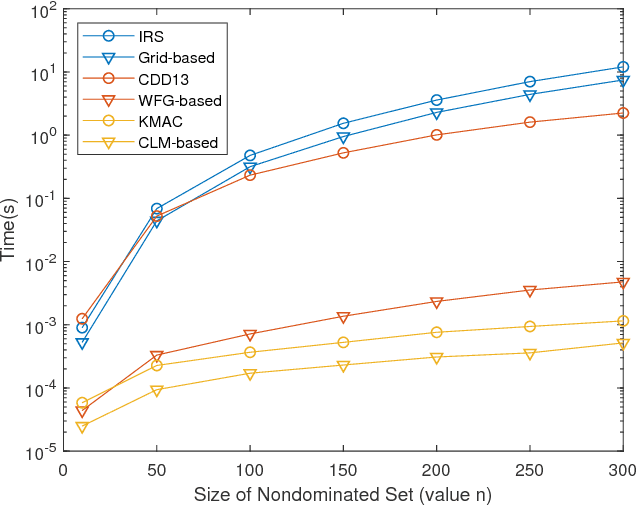
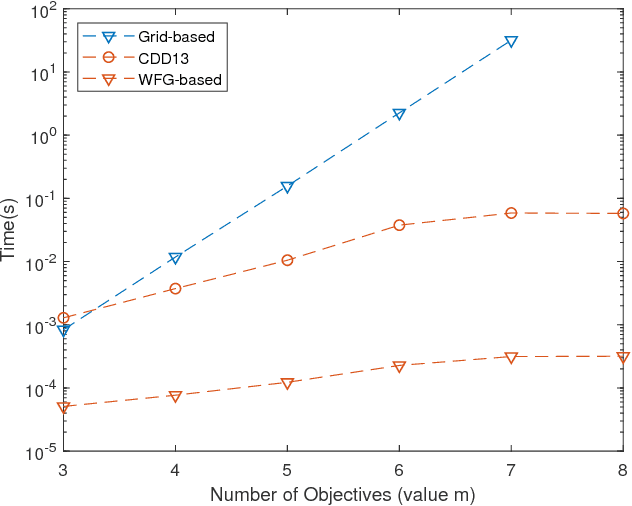
Fast Exact Computation of Expected HyperVolume Improvement

In multi-objective Bayesian optimization and surrogate-based evolutionary algorithms, Expected HyperVolume Improvement (EHVI) is widely used as the acquisition function to guide the search approaching the Pareto front. This paper focuses on the exact calculation of EHVI given a nondominated set, for which the existing exact algorithms are complex and can be inefficient for problems with more than three objectives. Integrating with different decomposition algorithms, we propose a new method for calculating the integral in each decomposed high-dimensional box in constant time. We develop three new exact EHVI calculation algorithms based on three region decomposition methods. The first grid-based algorithm has a complexity of $O(m\cdot n^m)$ with $n$ denoting the size of the nondominated set and $m$ the number of objectives. The Walking Fish Group (WFG)-based algorithm has a worst-case complexity of $O(m\cdot 2^n)$ but has a better average performance. These two can be applied for problems with any $m$. The third CLM-based algorithm is only for $m=3$ and asymptotically optimal with complexity $\Theta(n\log{n})$. Performance comparison results show that all our three algorithms are at least twice faster than the state-of-the-art algorithms with the same decomposition methods. When $m>3$, our WFG-based algorithm can be over $10^2$ faster than the corresponding existing algorithms. Our algorithm is demonstrated in an example involving efficient multi-objective material design with Bayesian optimization.