Towards Autonomous Experimentation: Bayesian Optimization over Problem Formulation Space for Accelerated Alloy Development

Accelerated discovery in materials science demands autonomous systems capable of dynamically formulating and solving design problems. In this work, we introduce a novel framework that leverages Bayesian optimization over a problem formulation space to identify optimal design formulations in line with decision-maker preferences. By mapping various design scenarios to a multi attribute utility function, our approach enables the system to balance conflicting objectives such as ductility, yield strength, density, and solidification range without requiring an exact problem definition at the outset. We demonstrate the efficacy of our method through an in silico case study on a Mo-Nb-Ti-V-W alloy system targeted for gas turbine engine blade applications. The framework converges on a sweet spot that satisfies critical performance thresholds, illustrating that integrating problem formulation discovery into the autonomous design loop can significantly streamline the experimental process. Future work will incorporate human feedback to further enhance the adaptability of the system in real-world experimental settings.

Supply Risk-Aware Alloy Discovery and Design

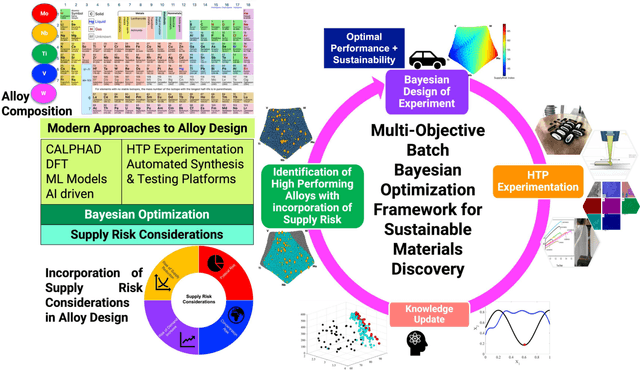
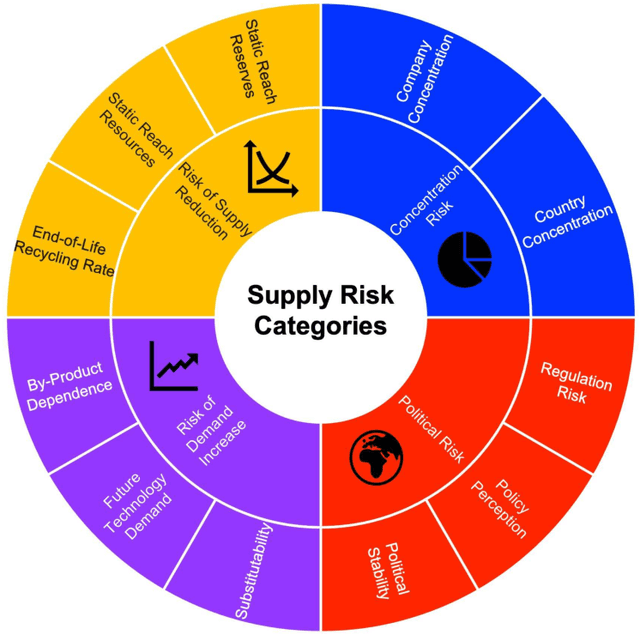
Materials design is a critical driver of innovation, yet overlooking the technological, economic, and environmental risks inherent in materials and their supply chains can lead to unsustainable and risk-prone solutions. To address this, we present a novel risk-aware design approach that integrates Supply-Chain Aware Design Strategies into the materials development process. This approach leverages existing language models and text analysis to develop a specialized model for predicting materials feedstock supply risk indices. To efficiently navigate the multi-objective, multi-constraint design space, we employ Batch Bayesian Optimization (BBO), enabling the identification of Pareto-optimal high entropy alloys (HEAs) that balance performance objectives with minimized supply risk. A case study using the MoNbTiVW system demonstrates the efficacy of our approach in four scenarios, highlighting the significant impact of incorporating supply risk into the design process. By optimizing for both performance and supply risk, we ensure that the developed alloys are not only high-performing but also sustainable and economically viable. This integrated approach represents a critical step towards a future where materials discovery and design seamlessly consider sustainability, supply chain dynamics, and comprehensive life cycle analysis.

Efficient Propagation of Uncertainty via Reordering Monte Carlo Samples

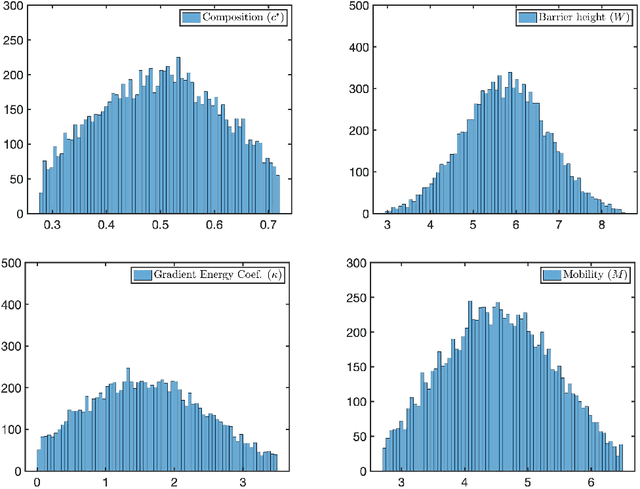
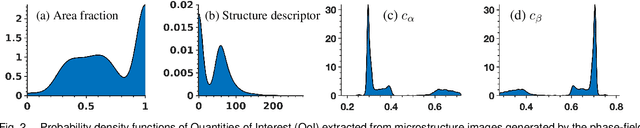
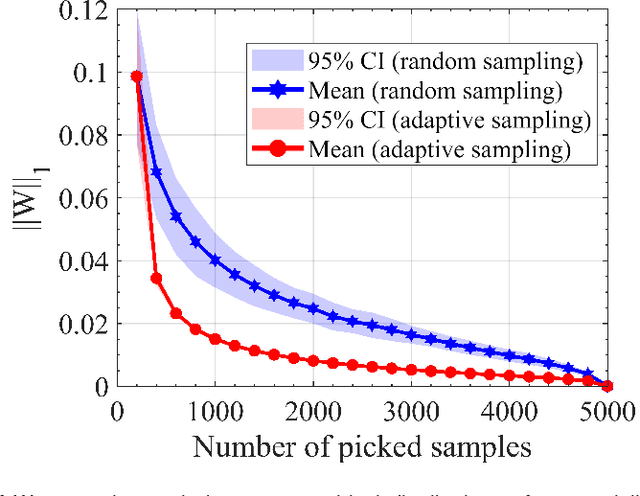
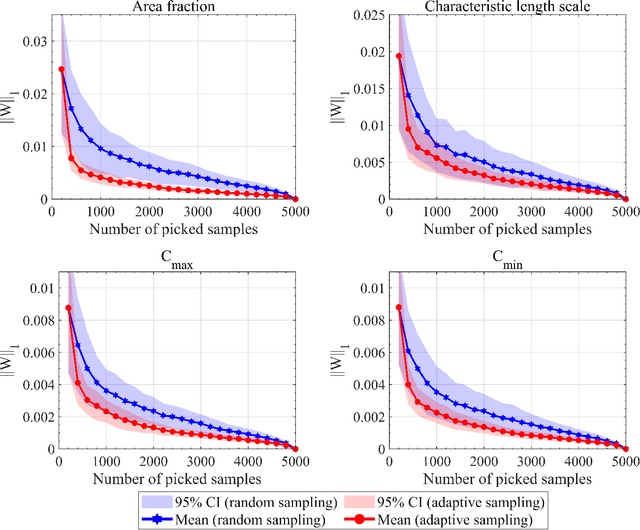
Uncertainty analysis in the outcomes of model predictions is a key element in decision-based material design to establish confidence in the models and evaluate the fidelity of models. Uncertainty Propagation (UP) is a technique to determine model output uncertainties based on the uncertainty in its input variables. The most common and simplest approach to propagate the uncertainty from a model inputs to its outputs is by feeding a large number of samples to the model, known as Monte Carlo (MC) simulation which requires exhaustive sampling from the input variable distributions. However, MC simulations are impractical when models are computationally expensive. In this work, we investigate the hypothesis that while all samples are useful on average, some samples must be more useful than others. Thus, reordering MC samples and propagating more useful samples can lead to enhanced convergence in statistics of interest earlier and thus, reducing the computational burden of UP process. Here, we introduce a methodology to adaptively reorder MC samples and show how it results in reduction of computational expense of UP processes.