Self-Adaptive Physics-Informed Neural Networks using a Soft Attention Mechanism

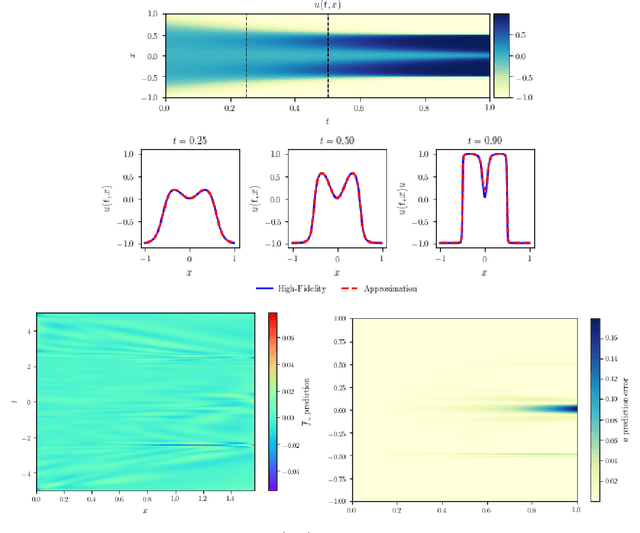
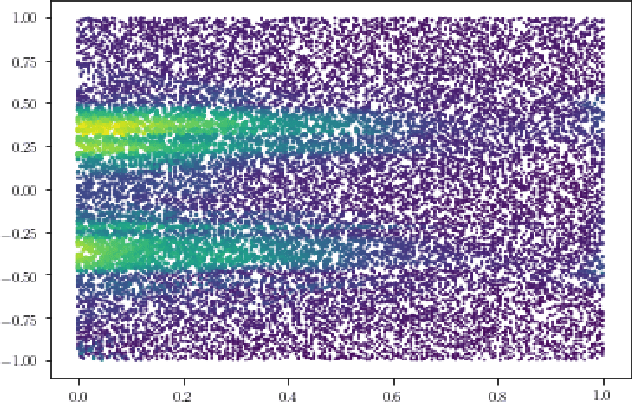
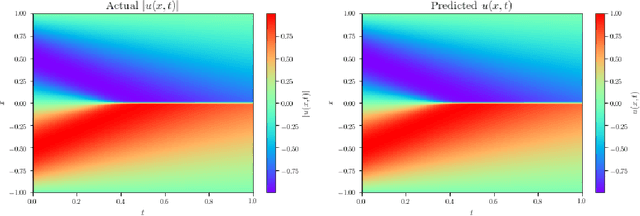
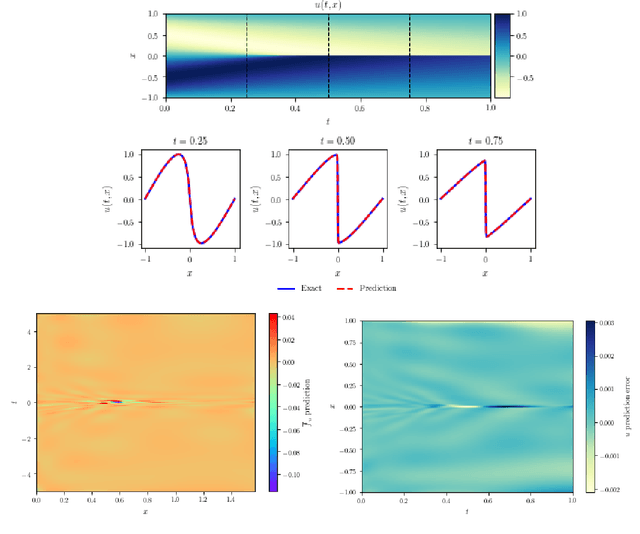
Physics-Informed Neural Networks (PINNs) have emerged recently as a promising application of deep neural networks to the numerical solution of nonlinear partial differential equations (PDEs). However, the original PINN algorithm is known to suffer from stability and accuracy problems in cases where the solution has sharp spatio-temporal transitions. These stiff PDEs require an unreasonably large number of collocation points to be solved accurately. It has been recognized that adaptive procedures are needed to force the neural network to fit accurately the stubborn spots in the solution of stiff PDEs. To accomplish this, previous approaches have used fixed weights hard-coded over regions of the solution deemed to be important. In this paper, we propose a fundamentally new method to train PINNs adaptively, where the adaptation weights are fully trainable, so the neural network learns by itself which regions of the solution are difficult and is forced to focus on them, which is reminiscent of soft multiplicative-mask attention mechanism used in computer vision. The basic idea behind these Self-Adaptive PINNs is to make the weights increase where the corresponding loss is higher, which is accomplished by training the network to simultaneously minimize the losses and maximize the weights, i.e., to find a saddle point in the cost surface. We show that this is formally equivalent to solving a PDE-constrained optimization problem using a penalty-based method, though in a way where the monotonically-nondecreasing penalty coefficients are trainable. Numerical experiments with an Allen-Cahn stiff PDE, the Self-Adaptive PINN outperformed other state-of-the-art PINN algorithms in L2 error by a wide margin, while using a smaller number of training epochs. An Appendix contains additional results with Burger's and Helmholtz PDEs, which confirmed the trends observed in the Allen-Cahn experiments.

Deep Multimodal Transfer-Learned Regression in Data-Poor Domains

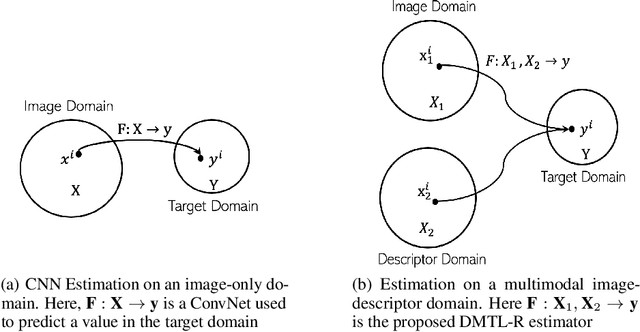
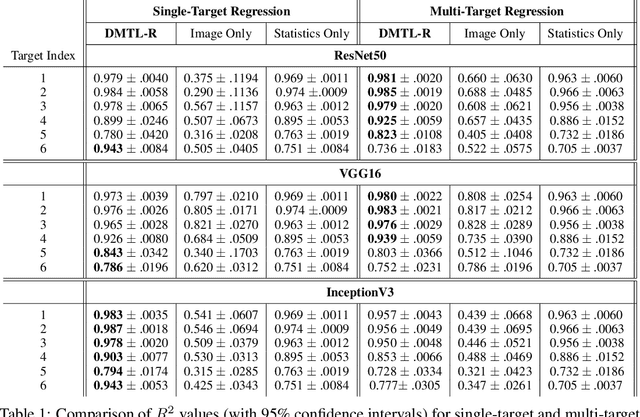
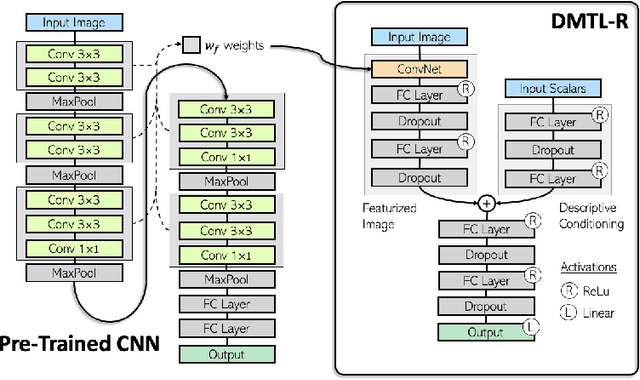
In many real-world applications of deep learning, estimation of a target may rely on various types of input data modes, such as audio-video, image-text, etc. This task can be further complicated by a lack of sufficient data. Here we propose a Deep Multimodal Transfer-Learned Regressor (DMTL-R) for multimodal learning of image and feature data in a deep regression architecture effective at predicting target parameters in data-poor domains. Our model is capable of fine-tuning a given set of pre-trained CNN weights on a small amount of training image data, while simultaneously conditioning on feature information from a complimentary data mode during network training, yielding more accurate single-target or multi-target regression than can be achieved using the images or the features alone. We present results using phase-field simulation microstructure images with an accompanying set of physical features, using pre-trained weights from various well-known CNN architectures, which demonstrate the efficacy of the proposed multimodal approach.