Self-Adaptive Physics-Informed Neural Networks using a Soft Attention Mechanism
Paper and Code
Sep 15, 2020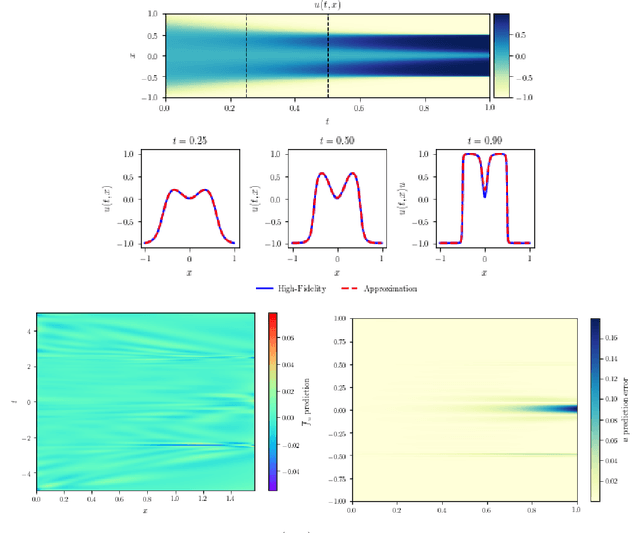
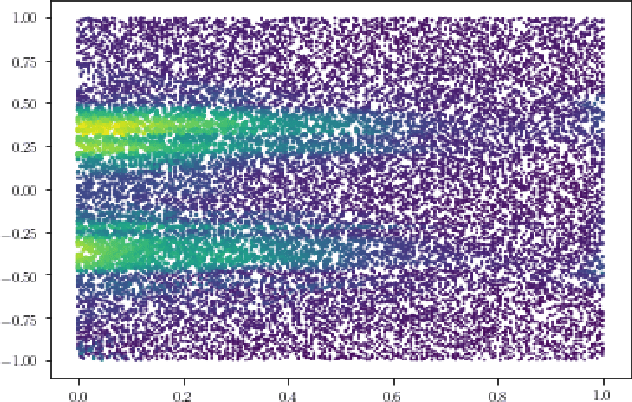
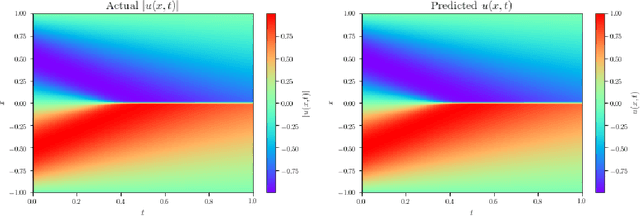
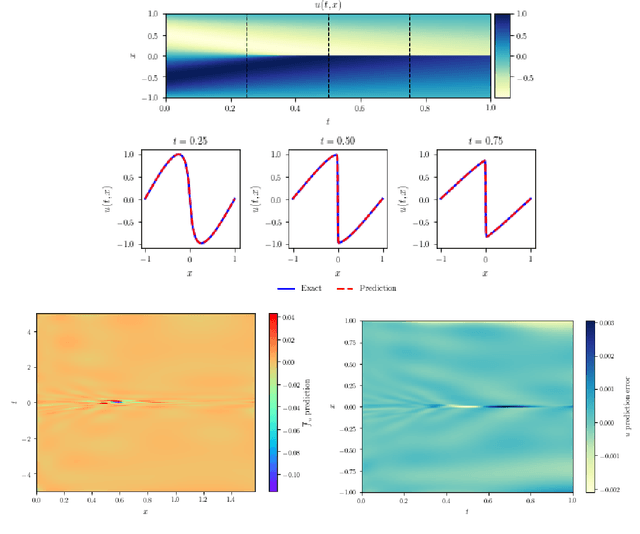
Physics-Informed Neural Networks (PINNs) have emerged recently as a promising application of deep neural networks to the numerical solution of nonlinear partial differential equations (PDEs). However, the original PINN algorithm is known to suffer from stability and accuracy problems in cases where the solution has sharp spatio-temporal transitions. These stiff PDEs require an unreasonably large number of collocation points to be solved accurately. It has been recognized that adaptive procedures are needed to force the neural network to fit accurately the stubborn spots in the solution of stiff PDEs. To accomplish this, previous approaches have used fixed weights hard-coded over regions of the solution deemed to be important. In this paper, we propose a fundamentally new method to train PINNs adaptively, where the adaptation weights are fully trainable, so the neural network learns by itself which regions of the solution are difficult and is forced to focus on them, which is reminiscent of soft multiplicative-mask attention mechanism used in computer vision. The basic idea behind these Self-Adaptive PINNs is to make the weights increase where the corresponding loss is higher, which is accomplished by training the network to simultaneously minimize the losses and maximize the weights, i.e., to find a saddle point in the cost surface. We show that this is formally equivalent to solving a PDE-constrained optimization problem using a penalty-based method, though in a way where the monotonically-nondecreasing penalty coefficients are trainable. Numerical experiments with an Allen-Cahn stiff PDE, the Self-Adaptive PINN outperformed other state-of-the-art PINN algorithms in L2 error by a wide margin, while using a smaller number of training epochs. An Appendix contains additional results with Burger's and Helmholtz PDEs, which confirmed the trends observed in the Allen-Cahn experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge