At-Scale Sparse Deep Neural Network Inference with Efficient GPU Implementation

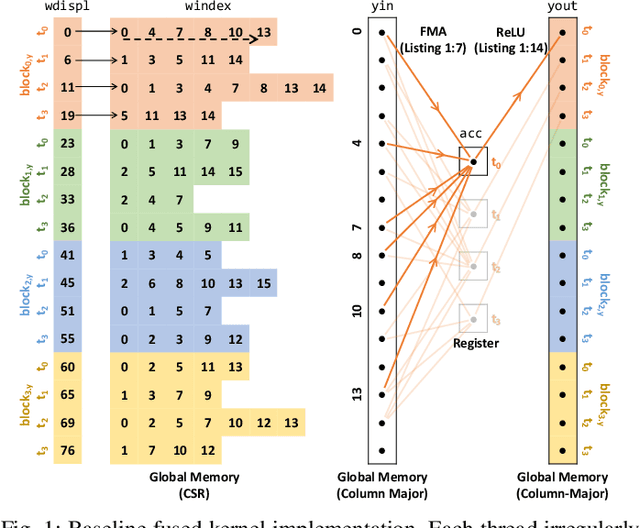
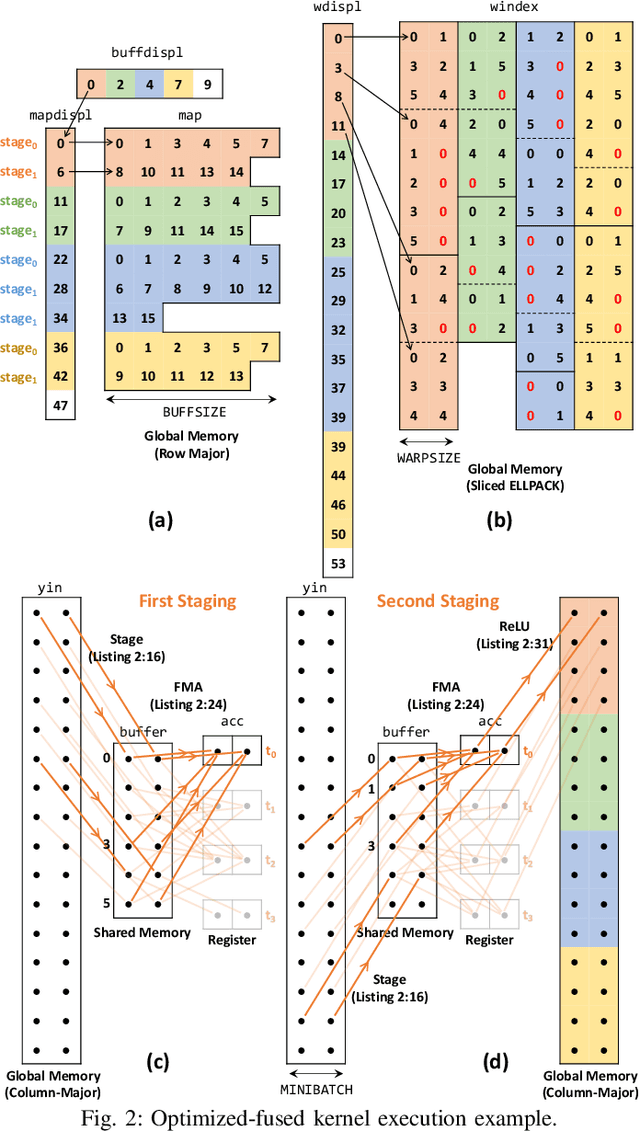
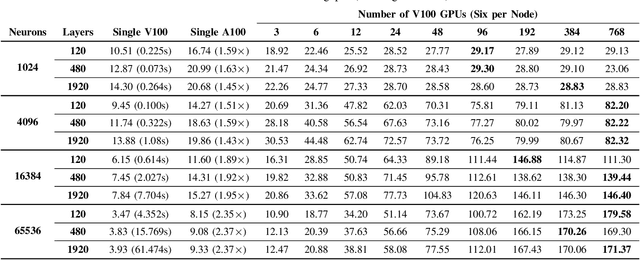
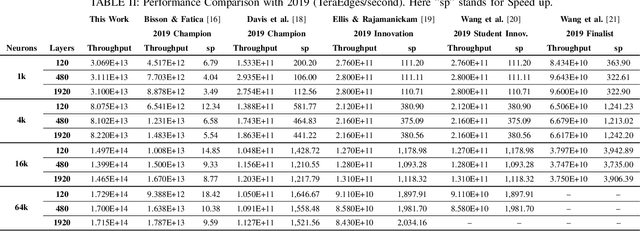
This paper presents GPU performance optimization and scaling results for inference models of the Sparse Deep Neural Network Challenge 2020. Demands for network quality have increased rapidly, pushing the size and thus the memory requirements of many neural networks beyond the capacity of available accelerators. Sparse deep neural networks (SpDNN) have shown promise for reining in the memory footprint of large neural networks. However, there is room for improvement in implementing SpDNN operations on GPUs. This work presents optimized sparse matrix multiplication kernels fused with the ReLU function. The optimized kernels reuse input feature maps from the shared memory and sparse weights from registers. For multi-GPU parallelism, our SpDNN implementation duplicates weights and statically partition the feature maps across GPUs. Results for the challenge benchmarks show that the proposed kernel design and multi-GPU parallelization achieve up to 180 tera-edges per second inference throughput. These results are up to 4.3x faster for a single GPU and an order of magnitude faster at full scale than those of the champion of the 2019 Sparse Deep Neural Network Graph Challenge for the same generation of NVIDIA V100 GPUs. Using the same implementation, we also show single-GPU throughput on NVIDIA A100 is 2.37$\times$ faster than V100.

Risk-Averse Explore-Then-Commit Algorithms for Finite-Time Bandits

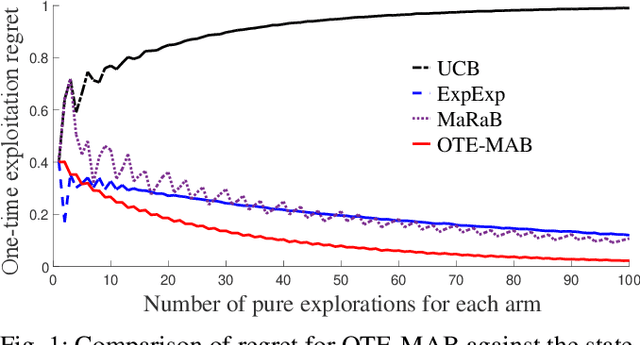
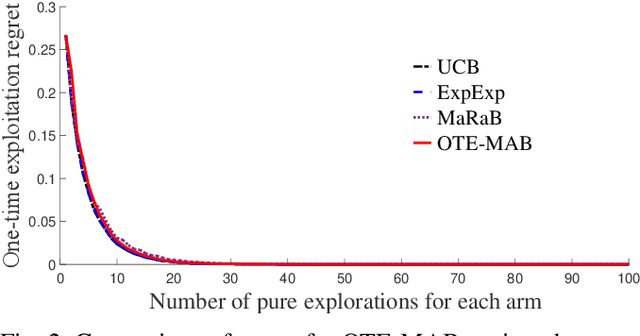
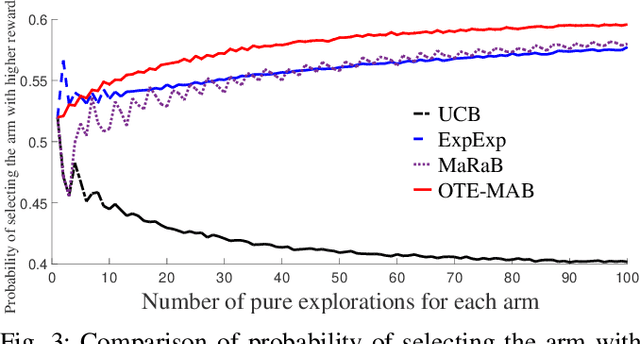
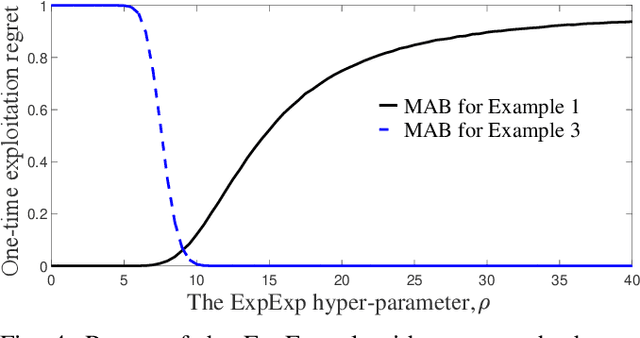
In this paper, we study multi-armed bandit problems in explore-then-commit setting. In our proposed explore-then-commit setting, the goal is to identify the best arm after a pure experimentation (exploration) phase and exploit it once or for a given finite number of times. We identify that although the arm with the highest expected reward is the most desirable objective for infinite exploitations, it is not necessarily the one that is most probable to have the highest reward in a single or finite-time exploitations. Alternatively, we advocate the idea of risk-aversion where the objective is to compete against the arm with the best risk-return trade-off. Then, we propose two algorithms whose objectives are to select the arm that is most probable to reward the most. Using a new notion of finite-time exploitation regret, we find an upper bound for the minimum number of experiments before commitment, to guarantee an upper bound for the regret. As compared to existing risk-averse bandit algorithms, our algorithms do not rely on hyper-parameters, resulting in a more robust behavior in practice, which is verified by the numerical evaluation.