Developing Hybrid Machine Learning Models to Assign Health Score to Railcar Fleets for Optimal Decision Making

A large amount of data is generated during the operation of a railcar fleet, which can easily lead to dimensional disaster and reduce the resiliency of the railcar network. To solve these issues and offer predictive maintenance, this research introduces a hybrid fault diagnosis expert system method that combines density-based spatial clustering of applications with noise (DBSCAN) and principal component analysis (PCA). Firstly, the DBSCAN method is used to cluster categorical data that are similar to one another within the same group. Secondly, PCA algorithm is applied to reduce the dimensionality of the data and eliminate redundancy in order to improve the accuracy of fault diagnosis. Finally, we explain the engineered features and evaluate the selected models by using the Gain Chart and Area Under Curve (AUC) metrics. We use the hybrid expert system model to enhance maintenance planning decisions by assigning a health score to the railcar system of the North American Railcar Owner (NARO). According to the experimental results, our expert model can detect 96.4% of failures within 50% of the sample. This suggests that our method is effective at diagnosing failures in railcars fleet.

Risk-Averse Explore-Then-Commit Algorithms for Finite-Time Bandits

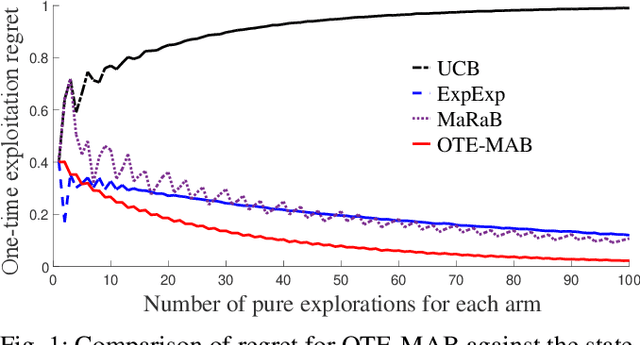
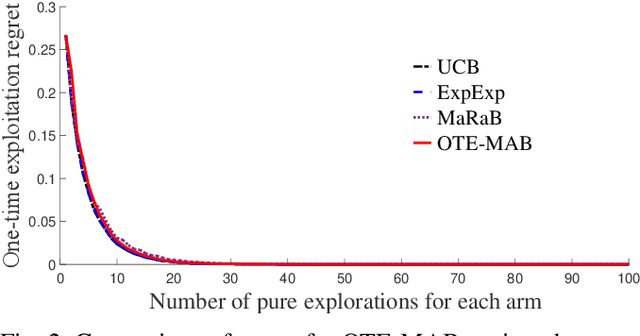
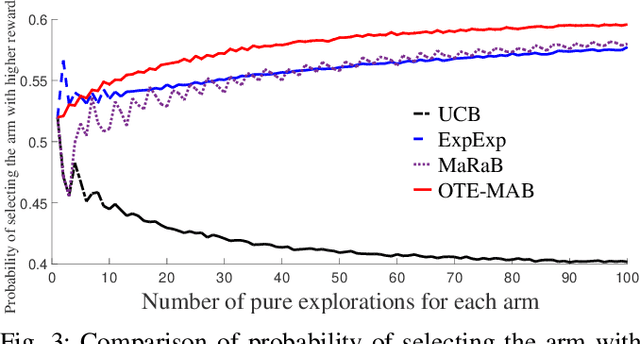
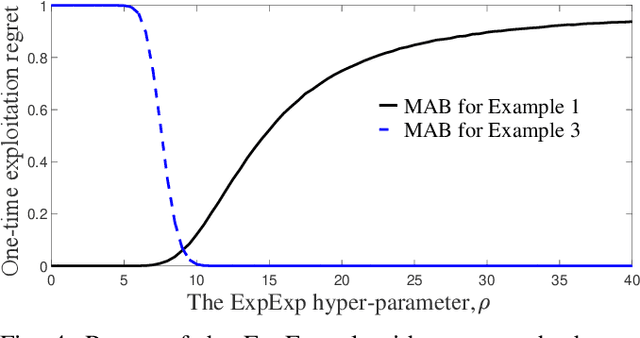
In this paper, we study multi-armed bandit problems in explore-then-commit setting. In our proposed explore-then-commit setting, the goal is to identify the best arm after a pure experimentation (exploration) phase and exploit it once or for a given finite number of times. We identify that although the arm with the highest expected reward is the most desirable objective for infinite exploitations, it is not necessarily the one that is most probable to have the highest reward in a single or finite-time exploitations. Alternatively, we advocate the idea of risk-aversion where the objective is to compete against the arm with the best risk-return trade-off. Then, we propose two algorithms whose objectives are to select the arm that is most probable to reward the most. Using a new notion of finite-time exploitation regret, we find an upper bound for the minimum number of experiments before commitment, to guarantee an upper bound for the regret. As compared to existing risk-averse bandit algorithms, our algorithms do not rely on hyper-parameters, resulting in a more robust behavior in practice, which is verified by the numerical evaluation.