Ali Yekkehkhany
Prob2Vec: Mathematical Semantic Embedding for Problem Retrieval in Adaptive Tutoring
Mar 21, 2020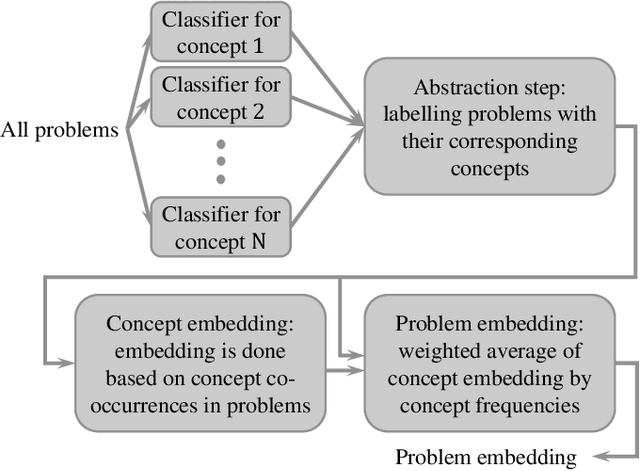
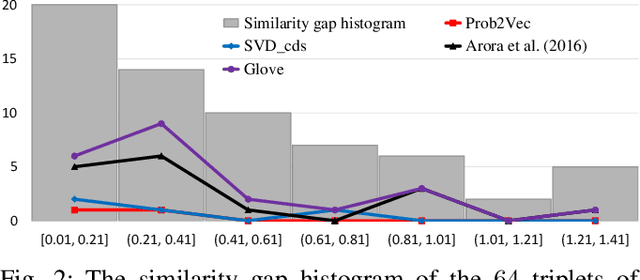
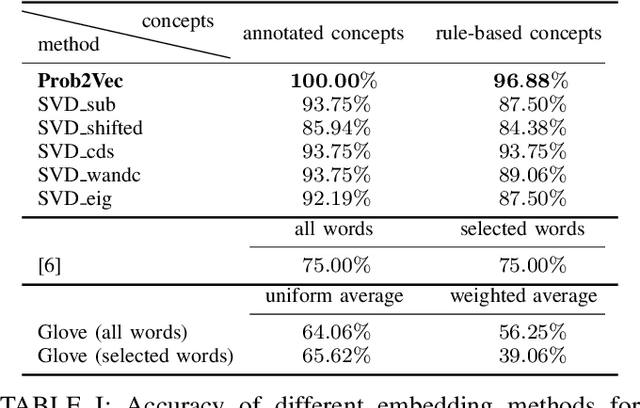
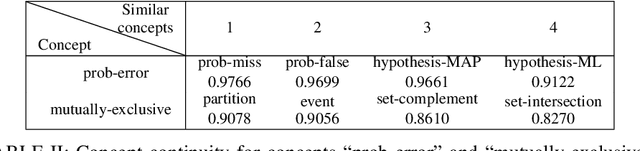
Abstract:We propose a new application of embedding techniques for problem retrieval in adaptive tutoring. The objective is to retrieve problems whose mathematical concepts are similar. There are two challenges: First, like sentences, problems helpful to tutoring are never exactly the same in terms of the underlying concepts. Instead, good problems mix concepts in innovative ways, while still displaying continuity in their relationships. Second, it is difficult for humans to determine a similarity score that is consistent across a large enough training set. We propose a hierarchical problem embedding algorithm, called Prob2Vec, that consists of abstraction and embedding steps. Prob2Vec achieves 96.88\% accuracy on a problem similarity test, in contrast to 75\% from directly applying state-of-the-art sentence embedding methods. It is interesting that Prob2Vec is able to distinguish very fine-grained differences among problems, an ability humans need time and effort to acquire. In addition, the sub-problem of concept labeling with imbalanced training data set is interesting in its own right. It is a multi-label problem suffering from dimensionality explosion, which we propose ways to ameliorate. We propose the novel negative pre-training algorithm that dramatically reduces false negative and positive ratios for classification, using an imbalanced training data set.
Risk-Averse Explore-Then-Commit Algorithms for Finite-Time Bandits
May 08, 2019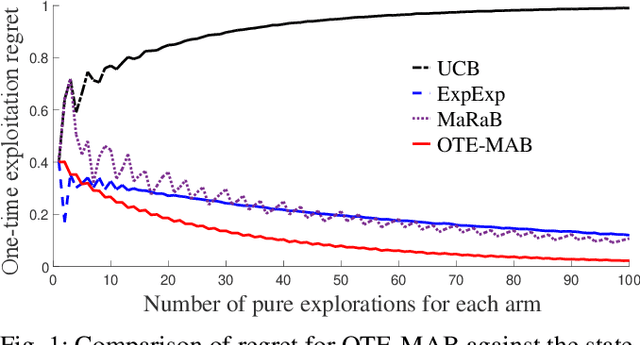
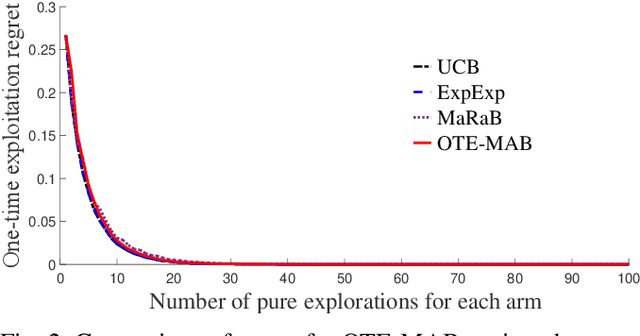
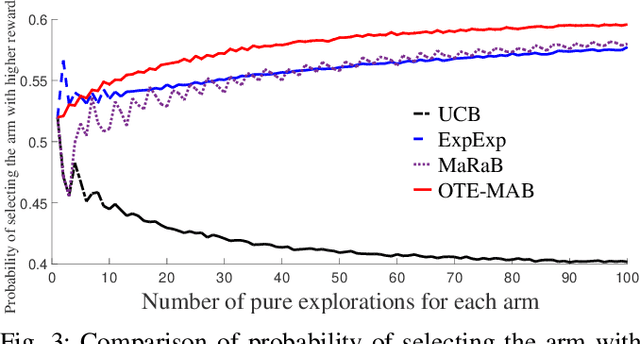
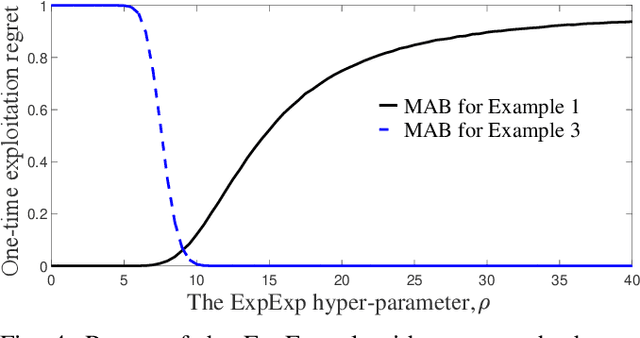
Abstract:In this paper, we study multi-armed bandit problems in explore-then-commit setting. In our proposed explore-then-commit setting, the goal is to identify the best arm after a pure experimentation (exploration) phase and exploit it once or for a given finite number of times. We identify that although the arm with the highest expected reward is the most desirable objective for infinite exploitations, it is not necessarily the one that is most probable to have the highest reward in a single or finite-time exploitations. Alternatively, we advocate the idea of risk-aversion where the objective is to compete against the arm with the best risk-return trade-off. Then, we propose two algorithms whose objectives are to select the arm that is most probable to reward the most. Using a new notion of finite-time exploitation regret, we find an upper bound for the minimum number of experiments before commitment, to guarantee an upper bound for the regret. As compared to existing risk-averse bandit algorithms, our algorithms do not rely on hyper-parameters, resulting in a more robust behavior in practice, which is verified by the numerical evaluation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge