Batch Bayesian Optimization for Replicable Experimental Design

Many real-world experimental design problems (a) evaluate multiple experimental conditions in parallel and (b) replicate each condition multiple times due to large and heteroscedastic observation noise. Given a fixed total budget, this naturally induces a trade-off between evaluating more unique conditions while replicating each of them fewer times vs. evaluating fewer unique conditions and replicating each more times. Moreover, in these problems, practitioners may be risk-averse and hence prefer an input with both good average performance and small variability. To tackle both challenges, we propose the Batch Thompson Sampling for Replicable Experimental Design (BTS-RED) framework, which encompasses three algorithms. Our BTS-RED-Known and BTS-RED-Unknown algorithms, for, respectively, known and unknown noise variance, choose the number of replications adaptively rather than deterministically such that an input with a larger noise variance is replicated more times. As a result, despite the noise heteroscedasticity, both algorithms enjoy a theoretical guarantee and are asymptotically no-regret. Our Mean-Var-BTS-RED algorithm aims at risk-averse optimization and is also asymptotically no-regret. We also show the effectiveness of our algorithms in two practical real-world applications: precision agriculture and AutoML.

Rectified Max-Value Entropy Search for Bayesian Optimization

Although the existing max-value entropy search (MES) is based on the widely celebrated notion of mutual information, its empirical performance can suffer due to two misconceptions whose implications on the exploration-exploitation trade-off are investigated in this paper. These issues are essential in the development of future acquisition functions and the improvement of the existing ones as they encourage an accurate measure of the mutual information such as the rectified MES (RMES) acquisition function we develop in this work. Unlike the evaluation of MES, we derive a closed-form probability density for the observation conditioned on the max-value and employ stochastic gradient ascent with reparameterization to efficiently optimize RMES. As a result of a more principled acquisition function, RMES shows a consistent improvement over MES in several synthetic function benchmarks and real-world optimization problems.

Markov Chain Monte Carlo-Based Machine Unlearning: Unlearning What Needs to be Forgotten

As the use of machine learning (ML) models is becoming increasingly popular in many real-world applications, there are practical challenges that need to be addressed for model maintenance. One such challenge is to 'undo' the effect of a specific subset of dataset used for training a model. This specific subset may contain malicious or adversarial data injected by an attacker, which affects the model performance. Another reason may be the need for a service provider to remove data pertaining to a specific user to respect the user's privacy. In both cases, the problem is to 'unlearn' a specific subset of the training data from a trained model without incurring the costly procedure of retraining the whole model from scratch. Towards this goal, this paper presents a Markov chain Monte Carlo-based machine unlearning (MCU) algorithm. MCU helps to effectively and efficiently unlearn a trained model from subsets of training dataset. Furthermore, we show that with MCU, we are able to explain the effect of a subset of a training dataset on the model prediction. Thus, MCU is useful for examining subsets of data to identify the adversarial data to be removed. Similarly, MCU can be used to erase the lineage of a user's personal data from trained ML models, thus upholding a user's "right to be forgotten". We empirically evaluate the performance of our proposed MCU algorithm on real-world phishing and diabetes datasets. Results show that MCU can achieve a desirable performance by efficiently removing the effect of a subset of training dataset and outperform an existing algorithm that utilizes the remaining dataset.

Trusted-Maximizers Entropy Search for Efficient Bayesian Optimization

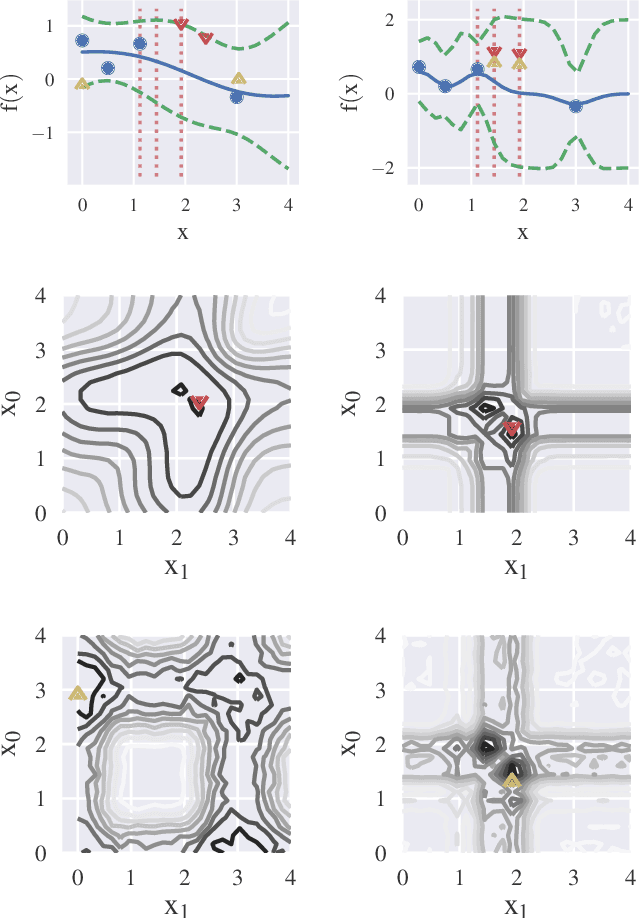
Information-based Bayesian optimization (BO) algorithms have achieved state-of-the-art performance in optimizing a black-box objective function. However, they usually require several approximations or simplifying assumptions (without clearly understanding their effects on the BO performance) and/or their generalization to batch BO is computationally unwieldy, especially with an increasing batch size. To alleviate these issues, this paper presents a novel trusted-maximizers entropy search (TES) acquisition function: It measures how much an input query contributes to the information gain on the maximizer over a finite set of trusted maximizers, i.e., inputs optimizing functions that are sampled from the Gaussian process posterior belief of the objective function. Evaluating TES requires either only a stochastic approximation with sampling or a deterministic approximation with expectation propagation, both of which are investigated and empirically evaluated using synthetic benchmark objective functions and real-world optimization problems, e.g., hyperparameter tuning of a convolutional neural network and synthesizing 'physically realizable' faces to fool a black-box face recognition system. Though TES can naturally be generalized to a batch variant with either approximation, the latter is amenable to be scaled to a much larger batch size in our experiments.

Value-at-Risk Optimization with Gaussian Processes

Value-at-risk (VaR) is an established measure to assess risks in critical real-world applications with random environmental factors. This paper presents a novel VaR upper confidence bound (V-UCB) algorithm for maximizing the VaR of a black-box objective function with the first no-regret guarantee. To realize this, we first derive a confidence bound of VaR and then prove the existence of values of the environmental random variable (to be selected to achieve no regret) such that the confidence bound of VaR lies within that of the objective function evaluated at such values. Our V-UCB algorithm empirically demonstrates state-of-the-art performance in optimizing synthetic benchmark functions, a portfolio optimization problem, and a simulated robot task.

An Information-Theoretic Framework for Unifying Active Learning Problems

This paper presents an information-theoretic framework for unifying active learning problems: level set estimation (LSE), Bayesian optimization (BO), and their generalized variant. We first introduce a novel active learning criterion that subsumes an existing LSE algorithm and achieves state-of-the-art performance in LSE problems with a continuous input domain. Then, by exploiting the relationship between LSE and BO, we design a competitive information-theoretic acquisition function for BO that has interesting connections to upper confidence bound and max-value entropy search (MES). The latter connection reveals a drawback of MES which has important implications on not only MES but also on other MES-based acquisition functions. Finally, our unifying information-theoretic framework can be applied to solve a generalized problem of LSE and BO involving multiple level sets in a data-efficient manner. We empirically evaluate the performance of our proposed algorithms using synthetic benchmark functions, a real-world dataset, and in hyperparameter tuning of machine learning models.

Top-$k$ Ranking Bayesian Optimization

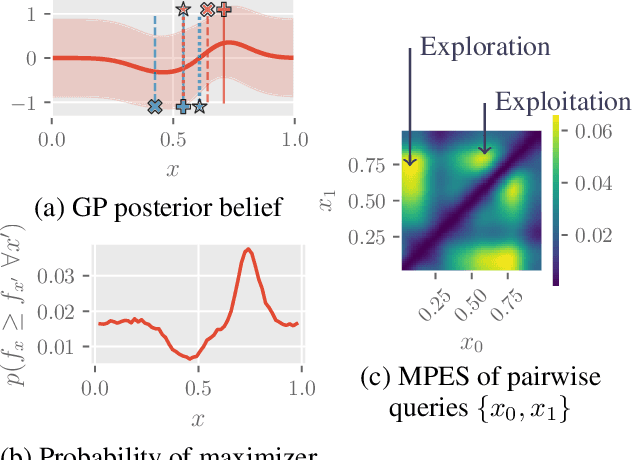
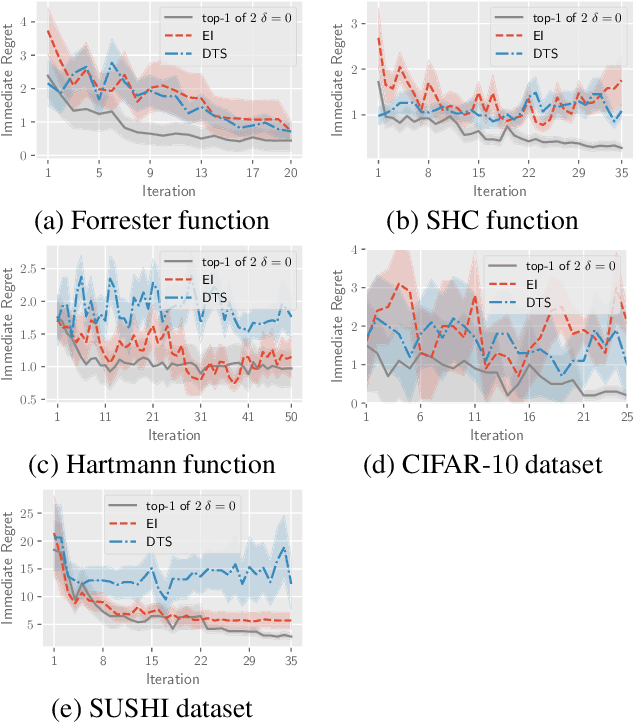
This paper presents a novel approach to top-$k$ ranking Bayesian optimization (top-$k$ ranking BO) which is a practical and significant generalization of preferential BO to handle top-$k$ ranking and tie/indifference observations. We first design a surrogate model that is not only capable of catering to the above observations, but is also supported by a classic random utility model. Another equally important contribution is the introduction of the first information-theoretic acquisition function in BO with preferential observation called multinomial predictive entropy search (MPES) which is flexible in handling these observations and optimized for all inputs of a query jointly. MPES possesses superior performance compared with existing acquisition functions that select the inputs of a query one at a time greedily. We empirically evaluate the performance of MPES using several synthetic benchmark functions, CIFAR-$10$ dataset, and SUSHI preference dataset.

Efficient Exploration of Reward Functions in Inverse Reinforcement Learning via Bayesian Optimization

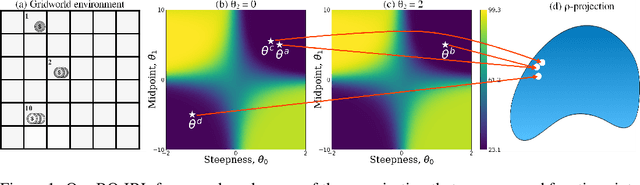
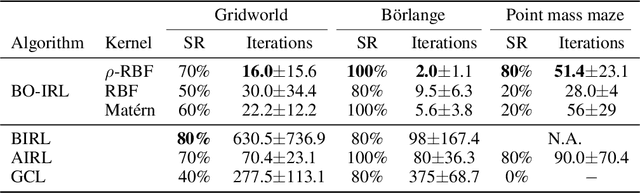
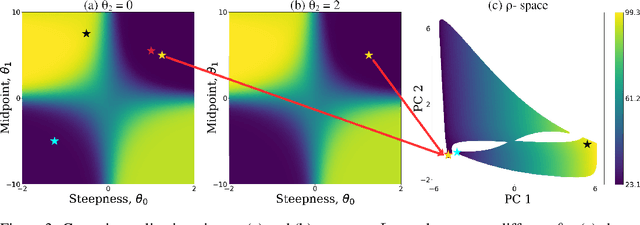
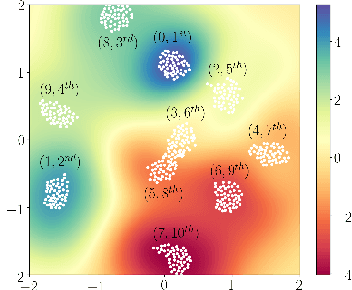
The problem of inverse reinforcement learning (IRL) is relevant to a variety of tasks including value alignment and robot learning from demonstration. Despite significant algorithmic contributions in recent years, IRL remains an ill-posed problem at its core; multiple reward functions coincide with the observed behavior and the actual reward function is not identifiable without prior knowledge or supplementary information. This paper presents an IRL framework called Bayesian optimization-IRL (BO-IRL) which identifies multiple solutions that are consistent with the expert demonstrations by efficiently exploring the reward function space. BO-IRL achieves this by utilizing Bayesian Optimization along with our newly proposed kernel that (a) projects the parameters of policy invariant reward functions to a single point in a latent space and (b) ensures nearby points in the latent space correspond to reward functions yielding similar likelihoods. This projection allows the use of standard stationary kernels in the latent space to capture the correlations present across the reward function space. Empirical results on synthetic and real-world environments (model-free and model-based) show that BO-IRL discovers multiple reward functions while minimizing the number of expensive exact policy optimizations.

Variational Bayesian Unlearning

This paper studies the problem of approximately unlearning a Bayesian model from a small subset of the training data to be erased. We frame this problem as one of minimizing the Kullback-Leibler divergence between the approximate posterior belief of model parameters after directly unlearning from erased data vs. the exact posterior belief from retraining with remaining data. Using the variational inference (VI) framework, we show that it is equivalent to minimizing an evidence upper bound which trades off between fully unlearning from erased data vs. not entirely forgetting the posterior belief given the full data (i.e., including the remaining data); the latter prevents catastrophic unlearning that can render the model useless. In model training with VI, only an approximate (instead of exact) posterior belief given the full data can be obtained, which makes unlearning even more challenging. We propose two novel tricks to tackle this challenge. We empirically demonstrate our unlearning methods on Bayesian models such as sparse Gaussian process and logistic regression using synthetic and real-world datasets.

Inverse Reinforcement Learning with Missing Data

We consider the problem of recovering an expert's reward function with inverse reinforcement learning (IRL) when there are missing/incomplete state-action pairs or observations in the demonstrated trajectories. This issue of missing trajectory data or information occurs in many situations, e.g., GPS signals from vehicles moving on a road network are intermittent. In this paper, we propose a tractable approach to directly compute the log-likelihood of demonstrated trajectories with incomplete/missing data. Our algorithm is efficient in handling a large number of missing segments in the demonstrated trajectories, as it performs the training with incomplete data by solving a sequence of systems of linear equations, and the number of such systems to be solved does not depend on the number of missing segments. Empirical evaluation on a real-world dataset shows that our training algorithm outperforms other conventional techniques.