Batch Bayesian Optimization for Replicable Experimental Design

Many real-world experimental design problems (a) evaluate multiple experimental conditions in parallel and (b) replicate each condition multiple times due to large and heteroscedastic observation noise. Given a fixed total budget, this naturally induces a trade-off between evaluating more unique conditions while replicating each of them fewer times vs. evaluating fewer unique conditions and replicating each more times. Moreover, in these problems, practitioners may be risk-averse and hence prefer an input with both good average performance and small variability. To tackle both challenges, we propose the Batch Thompson Sampling for Replicable Experimental Design (BTS-RED) framework, which encompasses three algorithms. Our BTS-RED-Known and BTS-RED-Unknown algorithms, for, respectively, known and unknown noise variance, choose the number of replications adaptively rather than deterministically such that an input with a larger noise variance is replicated more times. As a result, despite the noise heteroscedasticity, both algorithms enjoy a theoretical guarantee and are asymptotically no-regret. Our Mean-Var-BTS-RED algorithm aims at risk-averse optimization and is also asymptotically no-regret. We also show the effectiveness of our algorithms in two practical real-world applications: precision agriculture and AutoML.

Incentivizing Collaboration in Machine Learning via Synthetic Data Rewards

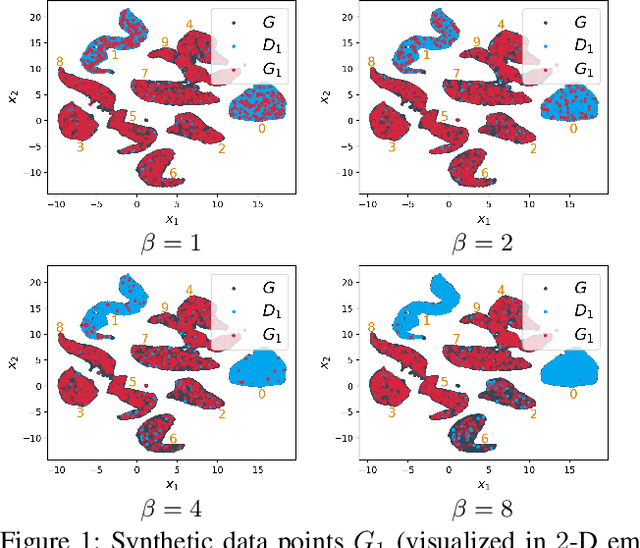
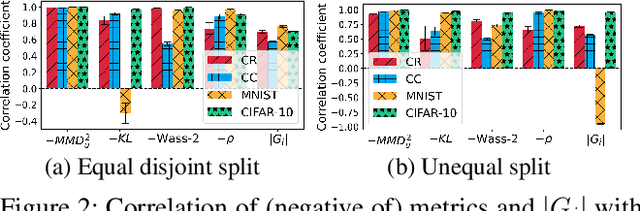
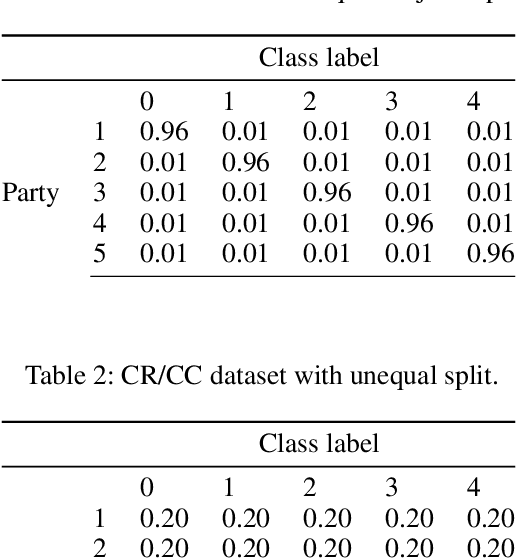
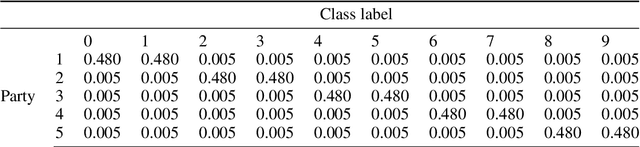
This paper presents a novel collaborative generative modeling (CGM) framework that incentivizes collaboration among self-interested parties to contribute data to a pool for training a generative model (e.g., GAN), from which synthetic data are drawn and distributed to the parties as rewards commensurate to their contributions. Distributing synthetic data as rewards (instead of trained models or money) offers task- and model-agnostic benefits for downstream learning tasks and is less likely to violate data privacy regulation. To realize the framework, we firstly propose a data valuation function using maximum mean discrepancy (MMD) that values data based on its quantity and quality in terms of its closeness to the true data distribution and provide theoretical results guiding the kernel choice in our MMD-based data valuation function. Then, we formulate the reward scheme as a linear optimization problem that when solved, guarantees certain incentives such as fairness in the CGM framework. We devise a weighted sampling algorithm for generating synthetic data to be distributed to each party as reward such that the value of its data and the synthetic data combined matches its assigned reward value by the reward scheme. We empirically show using simulated and real-world datasets that the parties' synthetic data rewards are commensurate to their contributions.