Top-$k$ Ranking Bayesian Optimization
Paper and Code
Dec 19, 2020
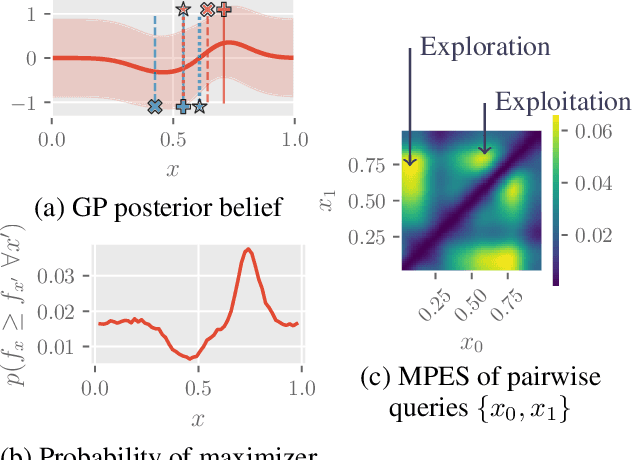
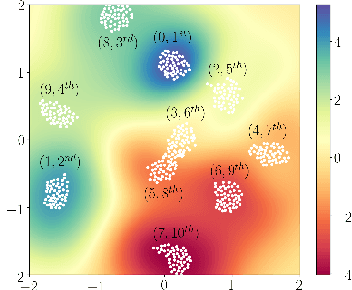
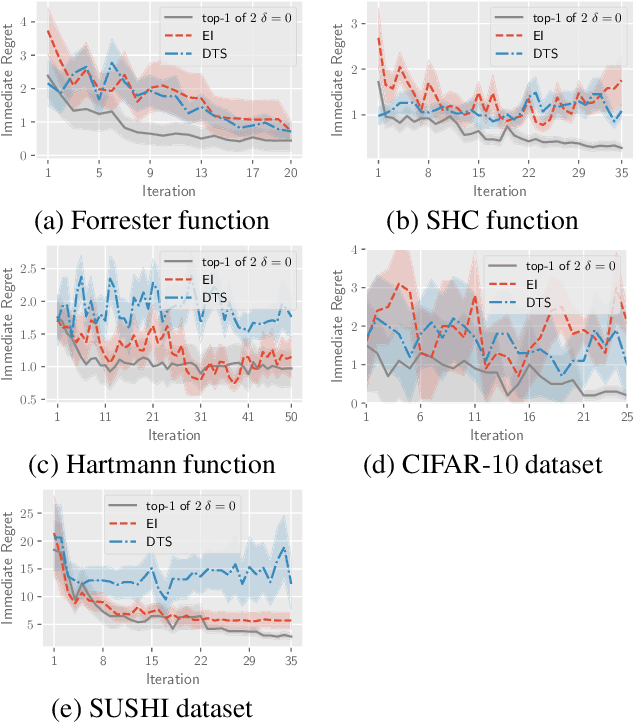
This paper presents a novel approach to top-$k$ ranking Bayesian optimization (top-$k$ ranking BO) which is a practical and significant generalization of preferential BO to handle top-$k$ ranking and tie/indifference observations. We first design a surrogate model that is not only capable of catering to the above observations, but is also supported by a classic random utility model. Another equally important contribution is the introduction of the first information-theoretic acquisition function in BO with preferential observation called multinomial predictive entropy search (MPES) which is flexible in handling these observations and optimized for all inputs of a query jointly. MPES possesses superior performance compared with existing acquisition functions that select the inputs of a query one at a time greedily. We empirically evaluate the performance of MPES using several synthetic benchmark functions, CIFAR-$10$ dataset, and SUSHI preference dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge