A Computational Efficient Maximum Likelihood Direct Position Determination Approach for Multiple Emitters Using Angle and Doppler Measurements

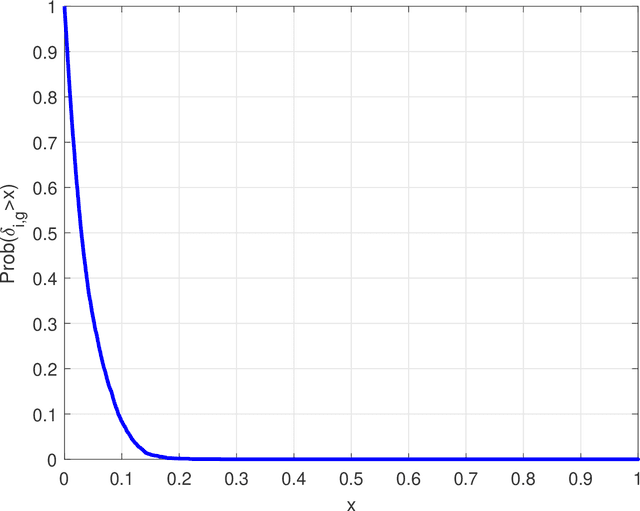
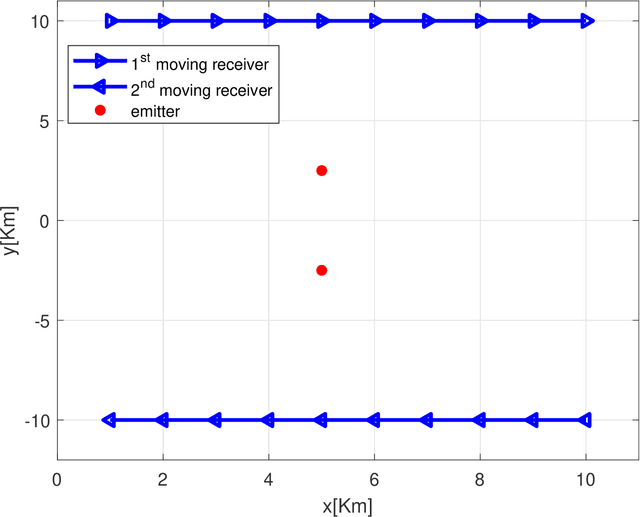
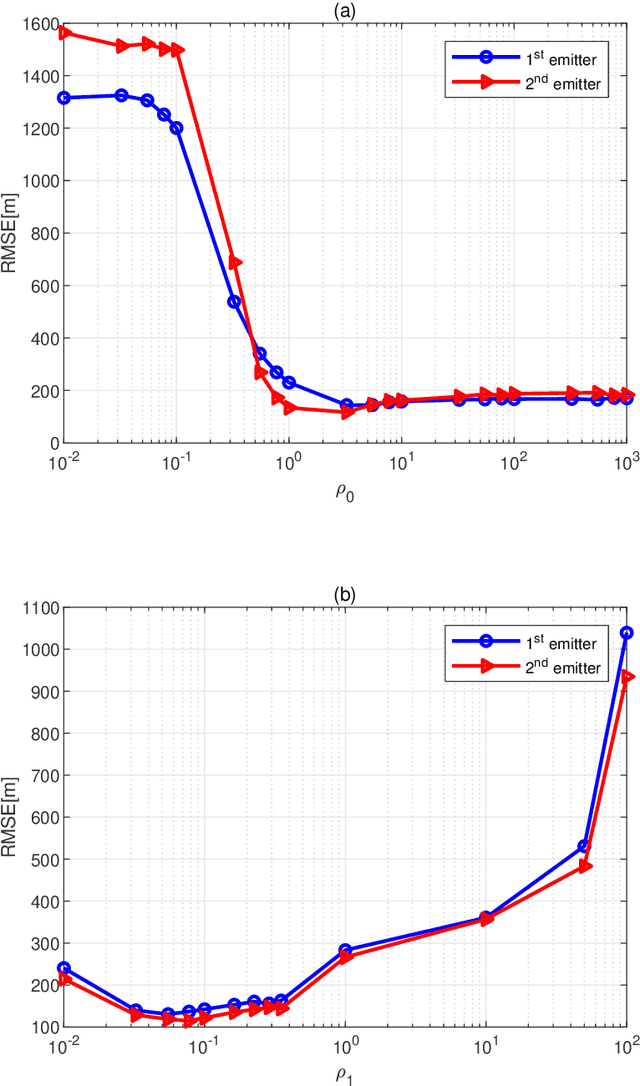
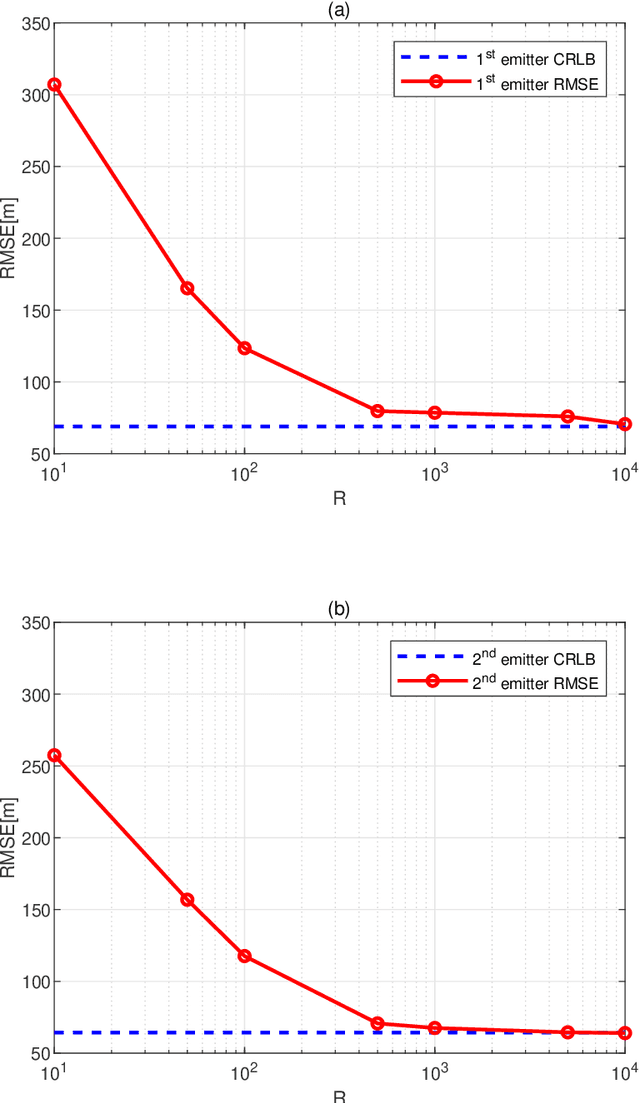
Emitter localization is widely applied in the military and civilian _elds. In this paper, we tackle the problem of position estimation for multiple stationary emitters using Doppler frequency shifts and angles by moving receivers. The computational load for the exhaustive maximum likelihood (ML) direct position determination (DPD) search is insu_erable. Based on the Pincus' theorem and importance sampling (IS) concept, we propose a novel non-iterative ML DPD method. The proposed method transforms the original multidimensional grid search into random variables generation with multiple low-dimensional pseudo-probability density functions (PDF), and the circular mean is used for superior position estimation performance. The computational complexity of the proposed method is modest, and the o_-grid problem that most existing DPD techniques face is signi_cantly alleviated. Moreover, it can be implemented in parallel separately. Simulation results demonstrate that the proposed ML DPD estimator can achieve better estimation accuracy than state-of-the-art DPD techniques. With a reasonable parameter choice, the estimation performance of the proposed technique is very close to the Cram_er-Rao lower bound (CRLB), even in the adverse conditions of low signal-to-noise ratios (SNR) levels.

Complex Orthogonal Matching Pursuit and Its Exact Recovery Conditions

In this paper, we present new results on using orthogonal matching pursuit (OMP), to solve the sparse approximation problem over redundant dictionaries for complex cases (i.e., complex measurement vector, complex dictionary and complex additive white Gaussian noise (CAWGN)). A sufficient condition that OMP can recover the optimal representation of an exactly sparse signal in the complex cases is proposed both in noiseless and bound Gaussian noise settings. Similar to exact recovery condition (ERC) results in real cases, we extend them to complex case and derivate the corresponding ERC in the paper. It leverages this theory to show that OMP succeed for k-sparse signal from a class of complex dictionary. Besides, an application with geometrical theory of diffraction (GTD) model is presented for complex cases. Finally, simulation experiments illustrate the validity of the theoretical analysis.