Rapid and Accurate Diagnosis of Acute Aortic Syndrome using Non-contrast CT: A Large-scale, Retrospective, Multi-center and AI-based Study

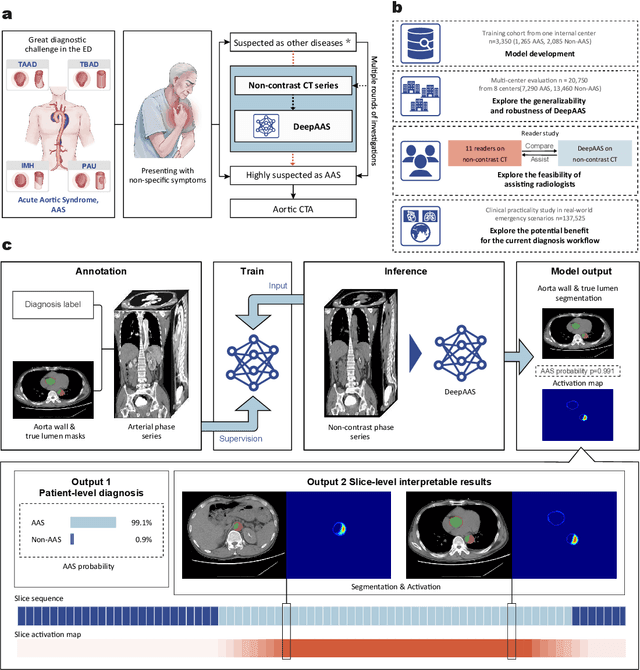
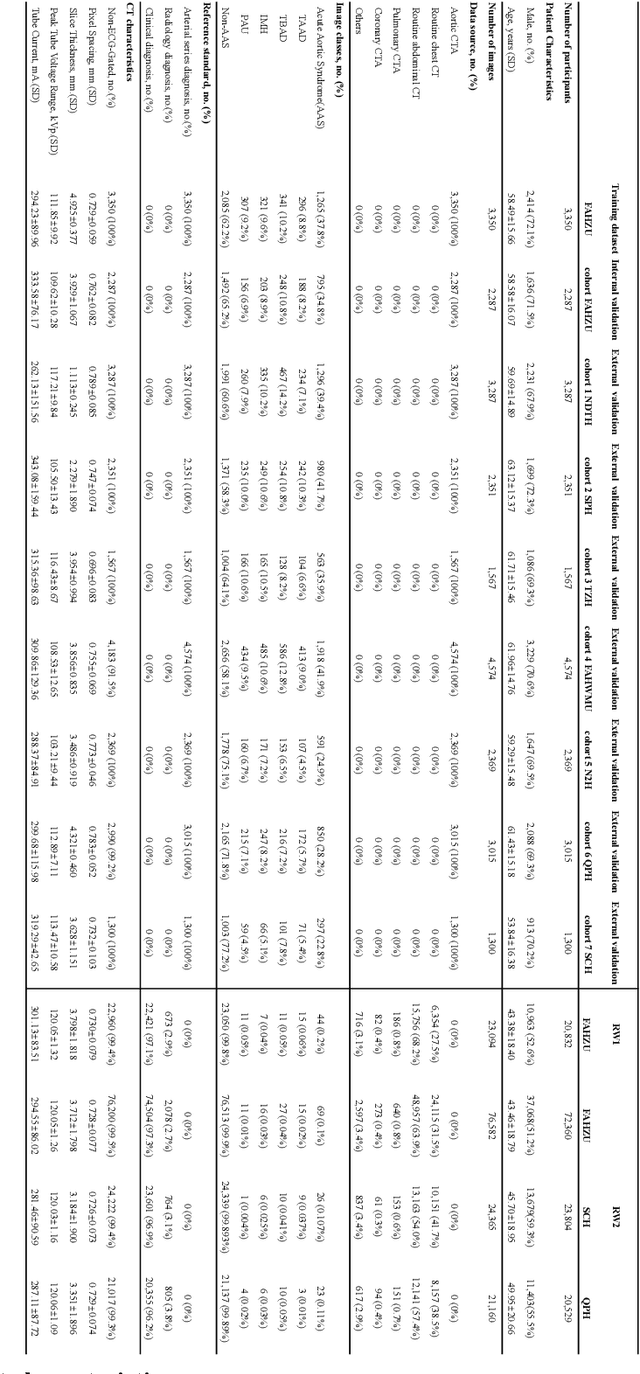
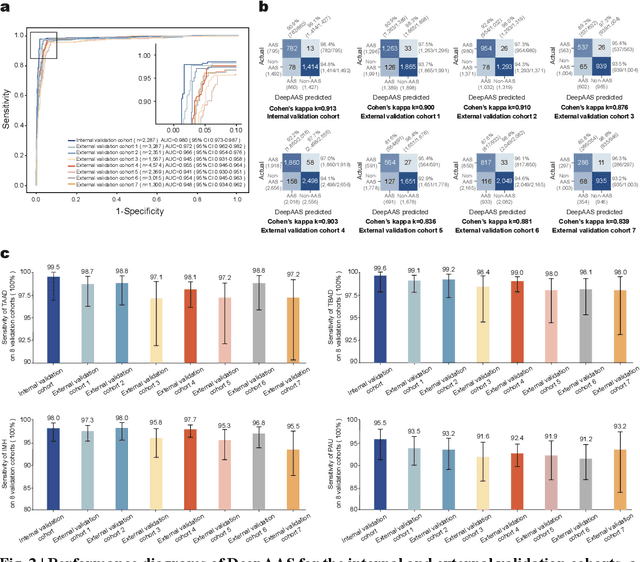
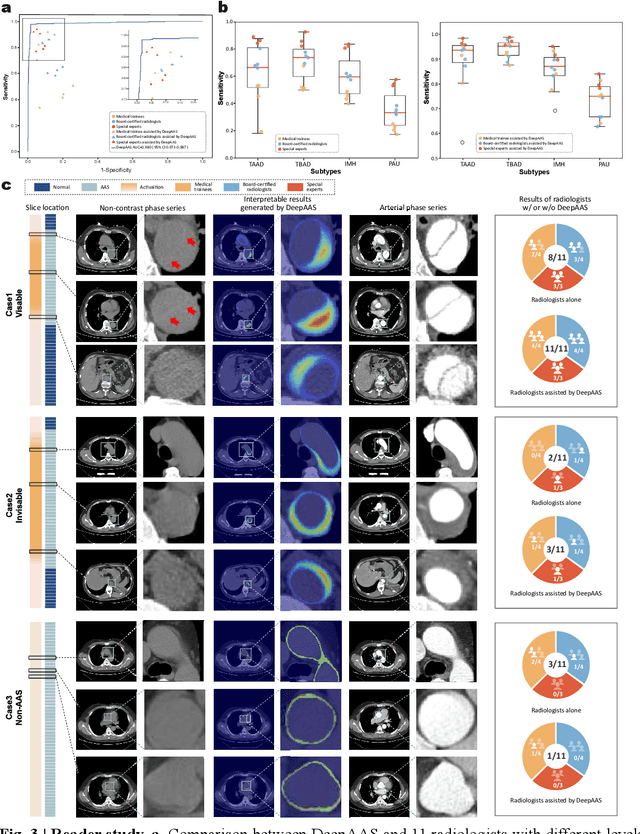
Chest pain symptoms are highly prevalent in emergency departments (EDs), where acute aortic syndrome (AAS) is a catastrophic cardiovascular emergency with a high fatality rate, especially when timely and accurate treatment is not administered. However, current triage practices in the ED can cause up to approximately half of patients with AAS to have an initially missed diagnosis or be misdiagnosed as having other acute chest pain conditions. Subsequently, these AAS patients will undergo clinically inaccurate or suboptimal differential diagnosis. Fortunately, even under these suboptimal protocols, nearly all these patients underwent non-contrast CT covering the aorta anatomy at the early stage of differential diagnosis. In this study, we developed an artificial intelligence model (DeepAAS) using non-contrast CT, which is highly accurate for identifying AAS and provides interpretable results to assist in clinical decision-making. Performance was assessed in two major phases: a multi-center retrospective study (n = 20,750) and an exploration in real-world emergency scenarios (n = 137,525). In the multi-center cohort, DeepAAS achieved a mean area under the receiver operating characteristic curve of 0.958 (95% CI 0.950-0.967). In the real-world cohort, DeepAAS detected 109 AAS patients with misguided initial suspicion, achieving 92.6% (95% CI 76.2%-97.5%) in mean sensitivity and 99.2% (95% CI 99.1%-99.3%) in mean specificity. Our AI model performed well on non-contrast CT at all applicable early stages of differential diagnosis workflows, effectively reduced the overall missed diagnosis and misdiagnosis rate from 48.8% to 4.8% and shortened the diagnosis time for patients with misguided initial suspicion from an average of 681.8 (74-11,820) mins to 68.5 (23-195) mins. DeepAAS could effectively fill the gap in the current clinical workflow without requiring additional tests.

TDANet: A Novel Temporal Denoise Convolutional Neural Network With Attention for Fault Diagnosis

Fault diagnosis plays a crucial role in maintaining the operational integrity of mechanical systems, preventing significant losses due to unexpected failures. As intelligent manufacturing and data-driven approaches evolve, Deep Learning (DL) has emerged as a pivotal technique in fault diagnosis research, recognized for its ability to autonomously extract complex features. However, the practical application of current fault diagnosis methods is challenged by the complexity of industrial environments. This paper proposed the Temporal Denoise Convolutional Neural Network With Attention (TDANet), designed to improve fault diagnosis performance in noise environments. This model transforms one-dimensional signals into two-dimensional tensors based on their periodic properties, employing multi-scale 2D convolution kernels to extract signal information both within and across periods. This method enables effective identification of signal characteristics that vary over multiple time scales. The TDANet incorporates a Temporal Variable Denoise (TVD) module with residual connections and a Multi-head Attention Fusion (MAF) module, enhancing the saliency of information within noisy data and maintaining effective fault diagnosis performance. Evaluation on two datasets, CWRU (single sensor) and Real aircraft sensor fault (multiple sensors), demonstrates that the TDANet model significantly outperforms existing deep learning approaches in terms of diagnostic accuracy under noisy environments.

Complex Orthogonal Matching Pursuit and Its Exact Recovery Conditions

In this paper, we present new results on using orthogonal matching pursuit (OMP), to solve the sparse approximation problem over redundant dictionaries for complex cases (i.e., complex measurement vector, complex dictionary and complex additive white Gaussian noise (CAWGN)). A sufficient condition that OMP can recover the optimal representation of an exactly sparse signal in the complex cases is proposed both in noiseless and bound Gaussian noise settings. Similar to exact recovery condition (ERC) results in real cases, we extend them to complex case and derivate the corresponding ERC in the paper. It leverages this theory to show that OMP succeed for k-sparse signal from a class of complex dictionary. Besides, an application with geometrical theory of diffraction (GTD) model is presented for complex cases. Finally, simulation experiments illustrate the validity of the theoretical analysis.