Quantitative Analysis of Molecular Transport in the Extracellular Space Using Physics-Informed Neural Network

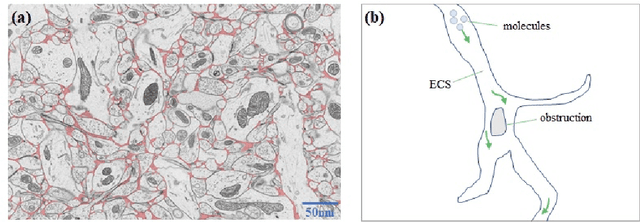
The brain extracellular space (ECS), an irregular, extremely tortuous nanoscale space located between cells or between cells and blood vessels, is crucial for nerve cell survival. It plays a pivotal role in high-level brain functions such as memory, emotion, and sensation. However, the specific form of molecular transport within the ECS remain elusive. To address this challenge, this paper proposes a novel approach to quantitatively analyze the molecular transport within the ECS by solving an inverse problem derived from the advection-diffusion equation (ADE) using a physics-informed neural network (PINN). PINN provides a streamlined solution to the ADE without the need for intricate mathematical formulations or grid settings. Additionally, the optimization of PINN facilitates the automatic computation of the diffusion coefficient governing long-term molecule transport and the velocity of molecules driven by advection. Consequently, the proposed method allows for the quantitative analysis and identification of the specific pattern of molecular transport within the ECS through the calculation of the Peclet number. Experimental validation on two datasets of magnetic resonance images (MRIs) captured at different time points showcases the effectiveness of the proposed method. Notably, our simulations reveal identical molecular transport patterns between datasets representing rats with tracer injected into the same brain region. These findings highlight the potential of PINN as a promising tool for comprehensively exploring molecular transport within the ECS.

Bloch Equation Enables Physics-informed Neural Network in Parametric Magnetic Resonance Imaging

Magnetic resonance imaging (MRI) is an important non-invasive imaging method in clinical diagnosis. Beyond the common image structures, parametric imaging can provide the intrinsic tissue property thus could be used in quantitative evaluation. The emerging deep learning approach provides fast and accurate parameter estimation but still encounters the lack of network interpretation and enough training data. Even with a large amount of training data, the mismatch between the training and target data may introduce errors. Here, we propose one way that solely relies on the target scanned data and does not need a pre-defined training database. We provide a proof-of-concept that embeds the physical rule of MRI, the Bloch equation, into the loss of physics-informed neural network (PINN). PINN enables learning the Bloch equation, estimating the T2 parameter, and generating a series of physically synthetic data. Experimental results are conducted on phantom and cardiac imaging to demonstrate its potential in quantitative MRI.

Physics-informed deep diffusion MRI reconstruction: break the bottleneck of training data in artificial intelligence

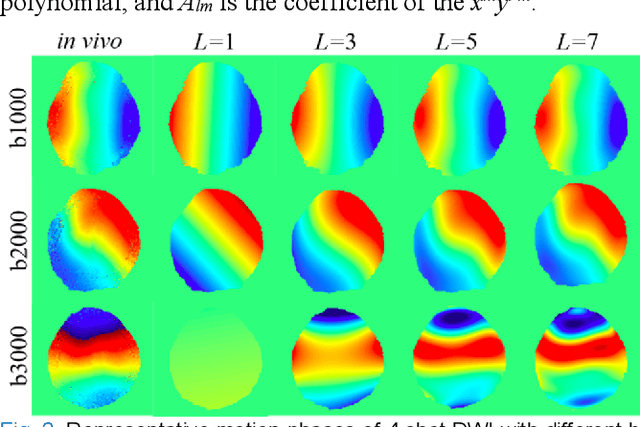
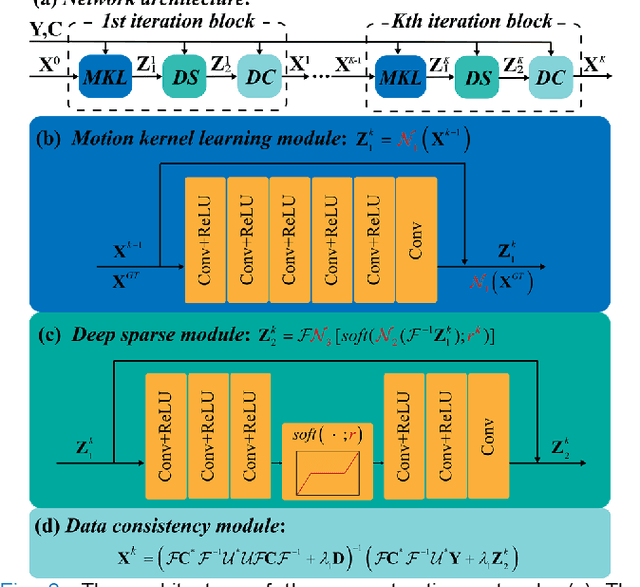
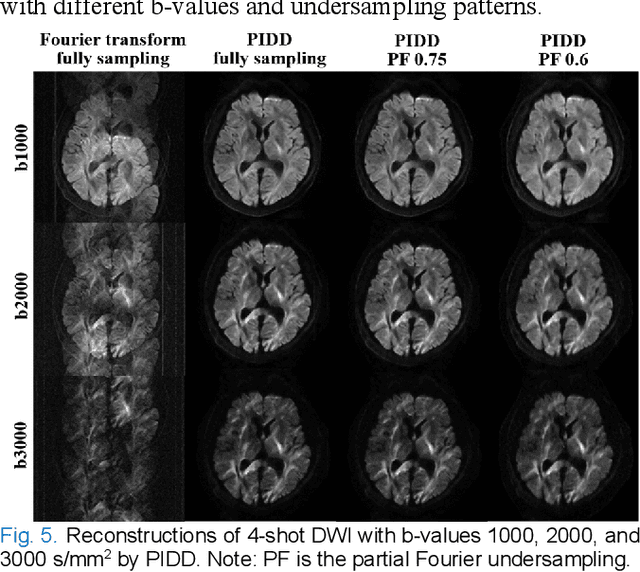
In this work, we propose a Physics-Informed Deep Diffusion magnetic resonance imaging (DWI) reconstruction method (PIDD). PIDD contains two main components: The multi-shot DWI data synthesis and a deep learning reconstruction network. For data synthesis, we first mathematically analyze the motion during the multi-shot data acquisition and approach it by a simplified physical motion model. The motion model inspires a polynomial model for motion-induced phase synthesis. Then, lots of synthetic phases are combined with a few real data to generate a large amount of training data. For reconstruction network, we exploit the smoothness property of each shot image phase as learnable convolution kernels in the k-space and complementary sparsity in the image domain. Results on both synthetic and in vivo brain data show that, the proposed PIDD trained on synthetic data enables sub-second ultra-fast, high-quality, and robust reconstruction with different b-values and undersampling patterns.