Machine Learning as an Accurate Predictor for Percolation Threshold of Diverse Networks

Percolation threshold is an important measure to determine the inherent rigidity of large networks. Predictors of the percolation threshold for large networks are computationally intense to run, hence it is a necessity to develop predictors of the percolation threshold of networks, that do not rely on numerical simulations. We demonstrate the efficacy of five machine learning-based regression techniques for the accurate prediction of the percolation threshold. The dataset generated to train the machine learning models contains a total of 777 real and synthetic networks and consists of 5 statistical and structural properties of networks as features and the numerically computed percolation threshold as the output attribute. We establish that the machine learning models outperform three existing empirical estimators of bond percolation threshold, and extend this experiment to predict site and explosive percolation. We also compare the performance of our models in predicting the percolation threshold and find that the gradient boosting regressor, multilayer perceptron and random forests regression models achieve the least RMSE values among the models utilized.

Application of S-Transform on Hyper kurtosis based Modified Duo Histogram Equalized DIC images for Pre-cancer Detection

Our proposed hyper kurtosis based histogram equalized DIC images enhances the contrast by preserving the brightness. The evolution and development of precancerous activity among tissues are studied through S-transform (ST). The significant variations of amplitude spectra can be observed due to increased medium roughness from normal tissue were observed in time-frequency domain. The randomness and inhomogeneity of the tissue structures among human normal and different grades of DIC tissues is recognized by ST based timefrequency analysis. This study offers a simpler and better way to recognize the substantial changes among different stages of DIC tissues, which are reflected by spatial information containing within the inhomogeneity structures of different types of tissue.

A comparative study between proposed Hyper Kurtosis based Modified Duo-Histogram Equalization (HKMDHE) and Contrast Limited Adaptive Histogram Equalization (CLAHE) for Contrast Enhancement Purpose of Low Contrast Human Brain CT scan images

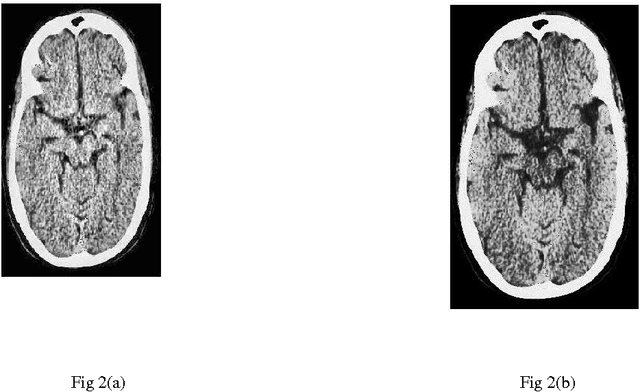
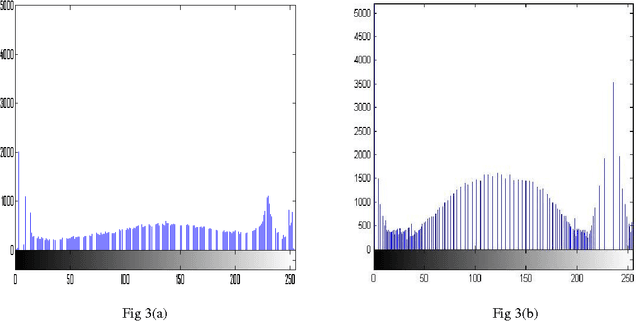
In this paper, a comparative study between proposed hyper kurtosis based modified duo-histogram equalization (HKMDHE) algorithm and contrast limited adaptive histogram enhancement (CLAHE) has been presented for the implementation of contrast enhancement and brightness preservation of low contrast human brain CT scan images. In HKMDHE algorithm, contrast enhancement is done on the hyper-kurtosis based application. The results are very promising of proposed HKMDHE technique with improved PSNR values and lesser AMMBE values than CLAHE technique.

Wavelet based approach for tissue fractal parameter measurement: Pre cancer detection

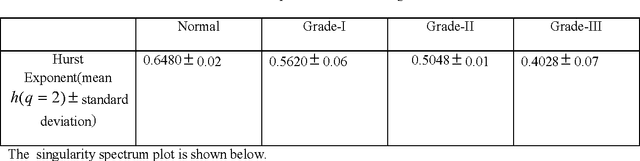
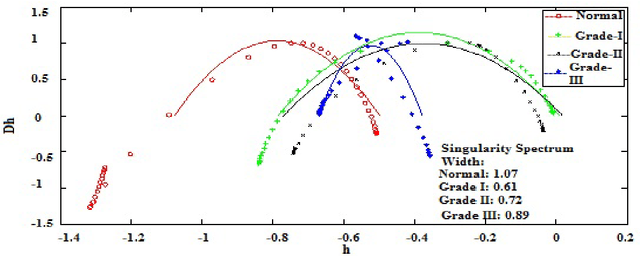
In this paper, we have carried out the detail studies of pre-cancer by wavelet coherency and multifractal based detrended fluctuation analysis (MFDFA) on differential interference contrast (DIC) images of stromal region among different grades of pre-cancer tissues. Discrete wavelet transform (DWT) through Daubechies basis has been performed for identifying fluctuations over polynomial trends for clear characterization and differentiation of tissues. Wavelet coherence plots are performed for identifying the level of correlation in time scale plane between normal and various grades of DIC samples. Applying MFDFA on refractive index variations of cervical tissues, we have observed that the values of Hurst exponent (correlation) decreases from healthy (normal) to pre-cancer tissues. The width of singularity spectrum has a sudden degradation at grade-I in comparison of healthy (normal) tissue but later on it increases as cancer progresses from grade-II to grade-III.

An Adaptive Statistical Non-uniform Quantizer for Detail Wavelet Components in Lossy JPEG2000 Image Compression

The paper presents a non-uniform quantization method for the Detail components in the JPEG2000 standard. Incorporating the fact that the coefficients lying towards the ends of the histogram plot of each Detail component represent the structural information of an image, the quantization step sizes become smaller at they approach the ends of the histogram plot. The variable quantization step sizes are determined by the actual statistics of the wavelet coefficients. Mean and standard deviation are the two statistical parameters used iteratively to obtain the variable step sizes. Moreover, the mean of the coefficients lying within the step size is chosen as the quantized value, contrary to the deadzone uniform quantizer which selects the midpoint of the quantization step size as the quantized value. The experimental results of the deadzone uniform quantizer and the proposed non-uniform quantizer are objectively compared by using Mean-Squared Error (MSE) and Mean Structural Similarity Index Measure (MSSIM), to evaluate the quantization error and reconstructed image quality, respectively. Subjective analysis of the reconstructed images is also carried out. Through the objective and subjective assessments, it is shown that the non-uniform quantizer performs better than the deadzone uniform quantizer in the perceptual quality of the reconstructed image, especially at low bitrates. More importantly, unlike the deadzone uniform quantizer, the non-uniform quantizer accomplishes better visual quality with a few quantized values.

A Semi-automated Statistical Algorithm for Object Separation

We explicate a semi-automated statistical algorithm for object identification and segregation in both gray scale and color images. The algorithm makes optimal use of the observation that definite objects in an image are typically represented by pixel values having narrow Gaussian distributions about characteristic mean values. Furthermore, for visually distinct objects, the corresponding Gaussian distributions have negligible overlap with each other and hence the Mahalanobis distance between these distributions are large. These statistical facts enable one to sub-divide images into multiple thresholds of variable sizes, each segregating similar objects. The procedure incorporates the sensitivity of human eye to the gray pixel values into the variable threshold size, while mapping the Gaussian distributions into localized \delta-functions, for object separation. The effectiveness of this recursive statistical algorithm is demonstrated using a wide variety of images.

Multisegmentation through wavelets: Comparing the efficacy of Daubechies vs Coiflets

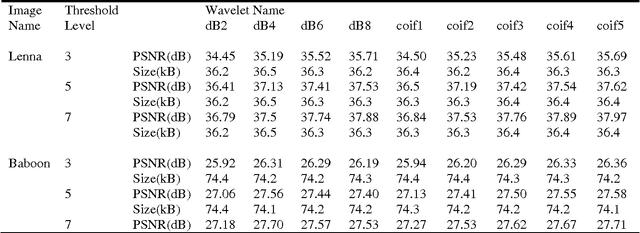
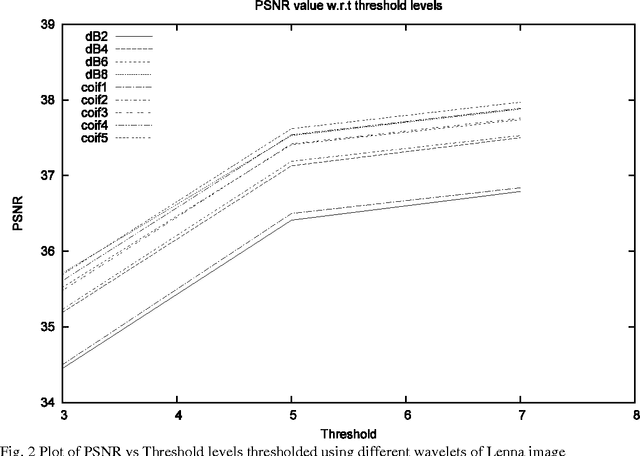
In this paper, we carry out a comparative study of the efficacy of wavelets belonging to Daubechies and Coiflet family in achieving image segmentation through a fast statistical algorithm.The fact that wavelets belonging to Daubechies family optimally capture the polynomial trends and those of Coiflet family satisfy mini-max condition, makes this comparison interesting. In the context of the present algorithm, it is found that the performance of Coiflet wavelets is better, as compared to Daubechies wavelet.

A Fast Statistical Method for Multilevel Thresholding in Wavelet Domain

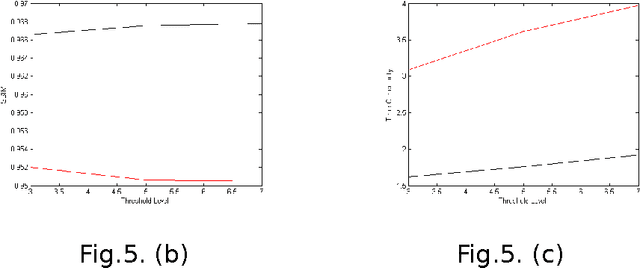
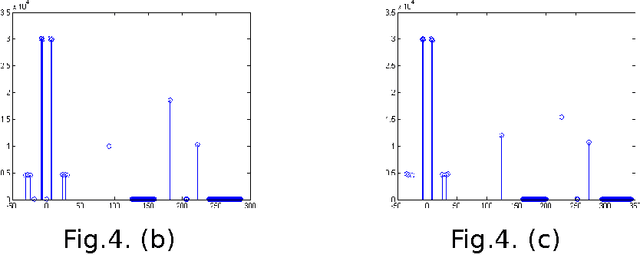
An algorithm is proposed for the segmentation of image into multiple levels using mean and standard deviation in the wavelet domain. The procedure provides for variable size segmentation with bigger block size around the mean, and having smaller blocks at the ends of histogram plot of each horizontal, vertical and diagonal components, while for the approximation component it provides for finer block size around the mean, and larger blocks at the ends of histogram plot coefficients. It is found that the proposed algorithm has significantly less time complexity, achieves superior PSNR and Structural Similarity Measurement Index as compared to similar space domain algorithms[1]. In the process it highlights finer image structures not perceptible in the original image. It is worth emphasizing that after the segmentation only 16 (at threshold level 3) wavelet coefficients captures the significant variation of image.

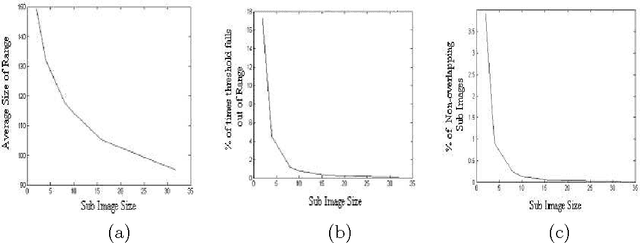
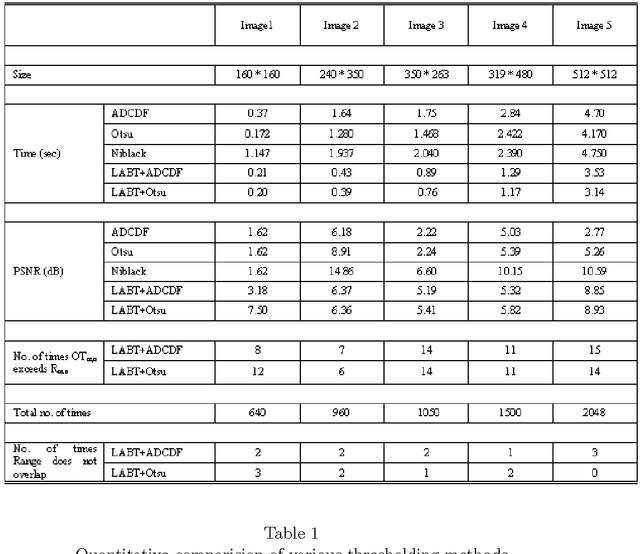
Locally Adaptive Block Thresholding Method with Continuity Constraint

We present an algorithm that enables one to perform locally adaptive block thresholding, while maintaining image continuity. Images are divided into sub-images based some standard image attributes and thresholding technique is employed over the sub-images. The present algorithm makes use of the thresholds of neighboring sub-images to calculate a range of values. The image continuity is taken care by choosing the threshold of the sub-image under consideration to lie within the above range. After examining the average range values for various sub-image sizes of a variety of images, it was found that the range of acceptable threshold values is substantially high, justifying our assumption of exploiting the freedom of range for bringing out local details.

Multilevel Thresholding for Image Segmentation through a Fast Statistical Recursive Algorithm

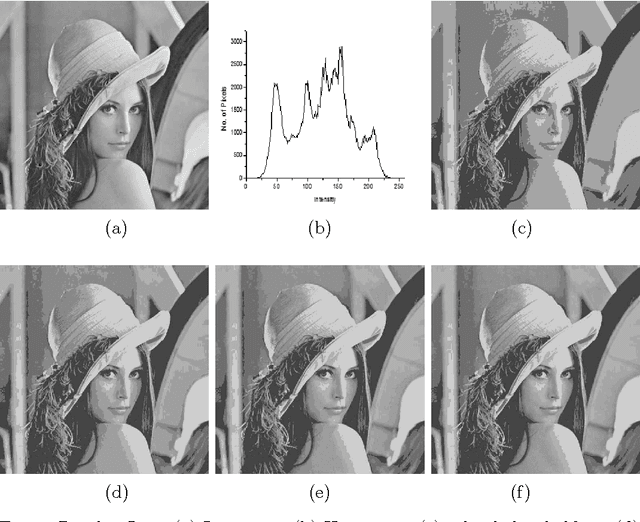
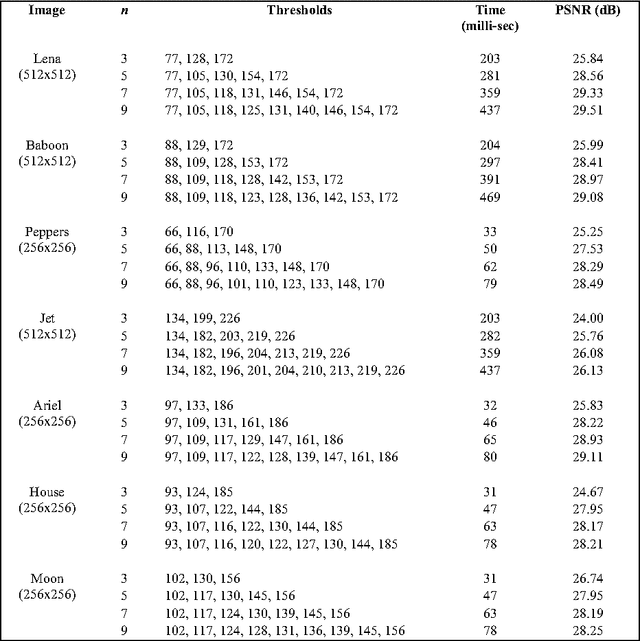
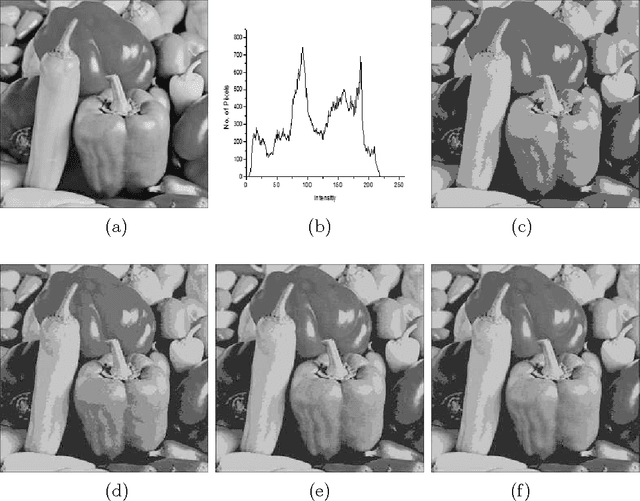
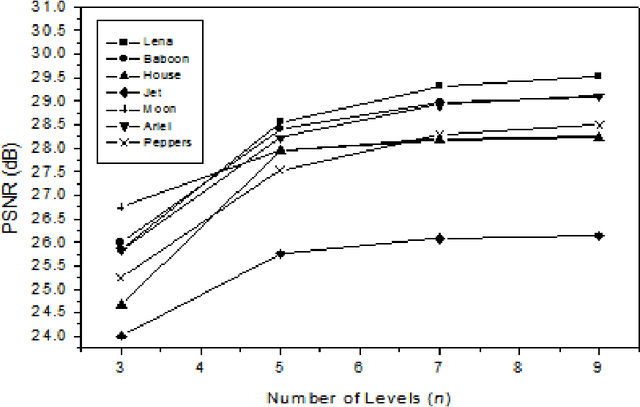
A novel algorithm is proposed for segmenting an image into multiple levels using its mean and variance. Starting from the extreme pixel values at both ends of the histogram plot, the algorithm is applied recursively on sub-ranges computed from the previous step, so as to find a threshold level and a new sub-range for the next step, until no significant improvement in image quality can be achieved. The method makes use of the fact that a number of distributions tend towards Dirac delta function, peaking at the mean, in the limiting condition of vanishing variance. The procedure naturally provides for variable size segmentation with bigger blocks near the extreme pixel values and finer divisions around the mean or other chosen value for better visualization. Experiments on a variety of images show that the new algorithm effectively segments the image in computationally very less time.