Amit Verma
Enhancing Fluorescence Lifetime Parameter Estimation Accuracy with Differential Transformer Based Deep Learning Model Incorporating Pixelwise Instrument Response Function
Nov 25, 2024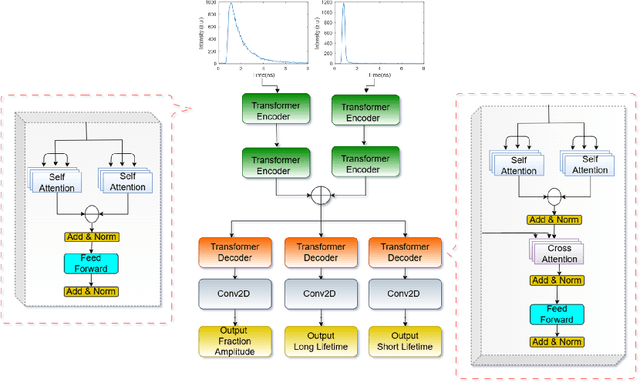
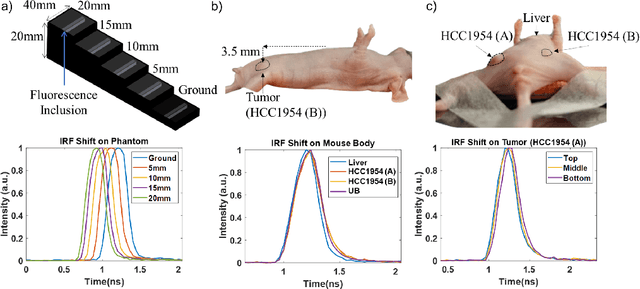
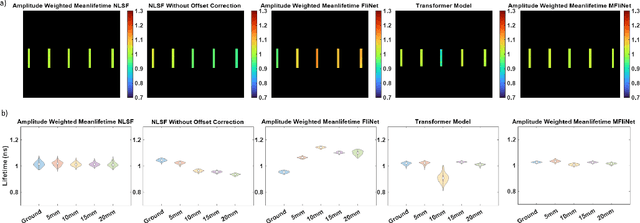
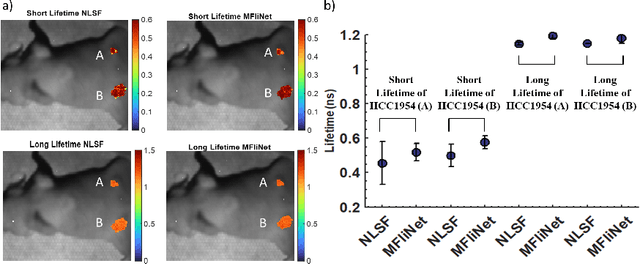
Abstract:Fluorescence lifetime imaging (FLI) is an important molecular imaging modality that can provide unique information for biomedical applications. FLI is based on acquiring and processing photon time of arrival histograms. The shape and temporal offset of these histograms depends on many factors, such as the instrument response function (IRF), optical properties, and the topographic profile of the sample. Several inverse solver analytical methods have been developed to compute the underlying fluorescence lifetime parameters, but most of them are computationally expensive and time-consuming. Thus, deep learning (DL) algorithms have progressively replaced computation methods in fluorescence lifetime parameter estimation. Often, DL models are trained with simple datasets either generated through simulation or a simple experiment where the fluorophore surface profile is mostly flat; therefore, DL models often do not perform well on samples with complex surface profiles such as ex-vivo organs or in-vivo whole intact animals. Herein, we introduce a new DL architecture using state-of-the-art Differential Transformer encoder-decoder architecture, MFliNet (Macroscopic FLI Network), that takes an additional input of IRF together with TPSF, addressing discrepancies in the photon time-of-arrival distribution. We demonstrate the model's performance through carefully designed, complex tissue-mimicking phantoms and preclinical in-vivo cancer xenograft experiments.
Real-time Deformation Correction in Additively Printed Flexible Antenna Arrays
Jun 12, 2024Abstract:Conformal phased arrays provide multiple degrees of freedom to the scan angle, which is typically limited by antenna aperture in rigid arrays. Silicon-based RF signal processing offers reliable, reconfigurable, multi-functional, and compact control for conformal phased arrays that can be used for on-the-move communication. While the lightweight, compactness, and shape-changing properties of the conformal phased arrays are attractive, these features result in dynamic deformation of the array during motion leading to significant dynamic beam pointing errors. We propose a silicon-based, compact, reconfigurable solution to self-correct these dynamic deformation-induced beam pointing errors. Furthermore, additive printing is leveraged to enhance the flexibility of the conformal phased arrays, as the printed conductive ink is more flexible than bulk copper and can be easily deposited on flexible sheets using different printing tools, providing an environmentally-friendly solution for large-scale production. The inks such as conventional silver inks are expensive and copper-based printable inks suffer from spontaneous metal oxidation that alters trace impedance and degrades beamforming performance. This work uses a low-cost molecular copper decomposition ink with reliable RF properties at different temperature and strain to print the proposed intelligent conformal phased array operating at 2.1 GHz. Proof-of-concept prototype $2\times2$ array self-corrects the deformation induces beampointing error with an error $<1.25^\circ$. The silicon based array processing part occupying only 2.56 mm$^2$ area and 78.5 mW power per tile.
Efficient QUBO transformation for Higher Degree Pseudo Boolean Functions
Jul 24, 2021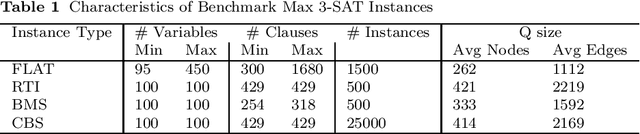
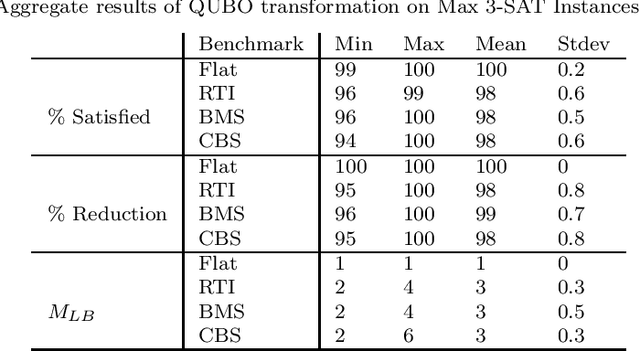
Abstract:Quadratic Unconstrained Binary Optimization (QUBO) is recognized as a unifying framework for modeling a wide range of problems. Problems can be solved with commercial solvers customized for solving QUBO and since QUBO have degree two, it is useful to have a method for transforming higher degree pseudo-Boolean problems to QUBO format. The standard transformation approach requires additional auxiliary variables supported by penalty terms for each higher degree term. This paper improves on the existing cubic-to-quadratic transformation approach by minimizing the number of additional variables as well as penalty coefficient. Extensive experimental testing on Max 3-SAT modeled as QUBO shows a near 100% reduction in the subproblem size used for minimization of the number of auxiliary variables.
QUBO transformation using Eigenvalue Decomposition
Jun 19, 2021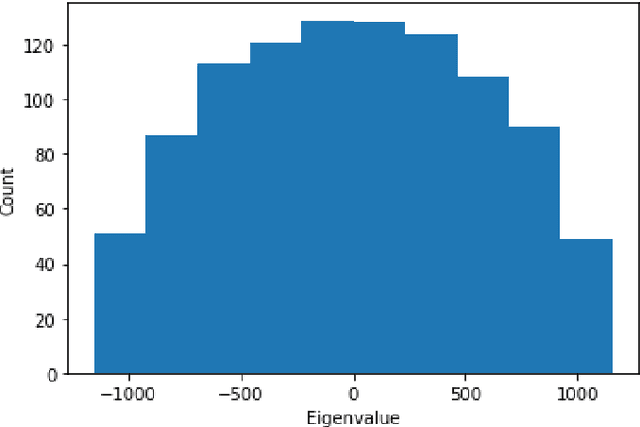
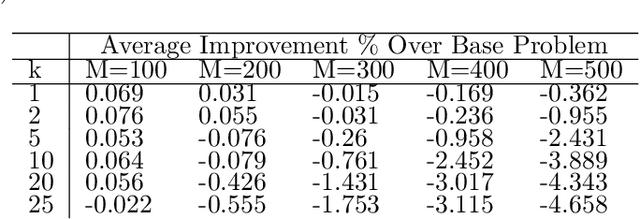
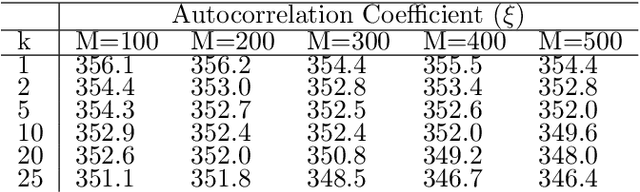
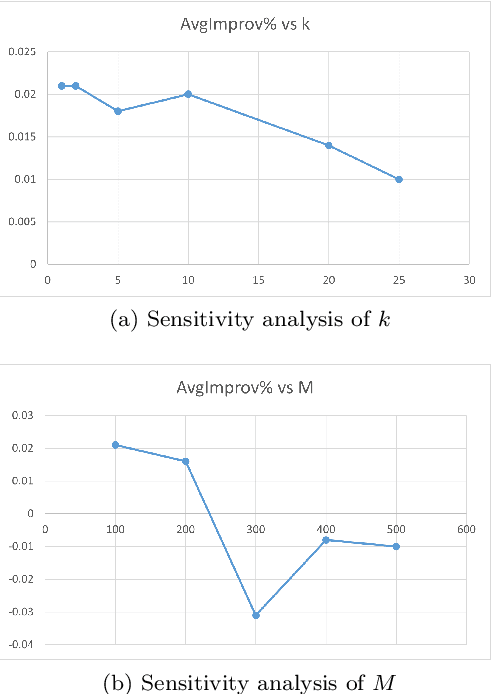
Abstract:Quadratic Unconstrained Binary Optimization (QUBO) is a general-purpose modeling framework for combinatorial optimization problems and is a requirement for quantum annealers. This paper utilizes the eigenvalue decomposition of the underlying Q matrix to alter and improve the search process by extracting the information from dominant eigenvalues and eigenvectors to implicitly guide the search towards promising areas of the solution landscape. Computational results on benchmark datasets illustrate the efficacy of our routine demonstrating significant performance improvements on problems with dominant eigenvalues.
Predicting 3D RNA Folding Patterns via Quadratic Binary Optimization
Jun 14, 2021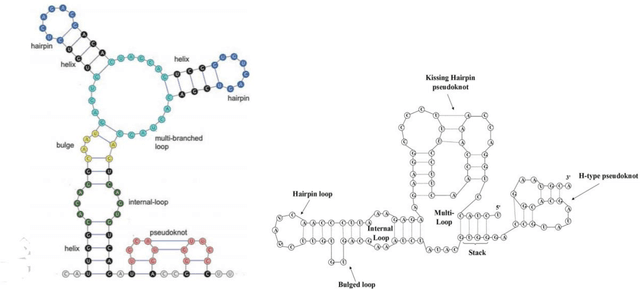
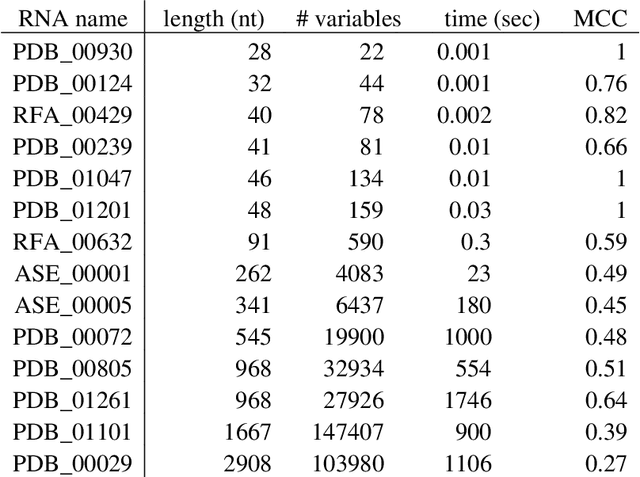
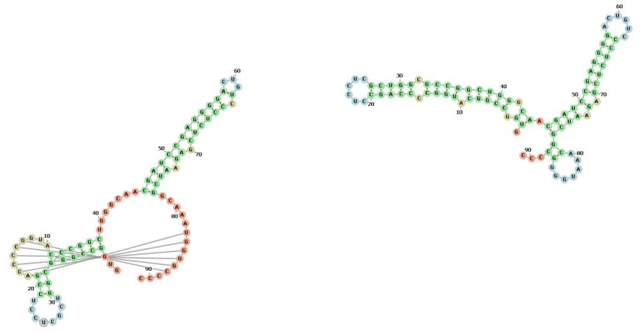

Abstract:The structure of an RNA molecule plays a significant role in its biological function. Predicting structure given a one dimensional sequence of RNA nucleotide bases is a difficult and important problem. Many computer programs (known as in silico) are available for predicting 2-dimensional (secondary) structures however 3-dimensional (tertiary) structure prediction is much more difficult mainly due to the far greater number of feasible solutions and fewer experimental data on the thermodynamic energies of 3D structures. It is also challenging to verify the most likely three dimensional structure even with the availability of sophisticated x-ray crystallography and nuclear magnetic resonance imaging technologies. In this paper we develop three dimensional RNA folding predictions by adding penalty and reward parameters to a previous two dimensional approach based on Quadratic Unconstrained Binary Optimization (QUBO) models. These parameters provide flexibility in the amount of three dimensional folding allowed. We address the problem of multiple near-optimal structures via a new weighted similarity structure measure and illustrate folding pathways via progressively improving local optimal solutions. The problems are solved via a new commercial QUBO solver AlphaQUBO (Meta-Analytics, 2020) that solves problems having hundreds of thousands of binary variables.
Constraint Programming to Discover One-Flip Local Optima of Quadratic Unconstrained Binary Optimization Problems
Apr 04, 2021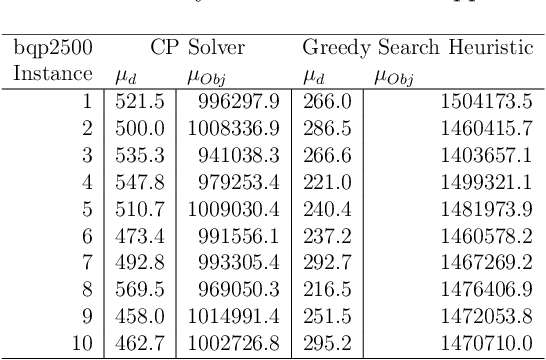
Abstract:The broad applicability of Quadratic Unconstrained Binary Optimization (QUBO) constitutes a general-purpose modeling framework for combinatorial optimization problems and are a required format for gate array and quantum annealing computers. QUBO annealers as well as other solution approaches benefit from starting with a diverse set of solutions with local optimality an additional benefit. This paper presents a new method for generating a set of one-flip local optima leveraging constraint programming. Further, as demonstrated in experimental testing, analysis of the solution set allows the generation of soft constraints to help guide the optimization process.
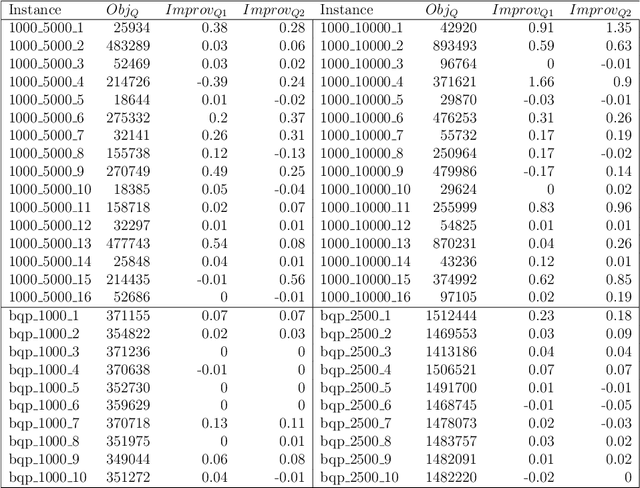
Goal Seeking Quadratic Unconstrained Binary Optimization
Mar 24, 2021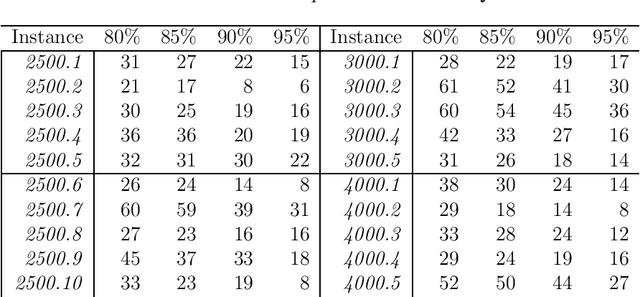
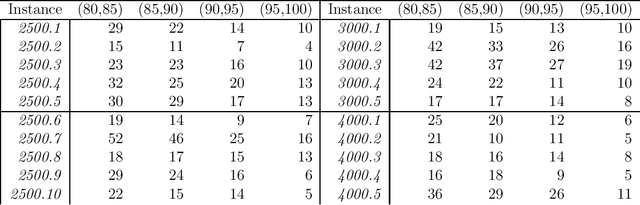
Abstract:The Quadratic Unconstrained Binary Optimization (QUBO) modeling and solution framework is required for quantum and digital annealers whose goal is the optimization of a well defined metric, the objective function. However, diverse suboptimal solutions may be preferred over harder to implement strict optimal ones. In addition, the decision-maker usually has insights that are not always efficiently translated into the optimization model, such as acceptable target, interval or range values. Multi-criteria decision making is an example of involving the user in the decision process. In this paper, we present two variants of goal-seeking QUBO that minimize the deviation from the goal through a tabu-search based greedy one-flip heuristic. Experimental results illustrate the efficacy of the proposed approach over Constraint Programming for quickly finding a satisficing set of solutions.
Locally Adaptive Block Thresholding Method with Continuity Constraint
Mar 09, 2006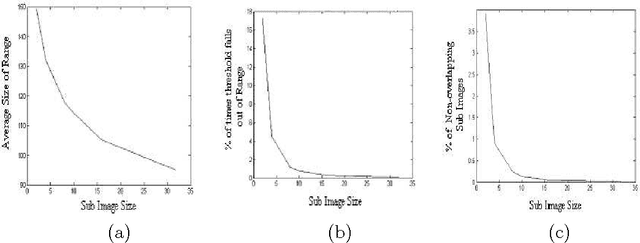
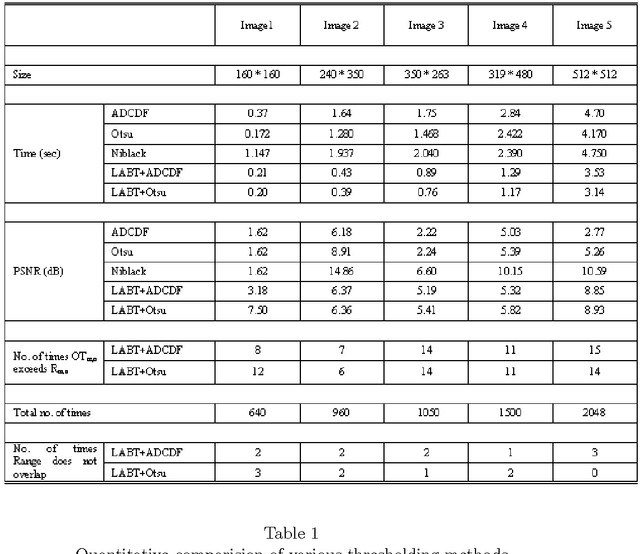


Abstract:We present an algorithm that enables one to perform locally adaptive block thresholding, while maintaining image continuity. Images are divided into sub-images based some standard image attributes and thresholding technique is employed over the sub-images. The present algorithm makes use of the thresholds of neighboring sub-images to calculate a range of values. The image continuity is taken care by choosing the threshold of the sub-image under consideration to lie within the above range. After examining the average range values for various sub-image sizes of a variety of images, it was found that the range of acceptable threshold values is substantially high, justifying our assumption of exploiting the freedom of range for bringing out local details.
Multilevel Thresholding for Image Segmentation through a Fast Statistical Recursive Algorithm
Feb 12, 2006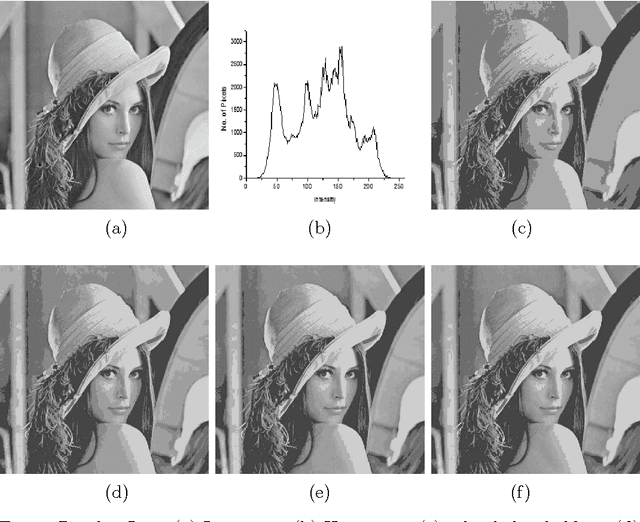
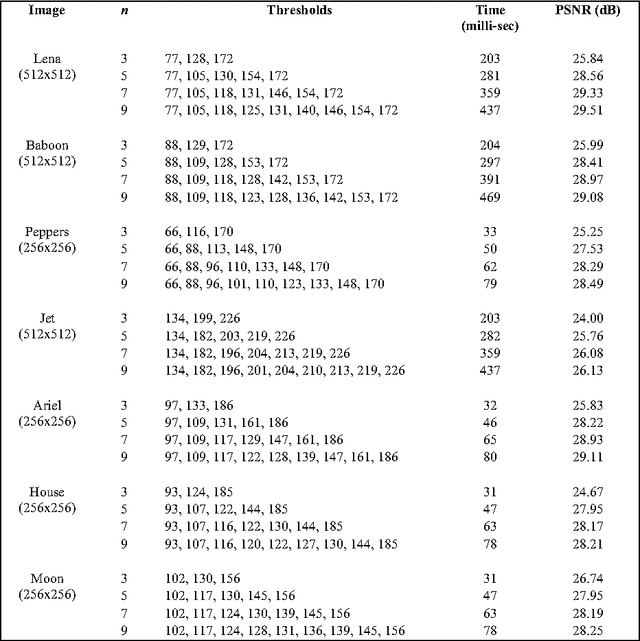
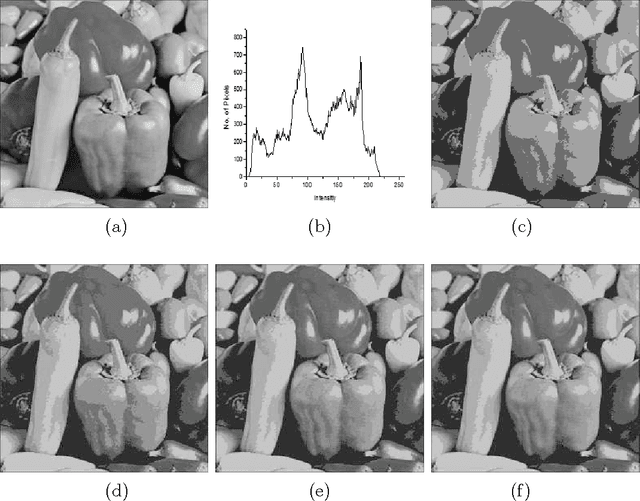
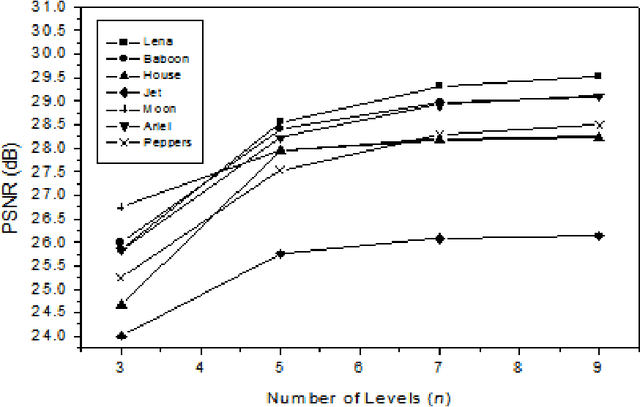
Abstract:A novel algorithm is proposed for segmenting an image into multiple levels using its mean and variance. Starting from the extreme pixel values at both ends of the histogram plot, the algorithm is applied recursively on sub-ranges computed from the previous step, so as to find a threshold level and a new sub-range for the next step, until no significant improvement in image quality can be achieved. The method makes use of the fact that a number of distributions tend towards Dirac delta function, peaking at the mean, in the limiting condition of vanishing variance. The procedure naturally provides for variable size segmentation with bigger blocks near the extreme pixel values and finer divisions around the mean or other chosen value for better visualization. Experiments on a variety of images show that the new algorithm effectively segments the image in computationally very less time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge