Multisegmentation through wavelets: Comparing the efficacy of Daubechies vs Coiflets

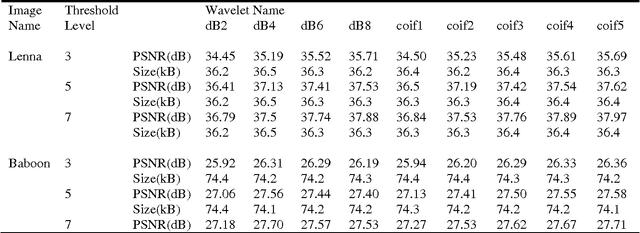
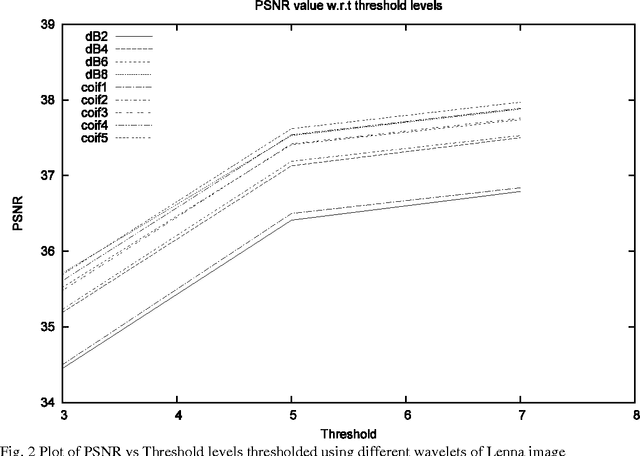
In this paper, we carry out a comparative study of the efficacy of wavelets belonging to Daubechies and Coiflet family in achieving image segmentation through a fast statistical algorithm.The fact that wavelets belonging to Daubechies family optimally capture the polynomial trends and those of Coiflet family satisfy mini-max condition, makes this comparison interesting. In the context of the present algorithm, it is found that the performance of Coiflet wavelets is better, as compared to Daubechies wavelet.

A Fast Statistical Method for Multilevel Thresholding in Wavelet Domain

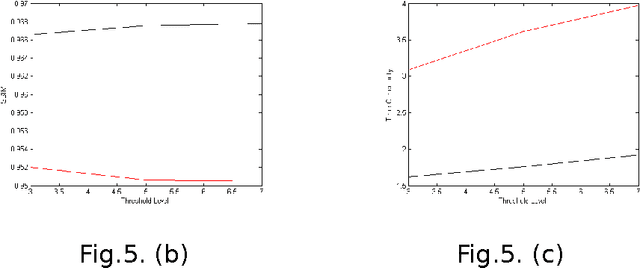
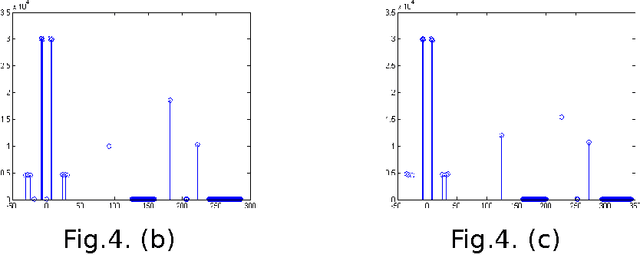
An algorithm is proposed for the segmentation of image into multiple levels using mean and standard deviation in the wavelet domain. The procedure provides for variable size segmentation with bigger block size around the mean, and having smaller blocks at the ends of histogram plot of each horizontal, vertical and diagonal components, while for the approximation component it provides for finer block size around the mean, and larger blocks at the ends of histogram plot coefficients. It is found that the proposed algorithm has significantly less time complexity, achieves superior PSNR and Structural Similarity Measurement Index as compared to similar space domain algorithms[1]. In the process it highlights finer image structures not perceptible in the original image. It is worth emphasizing that after the segmentation only 16 (at threshold level 3) wavelet coefficients captures the significant variation of image.