An Adaptive Statistical Non-uniform Quantizer for Detail Wavelet Components in Lossy JPEG2000 Image Compression

The paper presents a non-uniform quantization method for the Detail components in the JPEG2000 standard. Incorporating the fact that the coefficients lying towards the ends of the histogram plot of each Detail component represent the structural information of an image, the quantization step sizes become smaller at they approach the ends of the histogram plot. The variable quantization step sizes are determined by the actual statistics of the wavelet coefficients. Mean and standard deviation are the two statistical parameters used iteratively to obtain the variable step sizes. Moreover, the mean of the coefficients lying within the step size is chosen as the quantized value, contrary to the deadzone uniform quantizer which selects the midpoint of the quantization step size as the quantized value. The experimental results of the deadzone uniform quantizer and the proposed non-uniform quantizer are objectively compared by using Mean-Squared Error (MSE) and Mean Structural Similarity Index Measure (MSSIM), to evaluate the quantization error and reconstructed image quality, respectively. Subjective analysis of the reconstructed images is also carried out. Through the objective and subjective assessments, it is shown that the non-uniform quantizer performs better than the deadzone uniform quantizer in the perceptual quality of the reconstructed image, especially at low bitrates. More importantly, unlike the deadzone uniform quantizer, the non-uniform quantizer accomplishes better visual quality with a few quantized values.

A Semi-automated Statistical Algorithm for Object Separation

We explicate a semi-automated statistical algorithm for object identification and segregation in both gray scale and color images. The algorithm makes optimal use of the observation that definite objects in an image are typically represented by pixel values having narrow Gaussian distributions about characteristic mean values. Furthermore, for visually distinct objects, the corresponding Gaussian distributions have negligible overlap with each other and hence the Mahalanobis distance between these distributions are large. These statistical facts enable one to sub-divide images into multiple thresholds of variable sizes, each segregating similar objects. The procedure incorporates the sensitivity of human eye to the gray pixel values into the variable threshold size, while mapping the Gaussian distributions into localized \delta-functions, for object separation. The effectiveness of this recursive statistical algorithm is demonstrated using a wide variety of images.

Multisegmentation through wavelets: Comparing the efficacy of Daubechies vs Coiflets

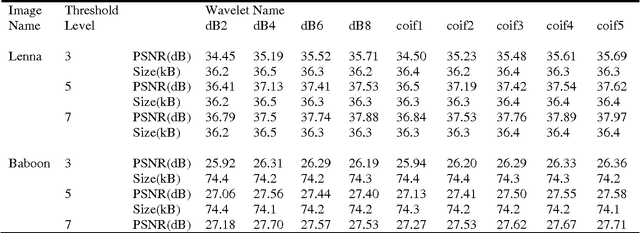
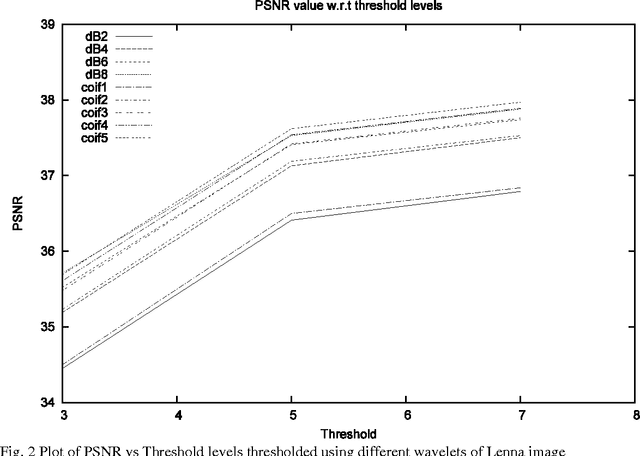
In this paper, we carry out a comparative study of the efficacy of wavelets belonging to Daubechies and Coiflet family in achieving image segmentation through a fast statistical algorithm.The fact that wavelets belonging to Daubechies family optimally capture the polynomial trends and those of Coiflet family satisfy mini-max condition, makes this comparison interesting. In the context of the present algorithm, it is found that the performance of Coiflet wavelets is better, as compared to Daubechies wavelet.