Value-Based Deep Multi-Agent Reinforcement Learning with Dynamic Sparse Training

Deep Multi-agent Reinforcement Learning (MARL) relies on neural networks with numerous parameters in multi-agent scenarios, often incurring substantial computational overhead. Consequently, there is an urgent need to expedite training and enable model compression in MARL. This paper proposes the utilization of dynamic sparse training (DST), a technique proven effective in deep supervised learning tasks, to alleviate the computational burdens in MARL training. However, a direct adoption of DST fails to yield satisfactory MARL agents, leading to breakdowns in value learning within deep sparse value-based MARL models. Motivated by this challenge, we introduce an innovative Multi-Agent Sparse Training (MAST) framework aimed at simultaneously enhancing the reliability of learning targets and the rationality of sample distribution to improve value learning in sparse models. Specifically, MAST incorporates the Soft Mellowmax Operator with a hybrid TD-($\lambda$) schema to establish dependable learning targets. Additionally, it employs a dual replay buffer mechanism to enhance the distribution of training samples. Building upon these aspects, MAST utilizes gradient-based topology evolution to exclusively train multiple MARL agents using sparse networks. Our comprehensive experimental investigation across various value-based MARL algorithms on multiple benchmarks demonstrates, for the first time, significant reductions in redundancy of up to $20\times$ in Floating Point Operations (FLOPs) for both training and inference, with less than $3\%$ performance degradation.

Mixed Sparsity Training: Achieving 4$\times$ FLOP Reduction for Transformer Pretraining

Large language models (LLMs) have made significant strides in complex tasks, yet their widespread adoption is impeded by substantial computational demands. With hundreds of billion parameters, transformer-based LLMs necessitate months of pretraining across a high-end GPU cluster. However, this paper reveals a compelling finding: transformers exhibit considerable redundancy in pretraining computations, which motivates our proposed solution, Mixed Sparsity Training (MST), an efficient pretraining method that can reduce about $75\%$ of Floating Point Operations (FLOPs) while maintaining performance. MST integrates dynamic sparse training (DST) with Sparsity Variation (SV) and Hybrid Sparse Attention (HSA) during pretraining, involving three distinct phases: warm-up, ultra-sparsification, and restoration. The warm-up phase transforms the dense model into a sparse one, and the restoration phase reinstates connections. Throughout these phases, the model is trained with a dynamically evolving sparse topology and an HSA mechanism to maintain performance and minimize training FLOPs concurrently. Our experiment on GPT-2 showcases a FLOP reduction of $4\times$ without compromising performance.

Provably Efficient Iterated CVaR Reinforcement Learning with Function Approximation

Risk-sensitive reinforcement learning (RL) aims to optimize policies that balance the expected reward and risk. In this paper, we investigate a novel risk-sensitive RL formulation with an Iterated Conditional Value-at-Risk (CVaR) objective under linear and general function approximations. This new formulation, named ICVaR-RL with function approximation, provides a principled way to guarantee safety at each decision step. For ICVaR-RL with linear function approximation, we propose a computationally efficient algorithm ICVaR-L, which achieves an $\widetilde{O}(\sqrt{\alpha^{-(H+1)}(d^2H^4+dH^6)K})$ regret, where $\alpha$ is the risk level, $d$ is the dimension of state-action features, $H$ is the length of each episode, and $K$ is the number of episodes. We also establish a matching lower bound $\Omega(\sqrt{\alpha^{-(H-1)}d^2K})$ to validate the optimality of ICVaR-L with respect to $d$ and $K$. For ICVaR-RL with general function approximation, we propose algorithm ICVaR-G, which achieves an $\widetilde{O}(\sqrt{\alpha^{-(H+1)}DH^4K})$ regret, where $D$ is a dimensional parameter that depends on the eluder dimension and covering number. Furthermore, our analysis provides several novel techniques for risk-sensitive RL, including an efficient approximation of the CVaR operator, a new ridge regression with CVaR-adapted features, and a refined elliptical potential lemma.

Effective Multi-User Delay-Constrained Scheduling with Deep Recurrent Reinforcement Learning

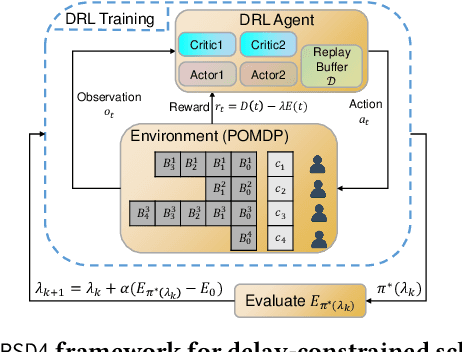
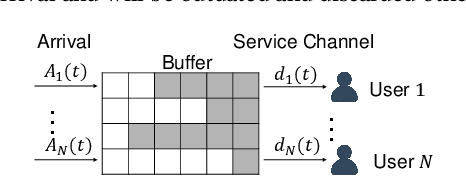
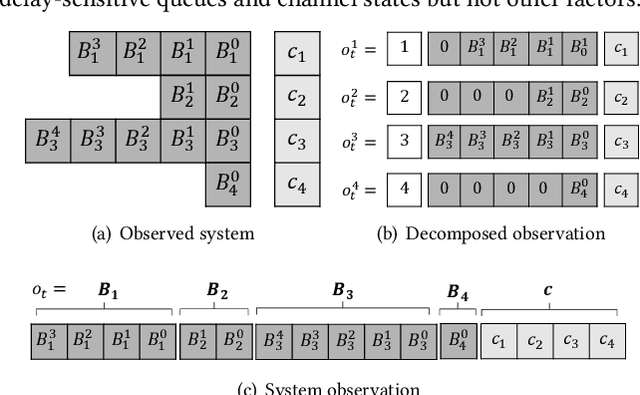
Multi-user delay constrained scheduling is important in many real-world applications including wireless communication, live streaming, and cloud computing. Yet, it poses a critical challenge since the scheduler needs to make real-time decisions to guarantee the delay and resource constraints simultaneously without prior information of system dynamics, which can be time-varying and hard to estimate. Moreover, many practical scenarios suffer from partial observability issues, e.g., due to sensing noise or hidden correlation. To tackle these challenges, we propose a deep reinforcement learning (DRL) algorithm, named Recurrent Softmax Delayed Deep Double Deterministic Policy Gradient ($\mathtt{RSD4}$), which is a data-driven method based on a Partially Observed Markov Decision Process (POMDP) formulation. $\mathtt{RSD4}$ guarantees resource and delay constraints by Lagrangian dual and delay-sensitive queues, respectively. It also efficiently tackles partial observability with a memory mechanism enabled by the recurrent neural network (RNN) and introduces user-level decomposition and node-level merging to ensure scalability. Extensive experiments on simulated/real-world datasets demonstrate that $\mathtt{RSD4}$ is robust to system dynamics and partially observable environments, and achieves superior performances over existing DRL and non-DRL-based methods.

Nearly Minimax Optimal Reinforcement Learning with Linear Function Approximation

We study reinforcement learning with linear function approximation where the transition probability and reward functions are linear with respect to a feature mapping $\boldsymbol{\phi}(s,a)$. Specifically, we consider the episodic inhomogeneous linear Markov Decision Process (MDP), and propose a novel computation-efficient algorithm, LSVI-UCB$^+$, which achieves an $\widetilde{O}(Hd\sqrt{T})$ regret bound where $H$ is the episode length, $d$ is the feature dimension, and $T$ is the number of steps. LSVI-UCB$^+$ builds on weighted ridge regression and upper confidence value iteration with a Bernstein-type exploration bonus. Our statistical results are obtained with novel analytical tools, including a new Bernstein self-normalized bound with conservatism on elliptical potentials, and refined analysis of the correction term. To the best of our knowledge, this is the first minimax optimal algorithm for linear MDPs up to logarithmic factors, which closes the $\sqrt{Hd}$ gap between the best known upper bound of $\widetilde{O}(\sqrt{H^3d^3T})$ in \cite{jin2020provably} and lower bound of $\Omega(Hd\sqrt{T})$ for linear MDPs.

RLx2: Training a Sparse Deep Reinforcement Learning Model from Scratch

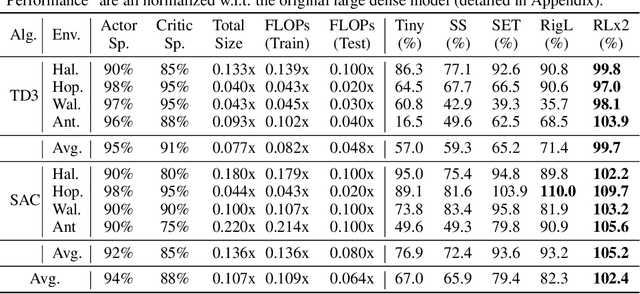
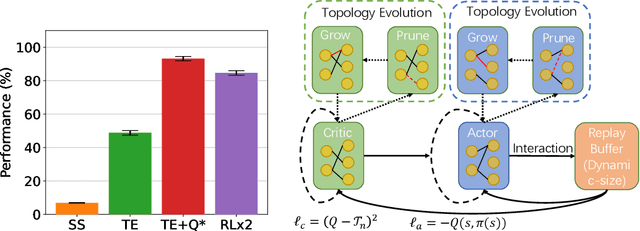
Training deep reinforcement learning (DRL) models usually requires high computation costs. Therefore, compressing DRL models possesses immense potential for training acceleration and model deployment. However, existing methods that generate small models mainly adopt the knowledge distillation based approach by iteratively training a dense network, such that the training process still demands massive computing resources. Indeed, sparse training from scratch in DRL has not been well explored and is particularly challenging due to non-stationarity in bootstrap training. In this work, we propose a novel sparse DRL training framework, "the \textbf{R}igged \textbf{R}einforcement \textbf{L}earning \textbf{L}ottery" (RLx2), which is capable of training a DRL agent \emph{using an ultra-sparse network throughout} for off-policy reinforcement learning. The systematic RLx2 framework contains three key components: gradient-based topology evolution, multi-step Temporal Difference (TD) targets, and dynamic-capacity replay buffer. RLx2 enables efficient topology exploration and robust Q-value estimation simultaneously. We demonstrate state-of-the-art sparse training performance in several continuous control tasks using RLx2, showing $7.5\times$-$20\times$ model compression with less than $3\%$ performance degradation, and up to $20\times$ and $50\times$ FLOPs reduction for training and inference, respectively.